反馈控制系统理论中运用了全状态反馈的概念,使配置系统的所有闭环节点成为可能。极点对应于系统的动态行为,因此将它们配置在一个期望的位置可能非常有趣。在 COMSOL Multiphysics® 软件中,我们可以使用状态空间控制器插件为系统模型添加一个全状态空间反馈控制器。这篇博客,我们简要回顾了全状态反馈,描述了如何使用该插件,并演示一个示例。
关于全状态反馈
全状态反馈假设系统的闭环动力学在形式上可以表示为
如果 \boldsymbol{D} = 0,只要系统是可控 的,我们就可以通过求解特征方程来任意配置系统的极点。
使用插件实现状态空间反馈控制器
使用插件,我们能够在模型中实现一些功能。从 5.6 版本开始,COMSOL Multiphysics 提供了一个状态空间控制器插件,可以配置闭环系统的极点。
有关控制器插件的另一个示例,请参阅博客文章:如何使用 PID 控制器插件模拟控制系统。
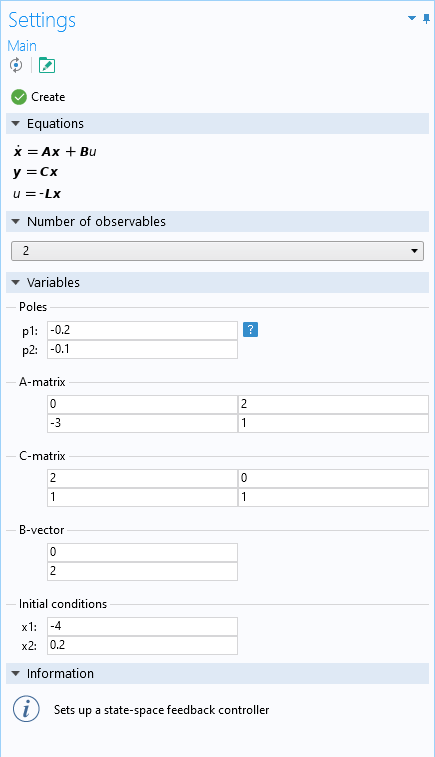
状态空间控制器插件的 设置窗口。
我们可以先定义所需系统的观测变量的数量,矩阵 \boldsymbol{A} 和 \boldsymbol{C},矢量 \boldsymbol{B},初始条件,以及在复平面中配置极点的位置。然后使用插件创建一个新的零维模型组件,该组件使用全局方程 定义反馈控制器。信息 部分提到了相关的组件,以及创建控制器后如何访问输出变量。控制变量可以用作 u。
下面介绍一个如何使用插件的示例。
力对双质量-阻尼-弹簧的示例
以一个描述质量为 m_{1} 的质点的系统为例, 一侧连接到带有弹簧和阻尼器的墙壁上,另一侧用弹簧和阻尼器连接到第二个质量为 m_{2} 的质点。第二个质量点又受到一个力 F 的作用,为了达到平衡,这个力需要被控制。
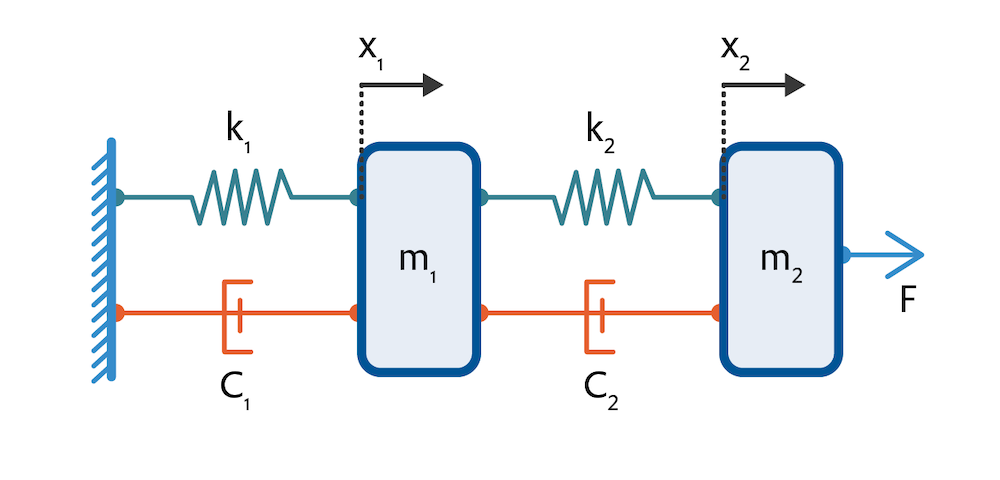
该系统由以下方程描述,这些方程是牛顿第二运动定律的实例,使用点符号表示时间导数:
式中,k_{1} 和 k{2} 是两个弹簧的弹簧常数,c_{1} 和 c_{2} 是两个阻尼器的阻尼常数,\tilde{x}_{1} 和 \tilde{x}_{2} 用于描述两个质点与其各自平衡位置的偏差。
引入四个新变量,x_{1}=\tilde{x}_{1}, \, x_{2}=\dot{\tilde{x}}_{1}, \, x_{3}=\tilde{x}_{2}, 和 x_{4}=\dot{\tilde{x}}_{2},我们得到一个系统形式为
其中,
0 & 1 & 0 & 0\\
-(k_{1}+k_{2})/m_{1}& -(c_{1}+c_{2})/m_{1} & k_{2}/m_{1} & c_{2}/m_{1}\\
0 & 0 & 0 & 1\\
k_{2}/m_{2} & c_{2}/m_{2} & -k_{2}/m_{2} & -c_{2}/m_{2}
\end{pmatrix} \text{ 和 } \boldsymbol{B} = \begin{pmatrix}
0 \\
0\\
0\\
1/m_{2}
\end{pmatrix}.
在这种情况下,控制变量 u,F 是力,\boldsymbol{C} 是单位矩阵。我们将常量定义为参数,如下所示。
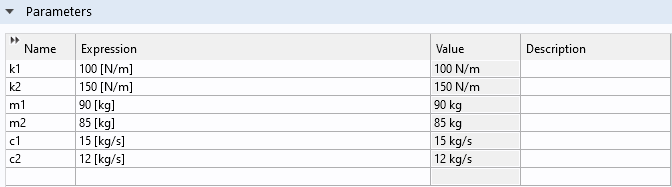
常量的定义。
我们现在可以使用状态空间控制器插件来配置闭环系统的极点。假设我们想要四个实极点,都为-0.5。由于我们有四个可观察量,设置如下所示的插件。
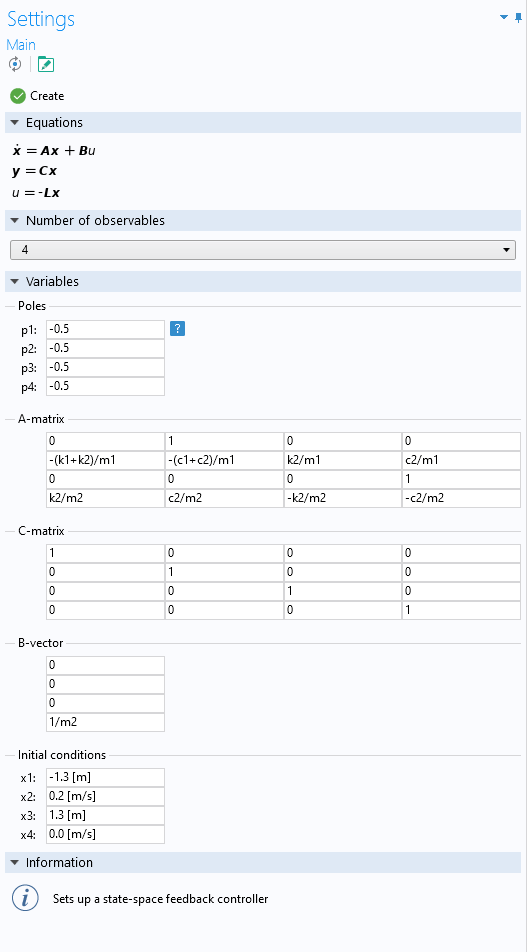
双质量阻尼器系统的状态空间控制器设置。
选择初始条件,使得第一个质量块开始于负 x 方向 1.3 m,速度为 0.2 m/s,第二个质量块从静止开始,从它的平衡点向正 x 方向 1.3 m。
单击创建 后,会收到以下消息。
状态空间控制的输出变量的描述。
现在,我们可以运行研究,假设质量点在平衡状态下相距 3 米,我们可以绘制变量 y1 和 y3+3,以看到它们位置的时间演变。因为 y1 和 y3 是两个质量点的平衡位置的距离,所以当两个质量点相距 3 米时,质量 2 与质量 1 的平衡位置的距离是 y3+3。
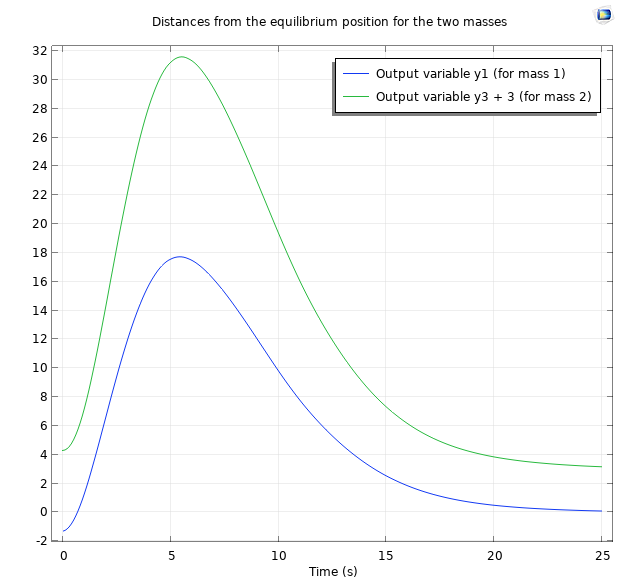
前 25 s 内两个质量点的位置,此时所有极点都位于 -0.5。
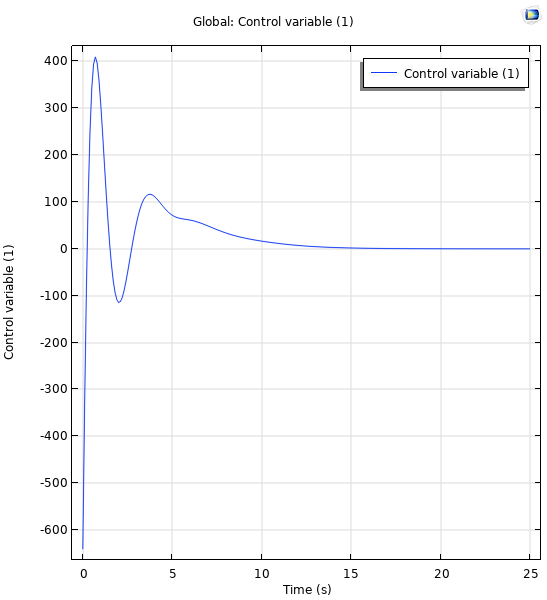
我们还可以绘制作用力,它可以通过控制变量 u 访问,得到以下绘图。
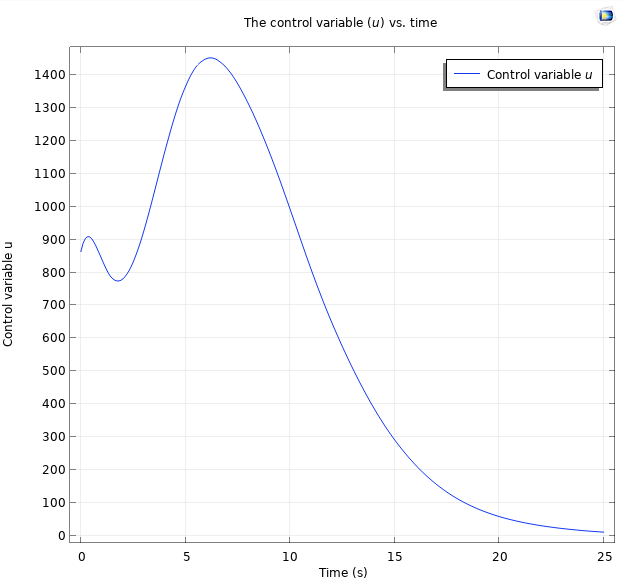
在模拟的前 25 s绘制控制变量,此时所有极点都位于 -0.5。
假设我们对上述系统的稳定时间不满意。从控制理论来看,如果我们将极点进一步配置在负实平面中,预计稳定时间会减少。如果我们按照上面的程序,将所有极点配置在-1 而不是 -0.5,就可以获得下面的位置图。
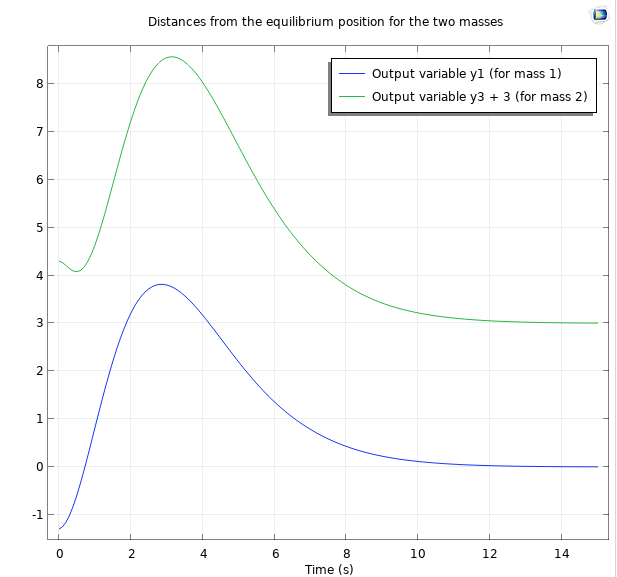
前 15s 的位置图,此时所有极点都位于 -1。
此外,我们还可以得到如下所示的受控力图。
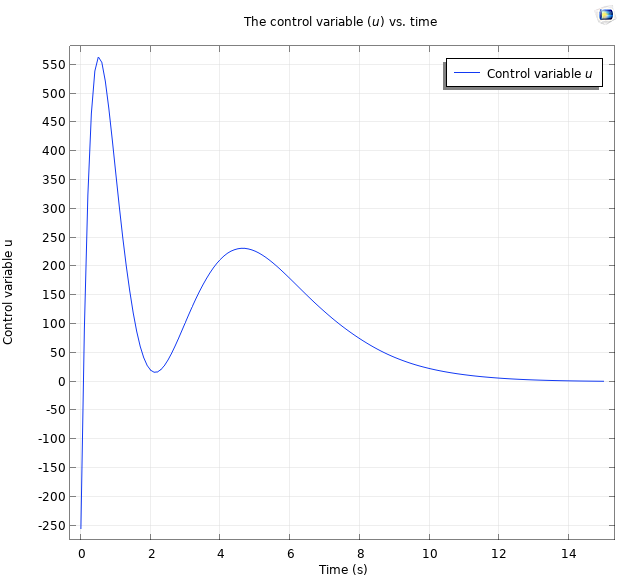
前 15 s 的受控力图,此时所有极点都位于 -1。
正如预期的那样,系统稳定得更快。
在状态空间控制器插件中,还可以在复平面中配置极点。复极点总是以复共轭对的形式出现。
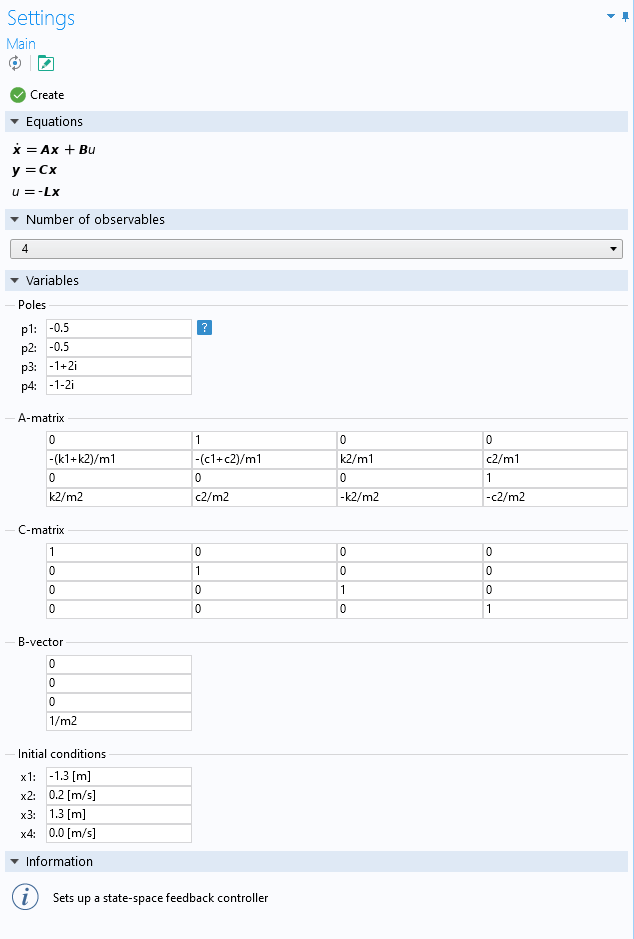
具有两个复极点的状态空间控制器设置。
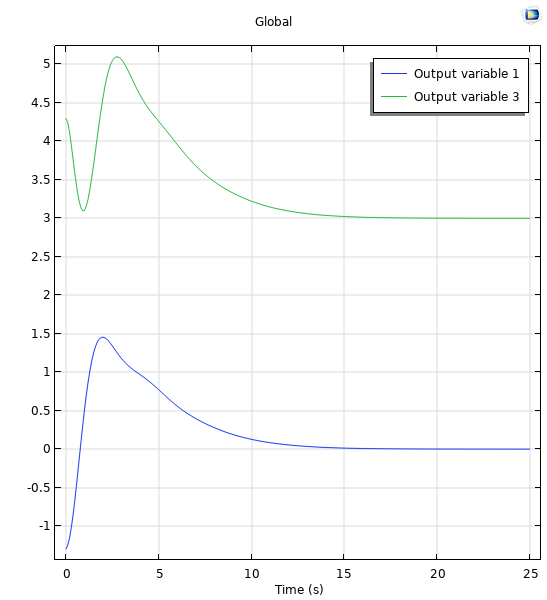
这个结果会产生如下图所示的位置和控制信号图。
两个实极点分别位于 -0.5 和两个复极点位于 -1+2i 和 -1-2i 的位置图(左)。两个实极点(-0.5)和两个复极点(分别为 -1+2i 和 -1-2i)的控制信号图(右)。
极点配置
从上一节的模拟可以看出,系统的行为会发生巨大变化,具体取决于闭环系统的极点配置的位置。很难找到关于极点配置如何影响任意系统的一般描述。但是,如上所述,可以说配置连续系统的极点应该会使稳定更快,但可能会导致更大的控制信号。使用状态空间控制器插件,您可以轻松评估各种极点配置的系统行为。



评论 (0)