由 Yosuke Mizuyama 创作的所有博客
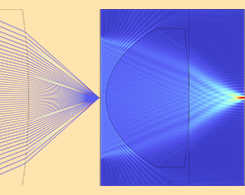
如何使用空间快速傅里叶变换(FFT)模拟光学应用
2022年 8月 19日
COMSOL Multiphysics® 6.0 版本包括新的空间 FFT 特征。了解如何在光学应用中应用该功能。
用于毒理学分析的实用沉降仿真 App
2022年 1月 25日
沉淀作用被广泛用于毒理学、生物化学和生物医学中。你可以通过模拟研究重力如何影响这一物理现象。
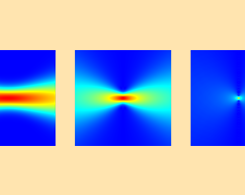
非近轴高斯光束的倏逝分量
2020年 5月 12日
自 COMSOL Multiphysics® 5.5 版本起,非近轴高斯光束背景场的渐逝分量可作为波动光学和射频模块中的一项功能使用。

如何使用波动光学模块模拟透镜
2020年 2月 19日
透镜模拟波动光学中的透镜模拟可能很难执行,因为它们通常需要很多网格元素。了解如何使用波动光学模块的功能回避此问题。

通过仿真理解经典灰体辐射理论
2018年 11月 1日
想象一下带有红外抑制黑体灯丝的白炽灯会有多高效。 经典的灰体辐射理论告诉我们这个“梦灯”是不可能的……

模拟波动光学的非近轴高斯光束公式
2018年 6月 26日
这是您对非近轴高斯光束公式的介绍,该公式用于在 COMSOL Multiphysics® 中模拟波动光学问题。
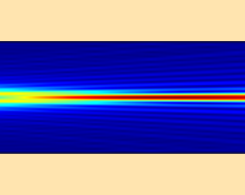
如何使用波束包络法进行波动光学模拟
2018年 1月 8日
模拟大型光学系统以一种严格解决麦克斯韦方程的方式是不容易的,由于精细网格的要求。一种解决方案是采用梁包络法。这是如何。
如何利用多物理场射线追踪分析激光腔的稳定性
2017年 6月 15日
激光是现代科学中最有用的发明之一,但它使用起来并不容易。仅当腔镜完全对准时,激光器才能工作。即使激光发射了一段时间,它也可能突然停止。
