COMSOL 最新动态 博客文章

多物理场仿真和仿真 App 推动创新
了解为什么您的团队应该考虑将最新版本的 COMSOL Multiphysics® 作为您的研发工作流程的一部分。

2025 年仿真技术的发展趋势预测
2025 年 建模与仿真将带来什么?阅读这篇博客,了解我们的 3 个预测。

诞辰快乐!路德维希·玻尔兹曼
路德维希-玻尔兹曼被誉为19世纪最重要的物理学家之一。阅读博客,了解关于他的生活和工作。

最新发布的 COMSOL® 6.1 版本有哪些新功能?
COMSOL Multiphysics® 6.1版本引入了分离涡流模拟、卫星热分析、强大的机械接触建模等新功能。
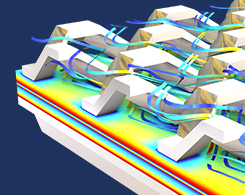
COMSOL Multiphysics® 6.0 版本全新发布
COMSOL Multiphysics® 6.0 版引入了模型管理器、不确定性量化模块以及整个产品库中的许多重要更新。
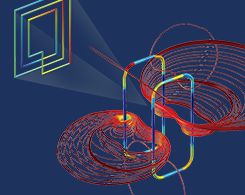
仿真在生物医药行业的应用日益增长
从植入物和支架到核磁共振成像和脊髓刺激,数值建模对于生物医学设备的开发至关重要。了解更多信息,并聆听该行业主要参与者的发言。

借助仿真实现声呐系统的快速原型设计
借助多物理场仿真技术,诺斯罗普·格鲁曼公司(Northrop Grumman Corporation,NGC)快速完成了声呐系统的创新设计和实现。Lauren Lagua 是 NGC 水下系统部门声呐集成团队成员之一,她在 2020 年北美 COMSOL 用户年会的主题演讲中,讨论了如何使用 COMSOL Multiphysics® 软件在声呐系统开发中进行快速原型设计。文中摘录了她的一些演讲内容,并附加了完整的视频演讲,欢迎浏览。 视频演讲:NGC 如何使用 COMSOL Multiphysics® 进行快速原型设计 NGC 的快速原型设计流程 在 NGC 公司,工程师遵循着快速原型设计的流程,该流程包括四个部分,其中前三个部分经常重复多次: 原型设计 原型制造 测试与设计验证 最终设计的制造 Lauren Lagua表示,在该流程的每一个环节都使用了多物理场仿真技术。 原型设计 在为声呐系统设计换能器(Tonpilz 型压电换能器案例模型)时,工程师会通过测试不同的参数设置,来了解如何最好地实现项目的总体目标。他们可能会尝试测试材料(例如新的压电材料)、几何形状和频率等参数。Lauren 团队使用 COMSOL Multiphysics 的 压力声学、固体力学、静电 和电路 接口,确定了不同的参数变化如何影响其设计。 在测试新材料时,团队经常缺少供应商提供有关材料属性的所有必要信息。因此,他们使用 COMSOL Multiphysics 评估已有信息测试材料属性,并将评估结果与 COMSOL 模型进行比较来估计材料性质。 主题演讲的屏幕截图,显示了换能器设计中使用的材料。 原型制造 NGC 团队在建立好模型并运行之后,会在整个原型制造过程中执行一系列测试,并将其与模拟结果进行比较。有时结果会不匹配,例如模型中可能缺少物理场。有时,Lagua能够在原型中发现制造问题。例如,当将压电材料黏合到背衬基板时,可能会出现气泡或黏合不良等问题。 Lagua 对导致问题的原因进行了假设,并在 COMSOL Multiphysics 中模拟了其假设。通过将模型结果与原始原型的假设进行比较,Lagua 能够快速对制造问题进行故障排除并纠正。 测试和验证 准备好原型后,NGC 团队将对其电气和声学特性进行系统级测试。 电气测试包括阻抗测试和电容测量。 在声学方面,NGC 公司使用了最先进的声学测试设备。该设备是私营企业最大的测试池,直径为 15 米,可容纳约 1500 立方米水,并用红木衬砌,以建造一个理想的宽带声学测试环境(模仿开放水域环境)。声学测试池用于测量声呐换能器中的发射电压响应,远场电压灵敏度和辐射方向图。该设备的测试结果将被反馈回模型中,并进行验证模型,或者在必要时进行调整。 声学测试池。图片由 Northrop Grumman Corporation 提供。 一旦设计通过了快速原型设计流程的前三个阶段,就可以一次又一次地快速迭代它们,直到准备好制造出最终设计版本为止。 微型无人水下飞行器的声呐 在 Lagua 的主题演讲中,她以 NGC 公司的一个项目为例说明了如何借助仿真快速实现声呐系统的原型制造。该项目成功使用 COMSOL […]
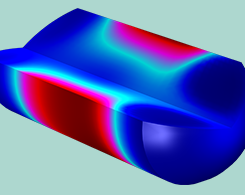
在药物研发过程中越来越多地使用仿真
通常,药物的研发周期可能需要数年时间,花费数百万美元。但是,通过模拟和仿真,这个过程可以变得更快和更具成本效益。认识到了这些好处,美国食品药品监督管理局(FDA)和世界各地的学术制药项目都不约而同地选择了模拟和仿真。阅读这篇博客文章,您可以了解到如何在药物研发中进行模拟,并查看一些具体示例。
