在 COMSOL Multiphysics® 软件中求解一个模型后，我们可能希望将解数据拟合到在仿真域中定义的一组函数中。在之前的博客中，我们解释了如何将离散试验数据拟合为曲线。今天，我们将考虑对连续的解数据进行拟合。然后，我们将介绍正交性的概念，并解释如何将解数据拟合到一组正交函数中，从而简化为一种简单、方便的后处理操作。
曲线拟合的好处
在上一篇关于拟合离散试验数据的博客文章中，我们解释了如何将曲线拟合用于随后的仿真工作。例如，如果我们使用原始实验数据直接定义材料属性，那么数据中的统计波动会使求解器更难以收敛。此外，将离散数据拟合到平滑函数可以获得该函数的高阶导数，而尝试对原始数据进行数值微分可能会产生很大干扰，并且容易出错。
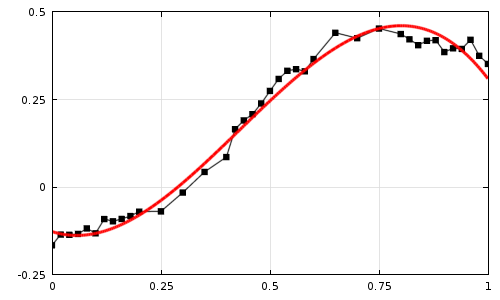
将原始实验数据(黑点)拟合为三次多项式(红色曲线)。
对 COMSOL Multiphysics® 模型中之前研究的解数据进行曲线拟合，会怎么样？一个直接的好处就是数据压缩。如果我们可以找到与完整解具有良好一致性的线性函数组合，就可以通过共享几个函数系数的值描述来自完整解的大部分信息。（请注意，对于数据压缩，没有放之四海而皆准的方法；在 COMSOL 知识库中，减少模型中存储的解数据量一文介绍了其他几种方法，例如使用探针表和选择）。
此外，对连续解数据进行曲线拟合可以方便地估计解的高阶空间导数。COMSOL® 软件中的许多物理场接口使用了由分段拉格朗日多项式组成的有限元离散化，默认情况下，这些多项式通常是二阶的。在这种情况下，导数不一定是连续的，三阶或高阶导数总是零。
最小二乘拟合概述
首先，我们来了解一下简单最小二乘拟合的基本数学原理。在用 Ω 表示的某个模拟域（或边界或边）中，假设COMSOL Multiphysics® 模型已经求解了场变量 u。我们的目标是通过将其视为一组预定义函数的线性组合来近似 u 在该域上的值，
其中，fi 是一组已知函数，ci 是必须求解的系数。
确定这些未知系数的常用方法，是求 u 和它的近似值之差 L2 范数，
然后，找到对应于这个 L2 范数的局部最小值的ci。
在 Ω 内的局部极小值处，未知系数的导数必须等于零，
这里，我们使用下标 j 来避免与求和符号混淆。
假设积分号下的所有函数都可导，应用链式法则可以将它简化
约掉系数 2，交换积分和离散求和的顺序，得到
最终得到的结果是一组有 N 个系数未知的 N 维线性方程组。例如，如果有三个多项式，就可以把这个结果写成矩阵形式，
&\begin{bmatrix}
A_{11} & A_{12} & A_{13}\\
A_{21} & A_{22} & A_{23}\\
A_{31} & A_{32} & A_{33}
\end{bmatrix}
\begin{bmatrix}
c_1\\
c_2\\
c_3
\end{bmatrix}
=
\begin{bmatrix}
B_1\\B_2\\B_3\\
\end{bmatrix}\\
&A_{ij} \equiv \int_\Omega f_i(\mathbf{r})f_j(\mathbf{r})\textrm{d}\Omega
\qquad B_{j} \equiv \int_\Omega u(\mathbf{r})f_j(\mathbf{r})\textrm{d}\Omega
\end{aligned}
因此，求解这个方程组的未知系数需要计算 N(N+3)/2 次积分(注意左边的矩阵是对称的，即 fifj 的积分等于 fifj 的积分)和一组 N 个线性代数方程的解。
在下一节我们将看到，如果定义相应的函数 fi，使它们在我们尝试拟合解数据的区域中正交，那么系数c i 的计算就会大大简化。
正交函数简介
在讨论正交性的概念时，必须注意给出的定义不要过于狭窄。一般而言，如果 \langle u,v\rangle=0，属于一个向量空间的两个不同向量， u 和 v 在内积 \langle u,v\rangle 下是正交的，那么内积的确切定义可以根据向量空间而改变。
由于我们讨论的是在 n 维实坐标空间(\mathbf{r}\in\mathbb{R}^n)的某个区域 Ω 上，一个空间变化的解向量对一组函数 f1(r)，f2(r)，…fN(r) 的曲线拟合，因此可以得到更具体的表达式，并将这些函数的内积定义为
式中，w(r) 为某个尚未定义的权函数，对于 Ω 中的所有 r，限制为：w(r) > 0。
例如，f_1(x) = 1，f_2(x) = \sin x 和 f_3(x) = \cos x 在内积下正交。
也就是说，Ω 的区域是一维区间 x\in[-\pi,\pi]，权函数可以简单的表示为 w(x)=1。我们可以通过计算下列积分来证明这些函数的正交性
\int_{-\pi}^\pi (1)^2 \textrm{d}x &= 2\pi \qquad \int_{-\pi}^\pi (\sin x)^2 \textrm{d}x = \pi \qquad \int_{-\pi}^\pi (\cos x)^2 \textrm{d}x = \pi \\
\int_{-\pi}^\pi (1)(\sin x) \textrm{d}x &= 0 \qquad \int_{-\pi}^\pi (1)(\cos x) \textrm{d}x = 0 \qquad\int_{-\pi}^\pi (\sin x)(\cos x) \textrm{d}x = 0\\
\end{aligned}
事实上，我们可以进一步扩展这个概念，并将看到函数 sin(2x)，cos(2x)，sin(3x)，cos(3x) 等在同一个内积下也是正交的。这些三角函数的正交性是傅立叶级数展开的基础。
正交函数的最小二乘拟合
现在，让我们利用对正交函数的了解，重新审视线性最小二乘拟合问题，正如我们之前所看到的，该问题将简化为求解系数 ci 的集合，使得
现在，假设函数 fi 都是在内积下是正交的
你可能已经注意到了一些技巧：在谈到 n 维向量空间的内积时，我们在内积的定义中使用了微分元 dΩ，但是 dΩ 将根据我们选择的坐标系（如笛卡尔坐标系、圆柱极坐标系、球极坐标系等）而采用不同的表达形式。我们在后面的示例中也将看到，为了最大程度的方便，我们可以选择一组在内积下正交的函数，其权函数等于所用坐标系的雅可比行列式。
由于函数的正交性，所有的非对角线项在 N \times N 矩阵的左边消失了，N 个方程组现在只是一组 N 个表达式的集合，可以直接得到 ci 的值
如果选择将这些函数规一化，以使上述表达式的分母为 1，我们就会得到看起来更简单的表达式
因此，将解数据拟合到一组 N 个函数的任务已经简化为计算 N 个不同的积分。在 COMSOL® 软件中，我们可以轻松定义积分 耦合，来计算在任何区域、边界、边或几何点集合的积分。(我们甚至不需要在定义积分 耦合后重新运行研究，只需单击更新解即可。)
在接下来的部分，我们将研究一个更真实的示例: 将镜子的变形拟合到一组 Zernike 多项式。
泽尼克多项式
光学中最常用的一个正交函数是泽尼克多项式，它是圆的径向坐标和平面角的函数，
式中，
- ρ 是径向坐标(0\leq\rho\leq 1)
- θ 是方位角 (0\leq \theta < 2\pi)
- N_n^m 是归一化项
- R_n^{|m|}(\rho) 是径向项
- M(m\theta) 是子午项或方位项
- n 是径向指数 (n \in \left\{0,1,2,\dots\right\})
- m 是子午线或方位角指数（对于给定的 n，m \in \left\{-n, -n+2, -n+4, \dots , n-2, n\right\})
需要注意的是，对于如何定义泽尼克多项式以及如何解释其指数，有几种不同的标准格式。COMSOL Multiphysics® 中使用的函数定义使用两个独立的指数来描述函数的径向和方位角相关性，符合 ANSI 和 ISO 标准（参考文献 1、2）。泽尼克多项式通常是针对单位圆定义的，但可以通过将 ρ 替换为 ρR （尽管这会影响归一化）来定义任何其他半径为 R 的圆。
下面列出了部分泽尼克多项式。
| 项 | 表达式 | 通用名 |
|---|---|---|
| Z_0^0 | 1 | 平移 |
| Z_1^{-1} | 2\rho \sin(\theta) | 垂直倾斜 |
| Z_1^1 | 2\rho \cos(\theta) | 水平倾斜 |
| Z_2^{-2} | \sqrt{6}\rho^2 \sin(2\theta) | 斜散像差 |
| Z_2^0 | \sqrt{3}\left(2\rho^2-1\right) | 散焦 |
| Z_2^2 | \sqrt{6}\rho^2 \cos(2\theta) | 垂直散光 |
| Z_3^{-3} | \sqrt{8}\rho^3 \sin(3\theta) | 斜三叶像差 |
| Z_3^{-1} | \sqrt{8}\left(3\rho^3-2\rho\right)\sin(\theta) | 垂直慧差 |
| Z_3^1 | \sqrt{8}\left(3\rho^3-2\rho\right)\cos(\theta) | 水平慧差 |
| Z_3^3 | \sqrt{8}\rho^3 \cos(3\theta) | 水平三叶像差 |
| Z_4^{-4} | \sqrt{10}\rho^4\sin(4\theta) | 斜四叶像差 |
| Z_4^{-2} | \sqrt{10}\left(4\rho^4-3\rho^2\right)\sin(2\theta) | 斜次阶散光像差 |
| Z_4^0 | \sqrt{5}\left(6\rho^4-6\rho^2+1\right) | 初阶球差 |
| Z_4^2 | \sqrt{10}\left(4\rho^4-3\rho^2\right)\cos(2\theta) | 垂直次阶散光像差 |
| Z_4^4 | \sqrt{10}\rho^4\cos(4\theta) | 水平四叶像差 |
选择归一化项，以使
如果两个下标相等，则 Kronecker delta δ 等于 1，否则为 0。
与我们之前的术语保持一致，泽尼克多项式在权函数 w(\rho,\theta)=\rho 下的单位圆上是正交的。在笛卡尔坐标和圆柱极坐标 \textrm{d}\Omega = \rho\textrm{d}\rho\textrm{d}\theta 之间转换时，权函数 ρ 可以很方便的与雅可比行列式完全匹配。
泽尼克多项式广泛用于光学领域。如果你曾经拜访过眼科医生，那么可能听说过“散光”(Z_2^{\pm 2})或“慧差”(Z_3^{\pm 1})之类的术语，而“近视”和“老花眼”只是“散焦”（Z_2^0）的不同表述。
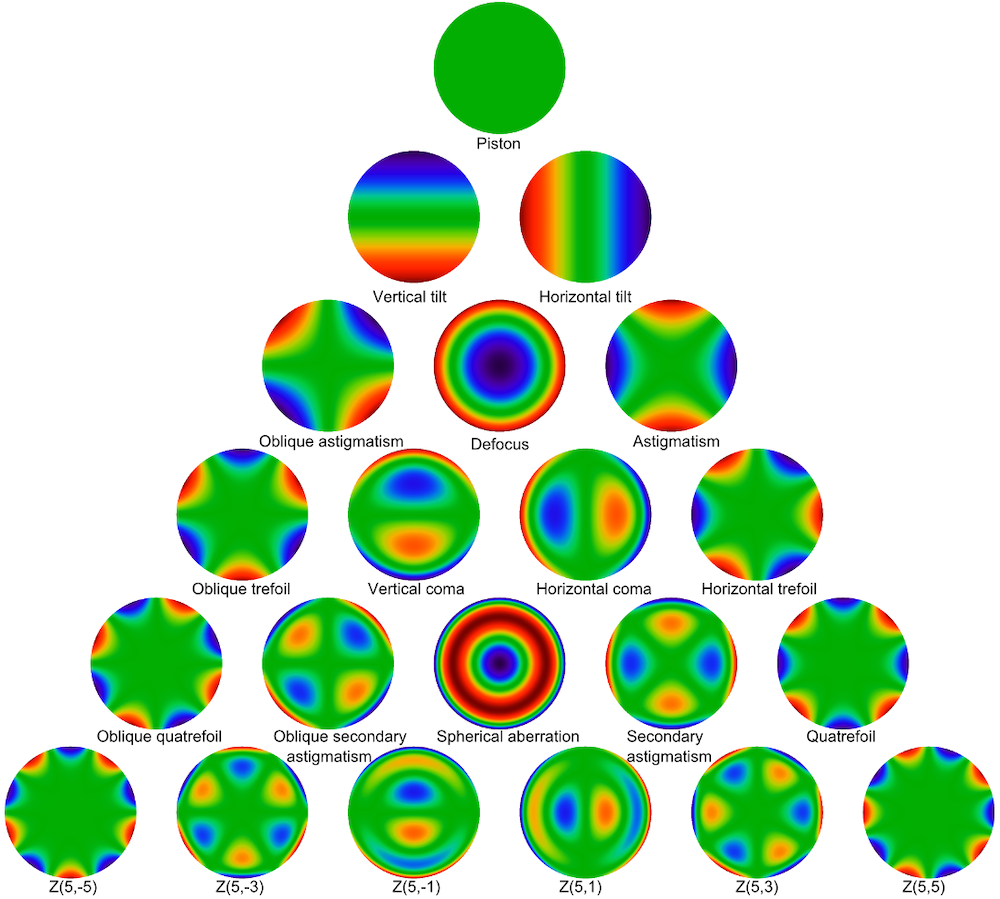
高达五阶的泽尼克多项式图。
用泽尼克多项式表示变形镜
最后，让我们用所学的知识来做一个例题。示例中的几何体是一个侧面和底部固定的平面柱面镜，上表面可以自由变形。透镜被均匀加热后产生热应力，并导致镜面的表面膨胀。
未变形镜(左)和变形镜(右)的几何形状。
我们希望计算最适合拟合变形表面镜位移场的泽尼克多项式系数。如以下屏幕截图所示，为了完整起见，我们将包括所有四阶泽尼克多项式，尽管只有径向指数为 0 的项（平移 Z_0^0，散焦 Z_2^0 和球差 Z_4^0) 由于位移场的对称性而发挥了重要作用。为了对位移与每个泽尼克多项式的乘积进行积分，在变形表面上定义了一个积分 耦合。然后使用一些变量 节点来定义每个泽尼克多项式与解向量的乘积的积分，从而确定相应的泽尼克系数的值。
最后，我们绘制出位移场 w 在从镜面中心向外径向延伸的切线上的面外分量，并将其与泽尼克多项式的线性组合进行了比较。下图显示了平移、散焦和球差的单独组合，并将它们的线性组合与位移场进行了比较。可以看出，解与泽尼克多项式拟合的一致性相当好，并且可以通过引入高阶项(如 Z_6^0)进一步优化。
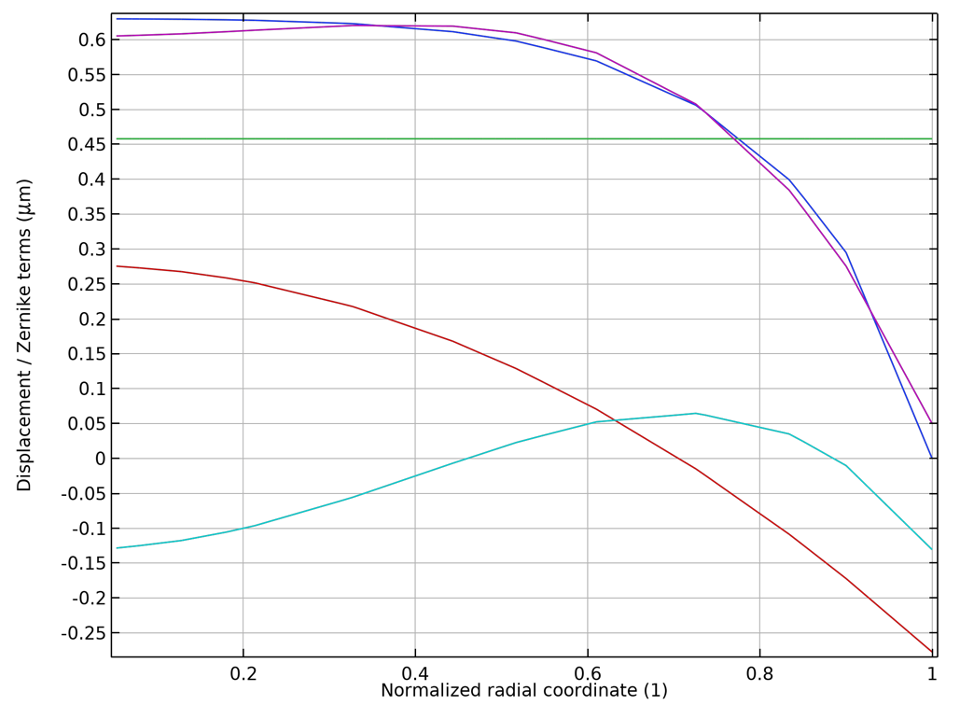
位移场(蓝色)与泽尼克多项式拟合(紫色)的比较。分别显示了平移(绿色)，散焦(红色)和球差(青色)。
结论
曲线拟合是一种消除实验数据中的统计噪声的工具，它也可以应用到模型求解本身，并且效果很好。将解数据拟合到一组预定义函数，尤其是正交函数中，提供了一种快速、方便的数据压缩方法。
下一步
点击下方按钮，进入 COMSOL 案例下载页面下载示例的mph 文件，尝试自己动手模拟这篇博客中讨论的模型。
参考文献
- ISO 24157:2008: Ophthalmic optics and instruments — Reporting aberrations of the human eye, International Organization for Standardization, Geneva, Switzerland. Amendment 1, ibid., 2019.
- ANSI Z80.28-2017: American National Standard for Ophthalmics — Methods of Reporting Optical Aberrations of Eyes. American National Standards Institute, Alexandria, VA.
评论 (2)
tx 孙
2021-10-12请问如何在绘图组中导出空间间距一致的二维/三维绘图数据呢
洋洋 张
2021-10-20 COMSOL 员工右键点击“结果”-“导出”，添加“数据”子节点，在“要计算的点”里选择栅格或“规则栅格”，定义您想要导出的数据坐标即可。