如果锂离子电池的电极平衡不正确,则电池开路电压将不会准确。在本篇博客文章中,我们将介绍电极中的物质守衡以及其是如何产生的,并使用 COMSOL Multiphysics® 软件演示了一个简易电池模型。 通过该模型中使用的方法可以使电极实现平衡。此外,我们还将讨论如何将该方法用于高级建模,例如预测不同速率的充放电倍率容量并分析与电位相关的老化问题。
为什么电极平衡很重要?
电池单元由一个负极(放电过程中的阳极)和一个正极(放电过程中的阴极)组成。另外,在锂电池中,阴极上还原的锂离子的量必须等于阳极上氧化的锂原子的量。在电池工程中,平衡两侧的活性电极材料的数量至关重要。一种材料过多意味着有效地增加了电池的自重,因为如果另一种材料不能适当地平衡,则不可能 100% 的利用该电极的活性物质。

将电池充电和放电视为在两个杯子(电极)之间来回倒入能量饮料(锂)。鉴于一开始必须先装满一个玻璃杯(平整的),如何选择每个玻璃杯的尺寸以最大程度地减少容器的总体积,同时又要最大程度地增加倒出的液体的数量(容量)和流量(流量),而不会溢出(电池老化)?
在建模方面(对于同时定义正极和负极的任何模型),电极平衡具有重要意义,因为除非适当的平衡,否则电池模型的开路电势将是不正确的。(此外,如果您的开路电势不正确,这意味着您的模型甚至在未通电流时都是不准确的。)
下面从工程角度出发,讨论如何为特定容量的电池设计电极平衡。在此讨论中,我们将使用以下定义:
- 标准电池容量:在一定的充电/放电速率下,一组指定最大和最小电压限制的电池容量
- 宿主电池容量:每个电极中可以存储锂的位点数量
- 可循环锂:在循环过程中可从电极添加或去除的可循环锂原子的数量(两个电极的总和)
电极平衡理论
正极上的可循环锂
负极(石墨、钛酸盐、硅等)材料在制造时不含锂,或未完全锂化;而正极材料(锂金属氧化物,磷酸锂等)已完全锂化。因此,原始可循环锂的量等于正极的主体容量。最初的电极平衡方法是在正极上添加所需数量的电极材料,以达到电池的标称容量,并在负极上添加相应数量的电极材料。但是,这并不容易。
选择正极容量
在正电极上,高电势可能导致不可逆的电解质氧化和气体形成,或金属离子从氧化锂基体中溶解,完全脱锂也可能破坏基体。为了延长使用寿命(或为了安全起见),电池工程师必须指定最大电极电压。
本质上,该最大值意味着降低正极的允许锂化窗口,即在电池中必须使用比标准电池容量更多的正极活性材料(建模是评估各种充电倍率下电极中电势水平的绝佳工具,但这不是本篇博客文章的研究范围)。因为在正常操作范围内,只能允许利用一部分正极容量。因此,我们不能仅基于标称电池容量研究电极平衡,我们还需要考虑对负极的有害循环效应。
增加多余的负容量
在充电即将结束时,负极达到其最低电位。负极处的低电势对电池有害,因为这可能会加速固体电解质膜(SEI)的形成,电极电势开始接近锂金属电镀的电位。
如果在电池中发生锂金属镀层,则可能导致可循环锂的额外损失,并且还导致锂金属枝晶的生长,枝晶使电池存在短路的风险。此外,由于在接近完全锂化时电极的体积膨胀系数增加,导致低电位石墨制成电极存在机械破坏问题。
较大电充电流下产生的不均匀电流分布,会进一步加剧低电位及接近100%锂化的风险(建模可以帮助评估)。因此,相对于普通电池的标准容量,负极理论容量需要适当增加。但是,这也会是事情变得更加复杂。
化成与老化
新制电池的第一次充放电循环称为“ 化成”。在形成过程中,由于寄生反应(例如产生初始SEI膜的反应)而损失了少量可循环锂。这种损耗减少了可用于充电循环的锂量。
在循环过程中,析锂也可能会与某一电极的基体紧密地结合,以至于正常的充放电循环不能再进行。同样,颗粒破裂会导致活性物质与电极的其余部分失去连接。这种现象将减少可循环材料的数量和电极容量。
通常,平衡电池时会补偿不可逆的可循环锂的损失量和形成过程中的主体容量。但是,即使可以保持良好的平衡,并通过在设备中实施循环电压约束来最大程度地减少老化寿命,也无法完全解决这些问题。随着电池的老化,可循环的锂和活性材料将不断丢失,从而导致动态的平衡问题。
电极平衡与建模
模型中准确的电极平衡的重要性不容质疑。如果热力学(即开路电势)不正确,则根本无法通过调节电导率,交换电流密度和扩散系数来补偿,这意味着电池开路电压永远不会准确,也无法平衡。
在下文中,我们将介绍用于电极平衡的数学框架,并在两个不同的示例中使用该框架。
电极平衡的数学框架
需要三个物理电荷参数来定义电池单元平衡:
- Q_\textrm{host,pos}(Ah) — 正极中的电量
- Q_\textrm{host,neg}(Ah) — 负极中的电量
- Q_\textrm{Li,tot}(Ah) — 两个电极中的总电量(可用于电化学反应)
对于每个电极,电极的锂化状态(SOL)定义为
和
其中,Q_\textrm{Li,pos}(Ah) 和 Q_\textrm{Li,neg}(Ah) 分别是存储在正极和负极中的锂原子的量。
现在,我们将介绍无量纲的参数Y。这些参数通过将相应的充电参数Q(Ah)除以电池的标准容量Q cell来实现无量纲:
为了定义电池的荷电状态(SOC),我们还需要将其中一个电极的锂化水平耦合到指定的SOC水平。
综上,需要四个参数来定义平衡模型:
- Y_\textrm{host,pos}— 正极中无量纲的电量
- Y_\textrm{host,neg}— 负极中无量纲的电量
- Y_\textrm{Li,tot}— 无量纲的锂总电量
- \textrm{SOL}_{\textrm{neg},0}— SOC为0%时负极的SOL
电极的SOL可以写成下式:
上述公式用于负极
上述公式用于正极。
当使用平衡表达式时,通常需注意,电极的无量纲电量直接与SOC和锂化程度有关,具体取决于
上述表达式表明,如果给定标称电池容量,可以实现(并允许)更宽的SOL循环窗口,并且可以通过减少电极中所需的活性材料量来增加电池的能量密度。
示例1:从电池工程师的角度选择电极平衡
我们有多种方式选择四个电极平衡参数。在此示例中,从电池工程师的角度来看问题,并基于以下命题构造一个平衡:
- 在SOC为0%时,选择负极中的最小锂化水平, \textrm{SOL}_\textrm{neg,0}(1)
- 在SOC为100%时,选择正极的最小锂化水平, \textrm{SOL}_\textrm{pos,100}(1)
- 负极中所需的相对过量主机容量, f_\textrm{excess}(1)
- 在形成过程中可循环锂的相对损耗, f_\textrm{loss}(1)
\textrm{SOL}_\textrm{neg,0} 可以直接在上面的框架中使用。
此处,多余容量定义为负极中存在的额外容量,相当于0%到100%SOC之间的循环过程中获得的容量;负极中存在的额外容量,相当于100%SOC时的锂化水平与完全锂化之间的余量。可以表示为:
f_\textrm{excess} \equiv \frac{1-\textrm{SOL}
_\textrm{neg,100}}{\textrm
{SOL}_\textrm{neg,100} – \textrm{SOL}_\textrm{neg,0}}
可以写作:
Y_\textrm{host,neg} = \frac{1+f_\textrm{excess}}{1-\textrm{SOL}_
\textrm{neg,0}}
确定Y_\textrm{host,pos}和 Y_\textrm{Li,tot} 比较棘手. 在形成过程中,首先假设所有可循环锂由于在负极中形成初始SEI层而损失,并且该容量损失与 Y_\textrm{host,neg}成正比。 因此,
f_\textrm{loss} \equiv \frac{Y_\textrm
{host,pos}
-Y_\textrm{Li,tot}}{Y_\textrm{host,neg}}
可以写作:
其次,我们使用SOC为100%的\textrm{SOL}_\textrm{pos} 和 \textrm{SOL}_\textrm{neg} 或更高 \textrm{SOL}_\textrm{pos,100} 时的公式来与其他参数相关:
\textrm{SOL}_\textrm{pos,100} = \frac{Y_\textrm{Li,tot}}{Y_\textrm{host,pos}} – \frac{\textrm
{SOL}_{\textrm{neg,100}}Y_\textrm{host,neg}}{Y_\textrm{host,pos}} = \frac{Y_\textrm{Li,tot}}{Y_\textrm{host,pos}} – \frac{\left(\textrm{SOL}
_{\textrm
{neg},0}Y_\textrm{host,neg}+1\right)}{Y_\textrm{host,pos}}
Y_\textrm{host,pos} 和 Y_\textrm{Li,tot}的表达式可重新排列为:
Y_\textrm{host,pos} = \frac{1+Y_\textrm{host,neg}(f_\textrm{loss}+\textrm{SOL}_{\textrm{neg}
,0})}{1-\textrm
{SOL}_\textrm{pos,100}}
Y_\textrm{Li,tot} = \frac{1+Y_\textrm{host,neg}(f_\textrm{loss}\textrm{SOL}_\textrm{pos,100}+\textrm{SOL}_{\textrm{neg},0})}{1-\textrm{SOL}
_\textrm{pos,100}}
示例2:使用COMSOL Multiphysics®对电极平衡进行反向设计
如引言和第一个示例所示,为了在模型中构建正确的电极平衡,需要大量的信息。如果任一参数有任何错误,则模型的开路电压可能会与实际电池的开路电压不同。商用电池(您尚未自己制造)的另一个问题是,可能根本不知道所需的参数。
在此示例中,我们将从电池的实验性开路电压和一些基本假设出发,使用反向设计方法作为电极平衡的替代方法,然后通过优化求解器找到合适的电极平衡。
电池的实验开路电压如下图所示。在这种情况下,当开路电压由3.0 V变为4.15 V时,电池SOC由0变为1。
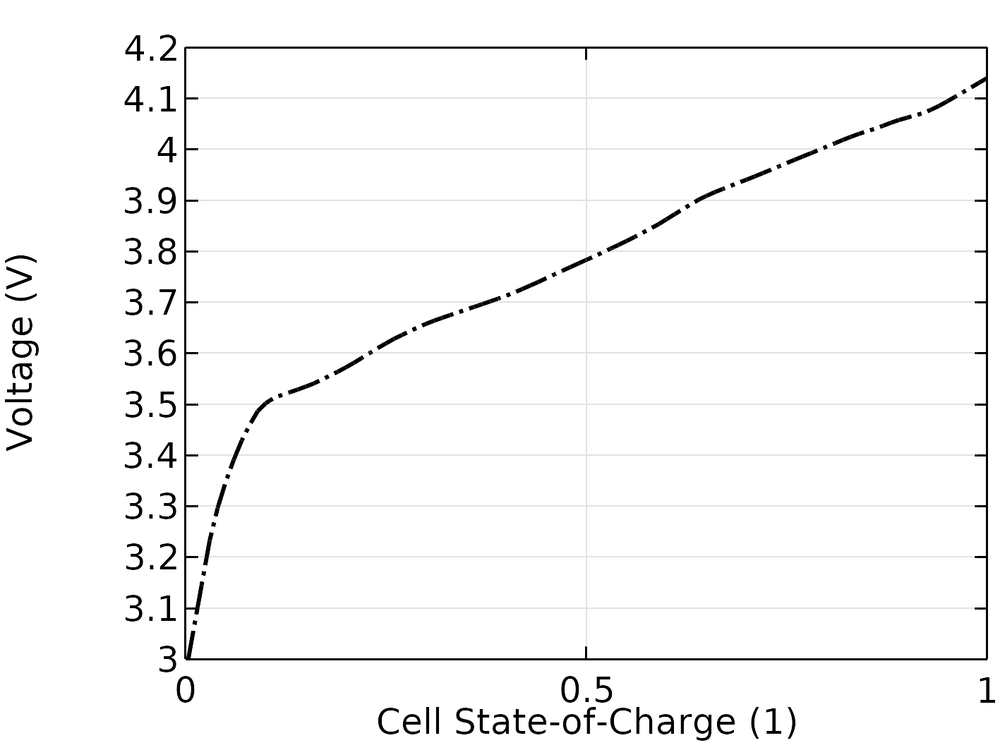
实测开路电压与电池SOC的关系。
假定该电池为(1:1:1)LiNiMnCo(NMC)-石墨电池。为了构建电池开路电势,我们使用了电池和燃料电池模块(COMSOL Multiphysics的一个附加模块)材料库中电极材料的平衡电位曲线。这些曲线基于实验的半电池数据,并表示为平衡电位E eq(V)的插值函数,它是锂化状态(SOL)的函数,如下所示。
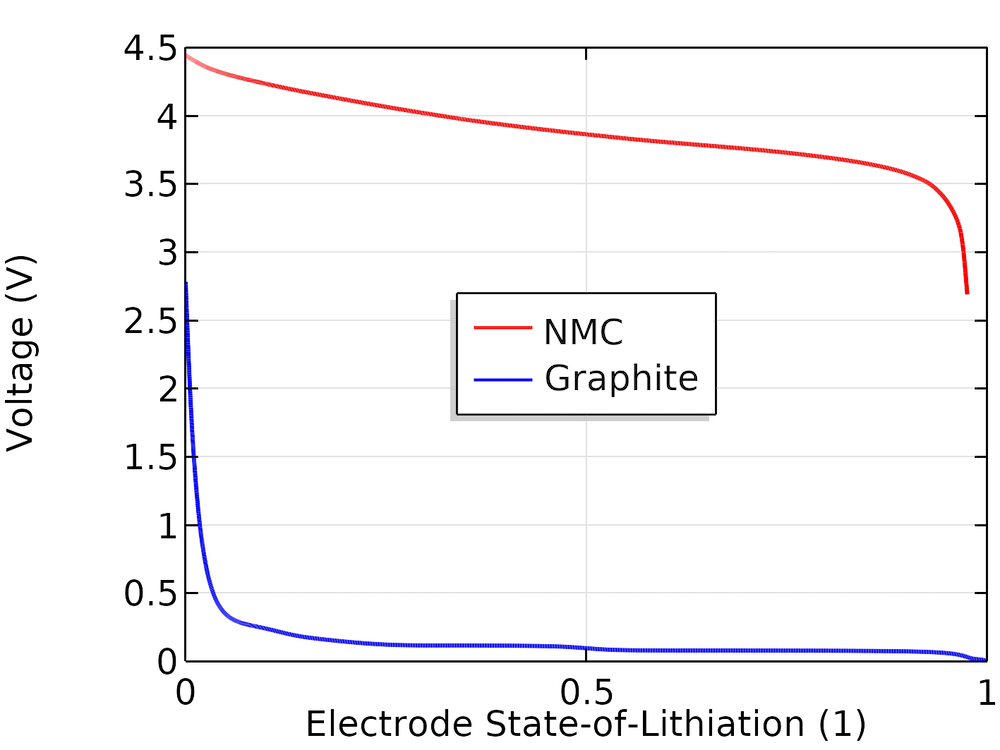
平衡电极电位与SOL的关系
使用上面的数学框架,将电池开路电势构造为正负开路电压之差:
在使用优化解算器的过程中,利用COMSOL Multiphysics软件执行四个拟合参数的参数估计 (Y_\textrm{host,pos}, Y_\textrm{host,neg},Y_\textrm{Li,tot},和 \textrm{SOL}_{\textrm{neg},0})
对于实验开路电位(OCP)曲线与SOC的所有数据点,使用最小二乘方法和最小化目标函数,将ø 定义为:
结果与讨论
实验和建模的电池电压与电池SOC的关系以及各个电极的电压值如下所示。可以看到,对于该特定电池,半电池曲线与真实的实验电池OCP吻合。
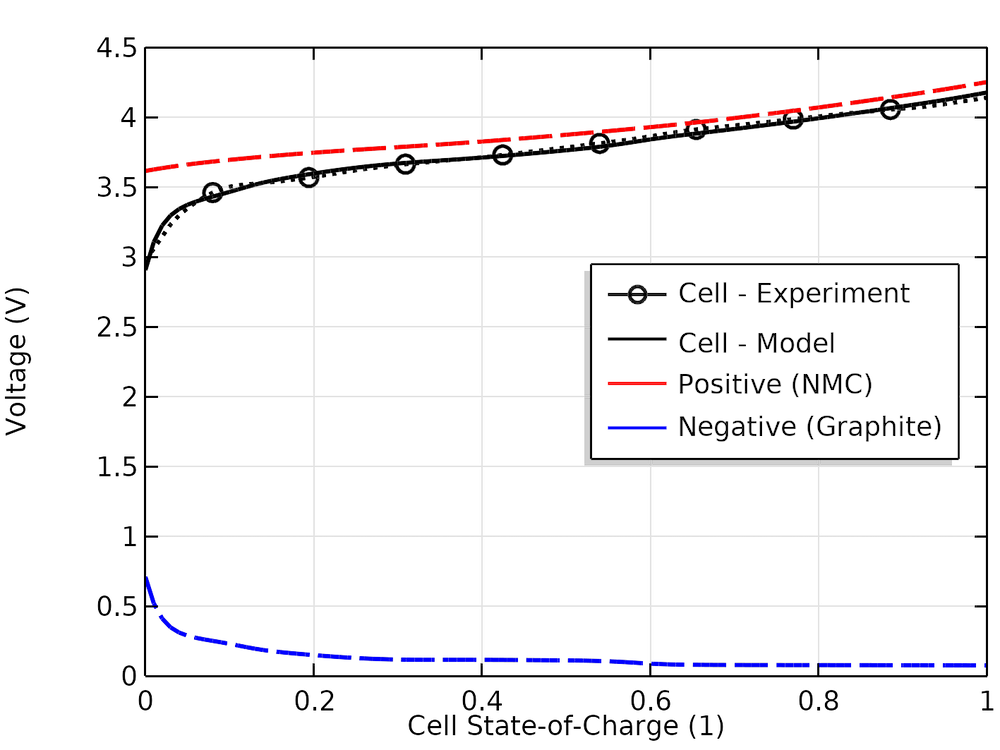
电池开路电压的实测值、模拟值与SOC的关系,以及相关的正负电极电压。
下表为拟合的参数值。术语Y_\textrm{Li,tot} 高于1,表示在单元OCP曲线的电压窗口内循环时未使用所有容量。类似地,Y_\textrm{host,neg} 高于1,表示在负极大约有25%的剩余容量,以便在充电过程中相对于析锂具有潜在的余量。(参见示例1中 f_\textrm{excess} 的定义)我们还注意到, Y_\textrm{Li, tot}比Y_\textrm{host,pos}小10%, 得到锂形成过程中损失的量的量度 (参见 定义1中f_\textrm{loss} 的示例).
| 参数 | 拟合值 |
|---|---|
| Y_\textrm{host,pos} | 1.27 |
| Y_\textrm{host,neg} | 1.22 |
| Y_\textrm{Li, tot} | 1.14 |
| \textrm{SOL}_{\textrm{neg},0} | 0.025 |
下图显示了电池电压和相应的SOL值随电池SOC的变化,表示在拟合模型中,当电极在0%至100%电池SOC之间循环时,电极的实际SOL循环窗口。
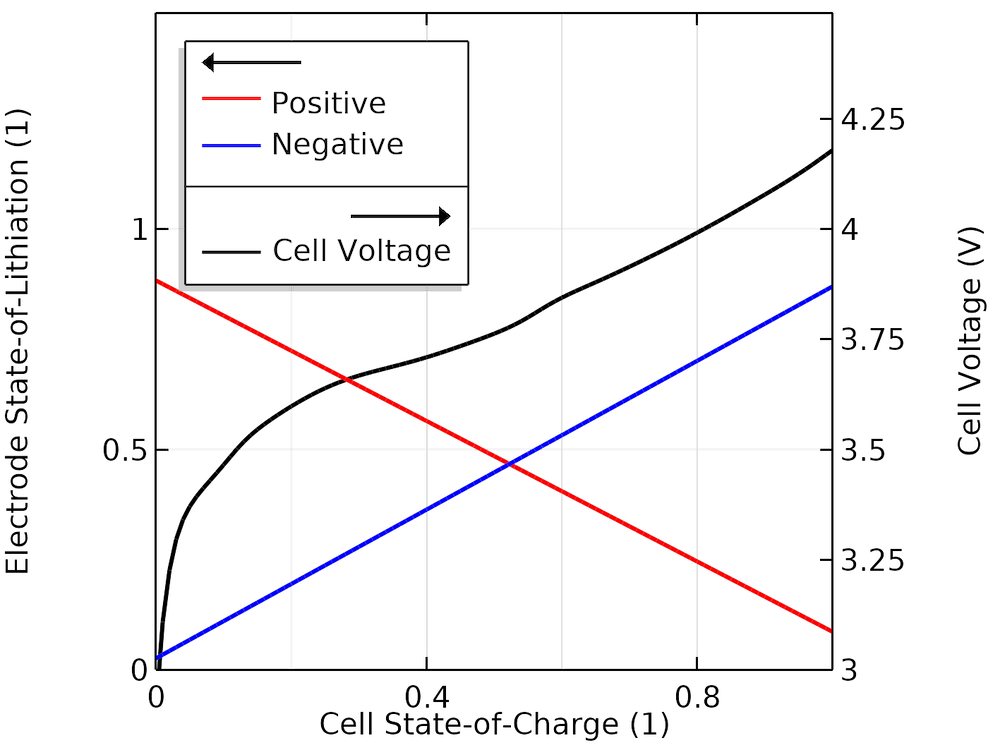
每个电极中拟合的SOL与SOC的关系。
毫无疑问,上述拟合方法可用于模型中并获得适当的电极平衡。但是,它也可以直接分析电池的老化(健康状态)。假设半电池平衡电势曲线相对于SOL的形状对于老化电池没有变化,我们可以随时执行上述拟合过程以监控电池的健康状态。拟合值的变化Y_\textrm{Li, tot}, Y_\textrm{host,neg}, 或 Y_\textrm{host,pos},则对应于可循环的锂和/或基质材料的损失。我们可以将其视为常用dVdQ方法的补充方法,在该方法中,将分析开路电压与SOC曲线导数中的峰值位置。
使用电池平衡参数进行高级建模
现在可以使用四个电极平衡参数中的任何一组来构建更高级的模型。例如,用于预测不同速率下的充放电容量的性能建模,或某些与电位相关的老化反应的详细建模。
例如,上面的参数将对应于COMSOL Multiphysics中锂离子电池界面中的下列表达式
和
其中,积分分别取自正极和负极域。在此,\varepsilon_s 是电极的孔隙率,c_{s,\textrm{max}} (mol/m3) 是嵌入的锂的最大浓度。即电极相的体积主体理论容量。
假设每个电极中的电极特性都是恒定的,则可以按如下方式设置电极体积分数:
\varepsilon_{s,\textrm{neg}} = \frac{Y_\textrm
{host, neg}
Q_\textrm{cell}} {F c_{s,\textrm{max,neg}} L_\textrm{neg} A}
和
\varepsilon_{s,\textrm{pos}} = \frac{Y_\textrm
{host, pos}
Q_\textrm{cell}} {F c_{s,\textrm{max,pos}} L_\textrm{pos} A}
其中, L_\textrm{neg}(m) 和 L_\textrm{pos} 是每个电极的厚度,A (m2) 是电极平面的面积。
其余两个参数与电极中嵌入的锂浓度的初始值有关。在多孔电极模型中,锂化的局部状态定义为:
\textrm{SOL} \equiv \frac{c_s}{c_{s, \textrm
{max}}}
其中, c_s为嵌入锂的局部浓度。
因此,初始浓度的表达式可以从上述SOL neg和SOL pos的表达式中得出。例如,将初始浓度设置为与上述的0%电池对应的SOC。
c_{s,\textrm{init},\textrm{neg}} = c_{s,\textrm{max}
,\textrm{neg}} \textrm{SOL}_{\textrm
{neg},0}
在负极域;
c_{s, \textrm{init},\textrm{pos}} = c_{s,\textrm{max},\textrm{pos}}\left(\frac{Y_\textrm{Li, tot}}{Y_\textrm{host,pos}} – \frac{\textrm{SOL}_{\textrm{neg}
,0}Y_\textrm{host,neg}}{Y_\textrm{host,pos}}\right)
在正极域。
下一步
要了解“电池与燃料电池”模块中电池建模的特性和功能,请单击以下按钮:
扩展阅读
在这些博客文章中了解有关锂离子电池建模的更多信息:






评论 (6)
剑波 叶
2021-11-15示例一倒数第2个表达式,Yhost_pos中公式右侧的分子括号部分,应该是相加,而不是相乘,“floss+SOLneg,0”。
hao huang
2021-11-17 COMSOL 员工感谢指正,中英文页面均已修改。
俊 张
2023-01-08能否解释一下SOLneg和SOLpos表达式的推导过程呢
翀 施
2023-01-17 COMSOL 员工张俊你好,推导过程其实就是按照SOLneg和SOLpos的恒等式以及Yi来推导的,比如SOLneg=QLi,neg/Qhost,pos=(QLi,neg/Qcell)/(Qhost,neg/Qcell)=SOC/Yhost,neg,因为SOC是根据负极的嵌锂量计算的,所以SOC=QLi,neg/Qcell成立,Yhost,neg则根据Yi的定义。按照同样的思路也可得SOLpos。
森 于
2024-04-11请问因变量中的内部变量comp1.liion.Q_cell_init是如何计算的,如何查看comsol中它使用的公式
yongchao wang
2024-04-19 COMSOL 员工可以通过“SOC 和初始电荷分布 1”节点中的“方程”理解变量comp1.liion.Q_cell_init的计算过程,也可以通过帮助文档查看该变量的详细计算公式,参考连接内“CELL CAPACITY AND STATE OF CHARGE”部分的说明:https://doc.comsol.com/6.2/docserver/#!/com.comsol.help.battery/battery_ug_electrochem_battery.06.56.html%23772830