
今天,来自 Acculution ApS 的特邀博主 René Christensen 将与我们一起探讨 COMSOL Multiphysics® 软件 6.2 版本中新增的 部分分式拟合 功能。
COMSOL Multiphysics® 6.2 版本软件新增的 部分分式拟合 功能通过分析频率复数函数的实部和虚部,得出几个分式的总和来拟合该函数,并在相关频率范围内以一种非常严谨的方式描述系统。这些分式被称为部分分式,它们共同构成一个数值传递函数,不仅可以帮助深入理解的底层的运行机理,还能轻松变换到时域。输入值的实部和虚部通常来自 之前的 模拟,也可以来自其他软件甚至测量值。
内容简介
时频变换
由于该功能涉及频域分析,因此简要介绍一下在频域工作的相关功能以及如何实现信号和系统的频域分析是很有意义的。
虽然信号通常会随时间变化,但是在频域对其进行分析往往更为简单。同样,对系统进行分析时,最常用的方法是将其时域特征的某些方面变换到频域。时域和频域之间的变换通常通过傅里叶变换或拉普拉斯变换以及各自的逆变换来完成,这两种变换有很多重复,这里我们将重点讨论拉普拉斯变换,因为它适用于系统分析的经典变换。已知拉普拉斯变换的单边积分形式:
式中, s 是通过角频率 \omega 和阻尼 \sigma 定义的复频率,即
这种单边性使该积分适用于系统分析,因为系统可以有一个特定的“开启”时间,并且可以研究瞬态行为。此外,拉普拉斯变换将作为建立即将讨论的传递函数的主要变换。下表列出了一些重要的时域与频域的对应关系。
| f(t) | F(s) |
|---|---|
| kf^{(n)}(t) | s k F(s) + k f(0) |
| k \int^{t}_0 f(\tau) d\tau | k\frac{F(s)}{s} |
| t^n e^{-\sigma_0 t} | \frac{n!}{(s+\sigma_0)^{n+1}} |
| ke^{-\sigma_0t}\cos(\omega_0t) | k \frac{s + \sigma_0}{(s + \sigma_0)^2 + \omega^2_0} |
| ke^{-\sigma_0t}\sin(\omega_0t) | k \frac{\omega_0}{(s+\sigma_0)^2 + \omega^2_0} |
传递函数
许多系统可以通过包含常数和实数系数的线性微分方程来描述,形成实数和线性时不变(LTI)系统。例如,外力(输入)为 f_\textrm{ext},速度(输出)为 v 的质量-弹簧-阻尼系统:
式中,m 是质量,r 是阻力,k 是刚度。这里,我们用速度而不是位移或加速度来表示方程,因为力和速度是功率共轭变量,就像电力系统中的电压和电流一样。
然后,在稳态假设下进行拉普拉斯变换,即假设使用复指数形式表示输入F(s) = (F_0e^{\phi_F(s)})e^{st} 和输出 V(s) = (V_0e^{\phi_V(s)})e^{st} 的振荡和可能存在的阻尼,其中, F_0 和 V_0 为实数。根据此假设,就可以对系统进行频域描述:
此处忽略了初始条件,但也可将其纳入上述方程。由于我们关注的是输入 X(s) 后的输出 Y(s) 结果,因此可以使用一般的传递函数:
对于当前的系统,得到以下传递函数:
在工程动力学中,与线性时不变系统相关的传递函数通常是有理函数,一种只包含变量 s 的两个单变量多项式的分数:
也可以用分式形式的零点和极点表示:
其中
有理传递函数的一个显著特点是它们的阶数,也就是此处分母中的 s 最高阶数,它可由指数 n 直接获得。另一个特点是它的正当性。有三种类型需要考虑。一类称为真分式,即分母的阶数大于或等于分子的阶数,n \geq m 。另一类是子集,称为严格真分式,其极点数(严格地)高于零点数,即 n > m。第三类是假分式,即 n < m。对于最后一种情况,应考虑潜在的稳定性和因果性问题,但真分式还会受到是对特定传递函数还是其逆函数进行分析的影响。
对于质量–弹簧–阻尼系统而言,传递函数属于带通滤波器的范畴,这是合理的,因为在特定频率下,施加的力会在速度上产生共振。带通滤波器函数的标准形式为
由此得到特征角频率为:
和
质量-弹簧-阻尼系统的阶数为 2。这也意味着分母多项式有两个相关联的根:极点。对于本文考虑的实值系统,这两个极点有三种可能:1)两个不同的实极点;2)两个重叠(重复)的实极点;或 3)两个共轭复极点。分子的根称为零点,在收敛区域(ROC)已知的情况下,零点和极点将完全可以描述相关的线性时不变实系数系统。在此,我们假设系统是因果性,因此可以通过该信息获知收敛区域。这将导致稳定系统在复平面 s 的右半平面没有极点,同时确保存在傅里叶变换,这正是从传递函数中找到频率响应的必要条件。由于系统为实值且存在共轭对称性,因此如前所述,复极点总是成对出现。
部分分式分解
在学习传递函数和(逆)傅里叶/拉普拉斯变换时,可能会遇到部分分式分解的主题(这样做通常是为了通过表格更容易地找到逆拉普拉斯变换)。高阶传递函数可以分解成更简单的分式,由于相关系统的线性关系成立,它们的逆变换加起来就是总逆变换。当求解包含有理函数的积分时,也可能与此相关。最后,在控制理论中将高阶传递函数分解为多个低阶分式也很有意义。
现在,我们来说明将传递函数分解为部分分式的过程,其中的极点可以写成因式分解的形式。传递函数的阶数为 5,双重复极点为-5,三重复极点为 0,因此我们需要 5 个部分分式:
等式两边同乘分母,得到
对比左右两边的不同阶数,得到未知数分别为 A=0.52, B = -1.6, C=4, D=-0.52, E=-1。
利用逆拉普拉斯变换表格,我们可以求出相关系统的脉冲响应为:
直接对原始传递函数进行逆变换需要使用数学软件,但通过部分分式分解,至少在零点和极点数值已知的情况下,可以手动分析完成。请注意,对于假分式传递函数,可能需要进行多项式长除法,才能将原始传递函数拆分为渐近值和后续分式。
通过 部分分式拟合(PFF)功能,我们可以充分利用时间与频率的关系,在瞬态声学中使用随频率变化的阻抗。
部分分式拟合
虽然我们通常无法为模拟的多物理场问题找到解析的传递函数,但可以找到输出与输入之间的比值,并将其作为表格中的复值。这些比值可以是模拟的输出,也可以是导入的测量值。现在,如果有办法由表格中的数值建立传递函数,就能深入理解系统,而直接从数值本身是很难理解的。还可以解析逆傅里叶变换来形成脉冲响应,不必进行如逆快速傅里叶变换等研究。最后,用零点和极点而不是大量的表格数据来描述系统,可以在保留系统的所有特性的同时使系统更加准确,至少在所选的表格值频率范围内是这样。这基本上就是 COMSOL Multiphysics® 中 部分分式拟合 功能可以实现的,即通过频率与复值的函数关系建立数值传递函数。
在部分分式拟合函数节点中,输入的数值来自表格,其中包含实数、虚数和频率。部分分式拟合将对这些值进行拟合,得到描述底层系统的传递函数的部分分式形式。部分分式拟合基于”改进的自适应 Antoulas–Anderson (AAA) 算法,AAA2 ”(见 COMSOL Multiphysics Reference Manual),其数学形式为:
方程的第一项是与拟合系统的适应性相关的渐近值,我们可以通过示例来了解它是如何起作用的。第一个求和项是对拟合函数找到的所有实值极点求和,残差也是实值。第二个求和项是对拟合过程找到的复值极点求和,残差也是复值。可以看到,复值极点和残差预计会以复值共轭对的形式出现,其中一个复值极点是另一个的镜像。稍后我们将讨论部分分式拟合结果的共轭对称性假设如何不影响到输入数值的底层系统,因此这些系统是真实或在物理上是否可实现并没有限制。
还应注意的是,在上述表达式中,x 是频率,而不是详细说明传递函数基本原理时使用的角频率 \omega 。此外,所有分式都是一阶的,且分子中包含常数,因此对于重复的极点,可能需要做一些工作将其重新表述为部分分式分解方法所示的形式,一般来说,分子中可能有更高的阶数。除此之外,部分分式拟合本质上是以部分分式的形式得到数值传递函数,因此掌握基本的信号处理知识非常有用,包括接下来我们使用不同的示例来探究其功能的时候。
实极点
为了解如何利用这一功能找到实极点,我们将部分分式拟合应用于已知的简单解析传递函数,来了解其运行方式和得到的结果。首先,测试部分分式拟合功能输出的一阶低通滤波器函数:
这里,p = -1 有一个实极点,当因子(或系数)K_\textrm{DC} 被合并到分子中时,实数残差为 5。现在,我们来看看部分分式拟合函数能否求解。已知传递函数,我们就能计算出其频率响应的实值和虚值。接下来,将这些值输入部分分式拟合。我们可以将表格值(方形标记)与拟合值(实线)绘制在一起,看看拟合效果如何。在这种情况下,拟合效果看似完美,我们不仅要看曲线,还要研究实际输出,这才有意义。
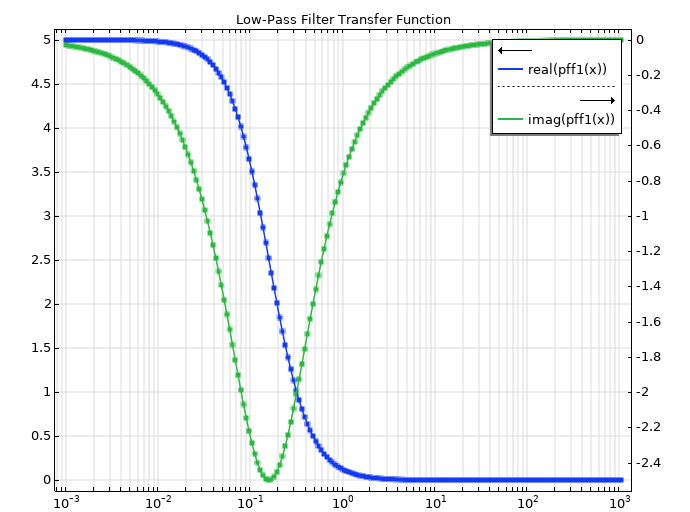
显示的部分分式拟合结果为拟合的残差和极值:
| 参数 | 值 | 按2\pi的比例缩放后的值 |
|---|---|---|
| Y_\infty | 6.547\cdot 10^{-15}+3.78\cdot 10^{-16}i | N/A |
| R_1 | 0.796 | 5 |
| \xi_1 | -0.159 | -1 |
渐近值基本为零,这正是此类有理函数的预期值。由于部分分式拟合中的 x 是以赫兹为单位的频率,而不是以弧度/秒为单位的角频率,因此计算的极点也是正确的,这样传递函数中的极点就比通过部分分式拟合计算的极点高 2\pi。由于这一缩放贯穿整个方程,因此 0.796 的残差比预期的 5 \cdot 1 低约 2\pi,因此所有值都与真分式的缩放值一致。
对另一个实极点进行研究后,其传递函数如下:
由上述传递函数可以直接看到极点,因此可以手动计算部分分式,得到
预计在频率缩放范围内,极点 \text{p}=-1 得到的残差为 1,极点 \text{p}=-2 会得的到残差为 -1。这就是我们得到的基本结果:
| 参数 | 值 | 按 2\pi 比例缩放后的值 |
|---|---|---|
| Y_\infty | 7.151 \cdot 10^{-12} – 1.513 \cdot 10^{-11} i | N/A |
| R_1 | -0.159 | -1 |
| \xi_1 | -0.318 | -1.998 |
| R_2 | 0.159 | 1 |
| \xi_2 | -0.159 | -1 |
渐近项基本为零,如果将极点和残差乘以 2\pi ,并翻转它们的阶数,就能得到预期值。因此,多重实极点得到了正确处理。
复极点
另一个更接近物理系统的例子是挡板中集总扬声器驱动器的压力输出,其简单的集总电路如下图所示:
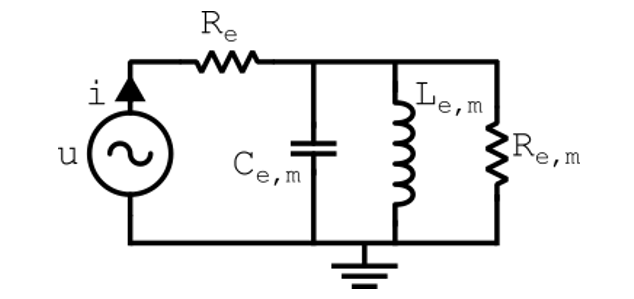
压力输出将与二阶传递函数成比例关系,可表示为
与
和
声压级如下图所示,既包含作为集总模型灵感的底层模拟驱动器,也包含下表中的集总参数。
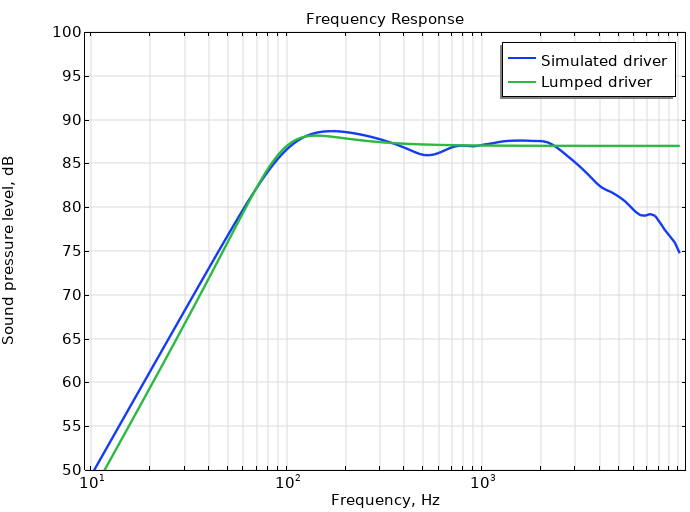
| 集总参数 | 值 | 单位 |
|---|---|---|
| Bl | 5 | T \cdot m |
| R_e | 6 | \Omega |
| M_m | 13 | g |
| K_m | 5 | N/mm |
| R_m | 4 | N\cdot s/m |
| L_{e,m}= Bl^2/K_m | 5 | mH |
| C_{e,m}= M_m/Bl^2 | 520 | \mu F |
| R_{e,m}= Bl^2 /R_m | 6.25 | \Omega |
| \omega_0 | 620 | 1/s |
| Q_t | 0.98722 | 1 |
对于给定的 Q 值,我们可以确保角频率的复极点约为 s_{1,2} = -314 \pm 534 i,或常规频率的复极点约为 x_{1,2} = -50 \pm 85 i 。将传递函数中的 K 值设置为 1,对函数进行简单缩放,然后运行集总模型分析。输入传递函数值的部分分式拟合,得到以下值:
| 参数 | 值 |
|---|---|
| Y_\infty | 1+2.85\cdot 10^{-15} i |
| R_1 | -5.697\cdot 10^{-13} |
| \xi_1 | 99.992 |
| Q_1, Q^\ast_1 | -99.982 \pm 55.744 i |
| \zeta_1, \zeta^\ast_1 | -49.991 \pm 85.108 i |
渐近项基本上等于 1,这是这个适当但并非严格适当的传递函数的预期值。有一个实极点和两个复极点。从图中可以看出,实极点不稳定,但残差很小,可以直接删除。其余复极点的值与传递函数一致,因此,您可以利用部分分式拟合的结果得到瞬态响应,也可以在底层驱动模拟数据上运行部分分式拟合,而不是在近似集总模型上运行。在这种情况下,会找到更多的极点,但方法与集总模型相同。
重复极点
传递函数可能有重复极点,比如多个极点位于 s 平面的同一位置。正如本文部分分式分解部分所述,在对这种情况解析部分分式分解时,通常会将总和拆分为一些分母阶次大于 1 的分式,而部分分式拟合只得到一阶分式。部分分式分解法得到的值仍然是正确的,但已确定对所发现的值具有高度敏感性,因此,如果要将计算出的极值或残差导出并在其他软件中使用,则不应截断这些极值或残差。
不稳定极点
在进行部分分式拟合时,可能会发现不稳定的极点。在这种情况下,应该首先查看这些极点的残差,并与稳定极点的残差进行比较。残差可忽略不计的不稳定极点可以去除,不会影响整体拟合。如果不稳定极点对拟合精度有重大影响,则应考虑正在研究的底层系统的类型。如果系统是无源的,那么它本身就是稳定的,因此了解信号处理基础知识有助于确定在相关频率范围内表现出不稳定行为的模拟或测量问题。部分分式拟合函数提供了一个名为 翻转极点 的选项,可以将不稳定极点镜像到 s 平面上的稳定位置。这可能会影响拟合精度,但可以通过重新绘制新的拟合图来立即评估其效果。不稳定极点通常位于低频附近,因此翻转不稳定极点可能只会对低频产生轻微影响,但高频特性不变。
一般来说,翻转不稳定极点会影响相位响应,同时保留幅值响应,但请记住,要正确解释稳定性,必须考虑因果关系假设。此外,如果大部分或所有极点都不稳定,则可能表明拟合的数据对应于一个稳定函数的逆函数,因此最好评估逆函数。
需要注意的是,应针对更多的传递函数进行有关不稳定极点和(或)重复极点的观测,以更好地掌握其功能,因此上述分析不应被视为概括了所有情况,而仅仅是作为介绍其功能的一些情况。此外,研究系统无源性的正式定义(参考文献 1 和参考文献 2)也是有意义的,本文无需进一步探讨相关条件,只需说明通常可以通过评估拟合数据中的所有实值是否为正值来进行无源性检查。
非有理传递函数:时间延迟
并非所有物理现象都能通过有理传递函数轻松描述,因此我们来看看部分分式拟合对非有理传递函数的拟合效果如何。第一个例子是 T 秒的时间延迟,代表一个重要的传递函数,但并不是传统的有理传递函数:
传递函数是在时间延迟为 1 秒的特定频率范围内计算得出的,对于该频率范围和特定的设定容差,部分分式拟合得到的渐近项约为负 1 且只有一个实极点。
| 参数 | 值 |
|---|---|
| Y_\infty | -1+3.405 \cdot 10^{-16} i |
| R_1 | 0.6155 |
| \xi_1 | -0.3078 |
曲线看起来拟合地非常好:
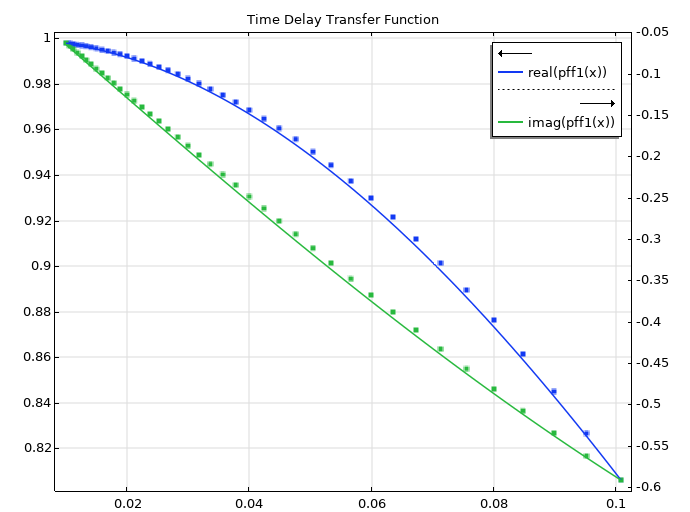
不过,我们还可以更进一步建立传递函数。根据渐近值,可以知道传递函数的类型是真分式。我们可以合并项并计算出精确的传递函数:
通过观察数值,我们发现残差值为极值的两倍。因此,上述表达式可以改写为
我们现在看到的是一个一阶的全通滤波器,这是合理的,因为延时器的幅值响应必须是平坦的。但还可以更进一步计算。如果分子和分母的阶数都是 1,只需找到 H(s) = e^{-sT} 的帕德近似 P_{1,1}(s)(相当于双线性变换),即可得到结果:
这非常接近部分分式拟合的结果。事实上,当把上述表达式转换成 ix 格式时,T=1 ,就可以得到:
令1/\pi = 0.3183 ,可以看到结果与部分分式拟合得出的结果只有很小的百分比差异。如果频率范围更大,则需要更多的极点,而且很可能会发现找到的极点代表贝塞尔多项式的根(参考文献 4)。
非有理传递函数:微声学
另一个非有理测试传递函数是关于微声学的示例。考虑一个横截面如下图所示的矩形狭缝(参考文献 5):
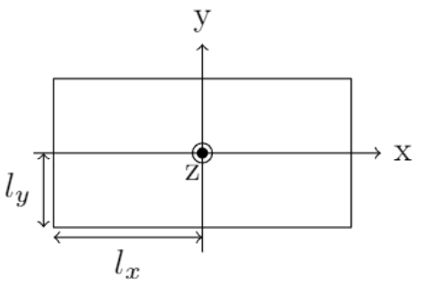
该横截面管道将在每单位长度 Z^\prime 内具有相关的声串联阻抗,以及每单位长度 Y^\prime 的声学并联导纳。这些都不能直接写成有理函数形式,但可以通过较低频率下的有源和无源元件近似,并且使用部分分式拟合能达到什么效果将非常有趣。
我们假设狭缝非常细:l_y \ll l_x 。这种狭缝在每单位长度内的串联阻抗如下(参考文献 5):
这里,S = 4l_x l_y 是狭缝的面积;\rho_0 是空气的密度;x_v = i \omega l^2_y/v ,其中 v = \mu_0 / \rho_0 和 \mu_0 是空气的黏度。将该表达式简化的一种方法是应用泰勒展开,得出如下的集总模型(参考文献 5):
低频下的串联阻抗可分为有源恒阻部分和无源恒质部分。这可以看作是一个假传递函数,但它只适用于较低的频率。因此,让我们来看看部分分式拟合能得到什么结果。我们建立了一个二维模拟,可以计算并得到特定频率范围内的阻抗,同时考虑声学和微声学效应,来揭示底层系统的特征。还必须为几何参数选择一些数值。这里,将l_x 设置为 1 cm, l_y 设置为 0.5 mm。我们可以清楚地看到,在所选几何尺寸下,黏性边界层随频率变化,在整个音频范围内厚度有大有小。

现在,我们将计算出的串联阻抗输入部分分式拟合功能。由于解析表达式中没有明确的零点或极点,无法立即猜测部分分式拟合的结果。拟合过程能很好地为残差和极点找到合适的参数,从而实现串联阻抗的拟合曲线,而且可以看到实部是如何随着频率的降低而保持不变的(泊肃叶流),这在集总模型中已经可以观察到。
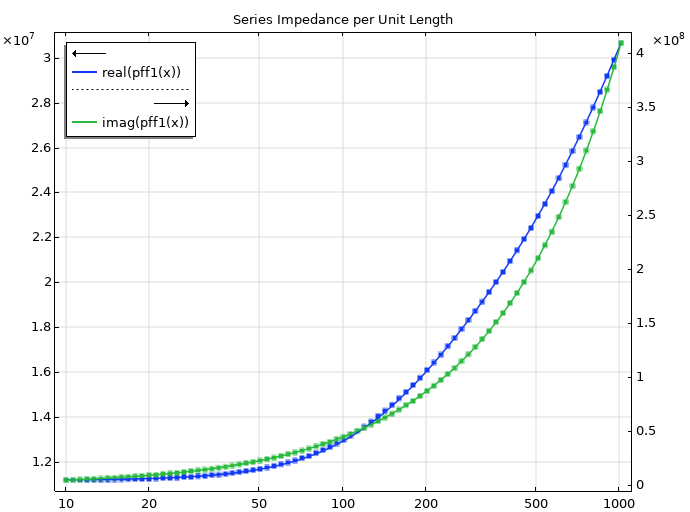
部分分式拟合得到的有限渐近值和三个实极点如下表所示:
| 参数 | 值 |
|---|---|
| Y_\infty | 9.336 \cdot 10^{10} + 0.135i |
| R_1 | -1.631\cdot 10^{10} |
| R_3 | -1.901 \cdot 10^9 |
| \xi_1 | -237665.182 |
| \xi_2 | -935.471 |
| \xi_3 | -217.677 |
得知部分分式拟合在选定的频率范围内拟合时找到的极点数,就可以尝试理解这个结果了。虽然串联阻抗不是通过有理函数而是通过三角函数来描述的,仍然可以通过帕德近似值对其进行近似。由于部分分式拟合中有一个非零渐近项和三个极点,因此 P_{3,3} 近似值是我们需要寻找的:
式中, a = \rho_0/S , b = l^2_y/v。计算一下,基本上就能得到部分分式拟合获得的结果。
虽然由于几何结构较简单,我们可以事先通过解析方法得到单位长度的串联阻抗,但能够使用解析方法来拟合传递函数,还是非常有参考价值的。当然,我们这里的实际示例是拟合给定模拟的数值结果,而没有使用任何基本数学表达式解析。
这里选择的频率相对较低,因此研究更高频率下的拟合效果是有意义的。通过观察精确阻抗在较高频率下的表现,我们可以发现底层传递函数不是真分式。由于部分分式拟合功能在设计上会得到一个真分式的拟合传递函数,因此我们应该看到在输入频率以外的更高频率下,精确阻抗与拟合值之间会出现偏差,这就是下图所示的情况。任何拟合都只会考虑到部分分式拟合提供的频率范围,而不会保证在此范围之外的拟合效果。这也与帕德近似的渐近行为有关,但我们在此不再赘述。最后,需要指出的是,您可以研究任何相关系统的逆系统,这将改变有理传递函数的真假性,但即便如此,在拟合过程中使用的频率范围之外的值仍会出现偏差。
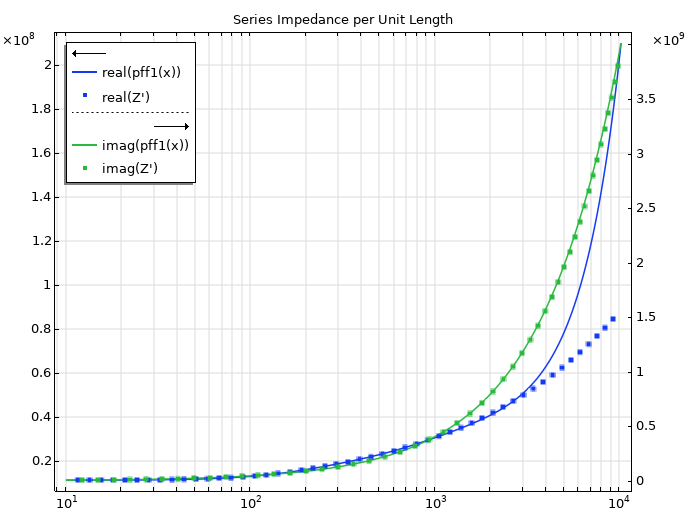
最后,可以根据部分分式拟合结果合成一个电路,如下图所示。电路计算将接近小狭缝长度 dL 的串联阻抗,其精度与相同频率范围内的部分分式拟合极值和残差相同。本篇博客不涉及合成的细节,但应该指出的是,还应以类似方式建立并联导纳来完整描述狭缝。
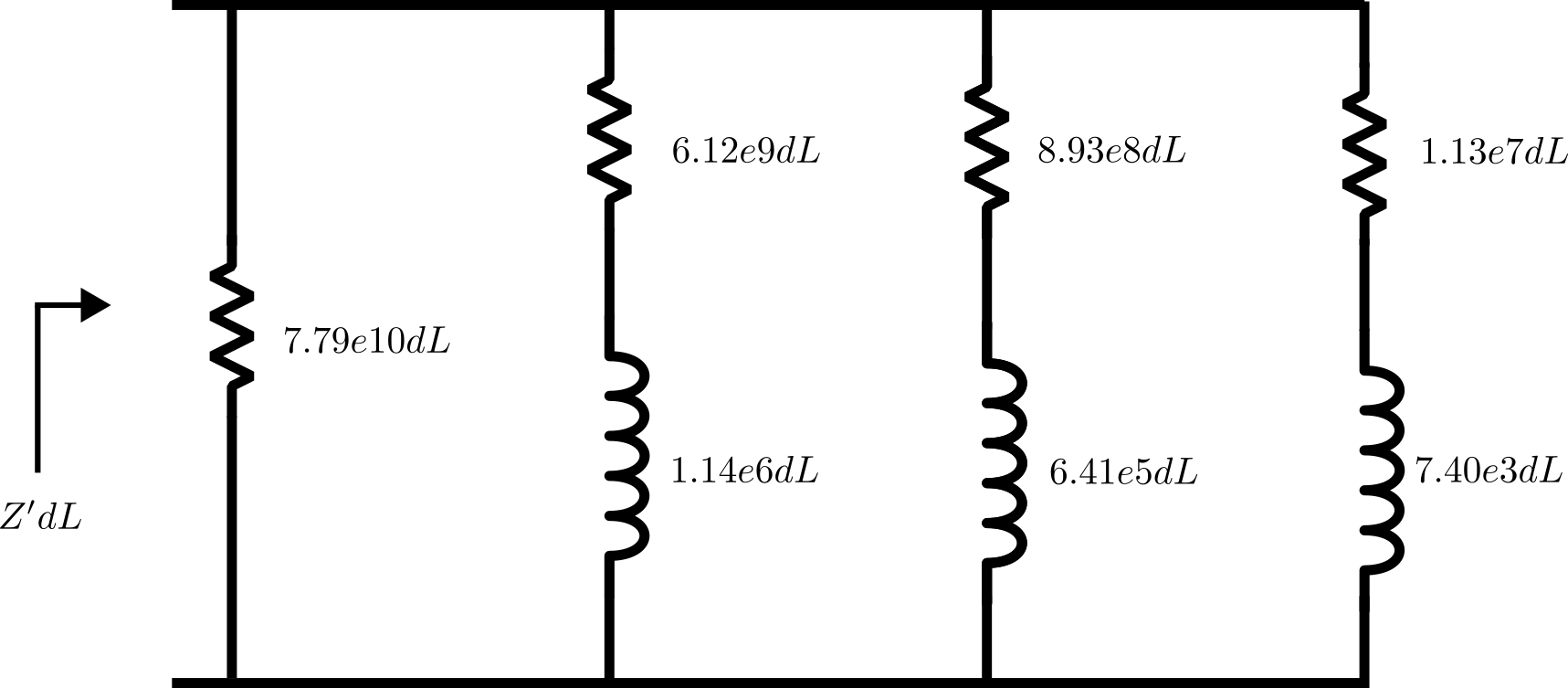
共轭对称,负频率
如前所述,部分分式拟合中的复极点将以复共轭对的形式出现。然而,原始系统必须为实数并不是一个明确的约束条件,因此它可能具有固有的共轭对称性,也可能没有。由于部分分式拟合本身具有共轭对称性假设,我们必须将输入值的频率范围限制为正频率(可能包括 0 Hz)或负频率(可能包括 0 Hz)。前者可能比后者更常见,但两种选择都有。由于初始数据可能不存在共轭对称性,因此这两个选项可能无法得到相同的拟合近似值。
结束语
本文介绍了 COMSOL Multiphysics® 中新增的 部分分式拟合 功能在不同情况下的表现,如严格真分式、真分式和假分式的有理传递函数,以及非有理系统特性,如时间延迟、微声学效应或耦合多物理场仿真结果。该功能性能优异,可通过更改频率范围和容差选项以及直接更改残差和极点值进行手动拟合。
值得注意的是,对于某些具有实极点(在无限频率范围内)的测试传递函数,部分分式拟合有时会在其有限频率范围内得到复极点。不过,与实部相比,虚部非常小,因此很容易就能得知这在数值上仍然是合理的。请注意一种情况,即只包含实部就可以进一步简化。有时您还会看到极小的残差,因此相关极点可能并不重要,可以从部分分式拟合中删除。您还可以添加或删除极点和残差,并查看对拟合曲线的影响,这是一项非常有用的功能。
我对最新版本中的这个功能非常满意,并且这个功能可用于很多相关的应用案例。
动手尝试
想自己动手尝试 部分分式拟合 功能吗?请查看 COMSOL 案例库中的管道与耦合器测量装置的输入阻抗:使用部分分式拟合的时域模型降阶 (MOR)模型。
参考文献
- B. D. O. Anderson and S. Vongpanitlerd, Network Analysis and Synthesis, New Jersey: Prentice-Hall, Inc., 1973.
- Y. Miki, “Acoustical properties of porous material – Modifications of Delany-Bazley models -”, The Journal of the Acoustical Society Japan, vol. 11, no. 1, pp. 19–24, 1990.
- A. V. Oppenheim and R. W. Schafer, Discrete-Time Signal Processing, New Jersey: Prentice Hall, Inc., 1989.
- J. R. Martinez, “Transfer Functions of Generalized Bessel Polynomials”, IEEE Transactions On Circuits And Systems, vol. CAS-24, no. 6, 1977.
- M. R. Stinson, “The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape”, J. Acoust. Soc. Am. 89 (2), 1991.



评论 (2)
刘乐
2024-11-25部分分式分解利用逆拉普拉斯分解貌似漏了exp,知道D=-0.52下应为-0.52*exp(-5t)而非文中的-0.52^(-5t)
Yuqing Ge
2024-12-05 COMSOL 员工的确,这里笔误了。