如何基于扫描图像数据创建和优化网格

你有没有想过使用三维成像技术获得的数据创建网格？这篇文章，我们将讲解如何使用 COMSOL Multiphysics^® 软件来实现这一目标，这个主题是对上一篇博客中讨论过的不规则形状模拟主题的扩展。今天我们将讨论的过程，一部分已经在为拓扑优化结果设置验证研究时使用过。这篇文章，我们将对此工作流程进行概括，以适用于通过三维成像技术获得的数据。

输入的数据

COMSOL Multiphysics^® 支持导入不同格式的数据： txt 文件、Excel 文件、CSV 文件、图像、DEM 文件、MATLAB^® 函数，以及用 C 语言编写的外部函数。扫描的数据通常以一组横截面图像的形式出现，比如接下来我们将要介绍的示例中的数据：人体股骨的一部分。这个模型中的某些数据来自 Visible Human 项目。但是，COMSOL Multiphysics 只支持导入一张图像生成二维数据。因此，在使用软件之前，通过以下步骤生成数据文件：手动挑选带有股骨上半部分的图像，手动识别包含一根股骨的像素以减少数据量。随后，将识别出的像素亮度，连同它在空间中的位置一起读取和写入一个 txt 文件。图像中的像素位置用 x 坐标和 y 坐标表示，图像编号用 z 坐标表示。这些数据适合使用电子表格的格式保存，因为每个像素都是从图像中读取并逐一写入 txt 文件的：

x1 y1 z1 data1
x2 y2 z2 data2
x3 y3 z3 data3
...

此外，还对这些数据进行了清理，以删除股骨以外的所有信息，并根据股骨的实际尺寸进行了调整。同时为了方便使用，还对数据进行了二值化处理。

用于创建网格的人类股骨的二值化数据的三个切面图。白色代表数据文件中的亮度值为 1，黑色代表亮度值为 0。

此模型的 MPH 文件可以点击文末链接下载，这里仅对需要采取的步骤做一个大致的描述。在这篇文章的最后，我们将给出两个包含周围域的人类股骨的网格，可用于进一步的计算。我们还将讨论如何添加其他计算域和划分表面网格，以便能够在网格上应用适当的边界条件。

首先，将数据导入软件的一个 插值 函数中，并将其命名为 human_femur。我们将通过两种可能的工作流程来获得股骨的网格：

1. 一个快速通道，通过这个流程，可以获得非常粗糙的网格来表示数据，并允许重新划分网格使粗糙的表面变平坦。
2. 2. 一个包含更多步骤的工作流程，使用亥姆霍兹平滑来确保获得一个平滑的形状。

工作流程 1：使用网格数据集表示数据，并将表面重新划分网格作为一种平滑技术

我们先来看更快速的工作流程。在这个示例中，我们将使用 栅格 数据集表示数据，并使用 过滤器 数据集滤除数据来表示股骨。这个过程将产生一个比较大的表面网格，因此使用 自由三角形 操作对不平整的表面进行平滑处理。

设置网格数据集和过滤股骨数据

在这个工作流程中，我们不需要 几何 节点，甚至不需要模型开发器中的 组件 节点，稍后我们将在添加额外的计算域和创建股骨的计算网格时添加一个组件。在 全局定义 节点下设置 插值 函数，然后直接进入 结果，定义 栅格 数据集。

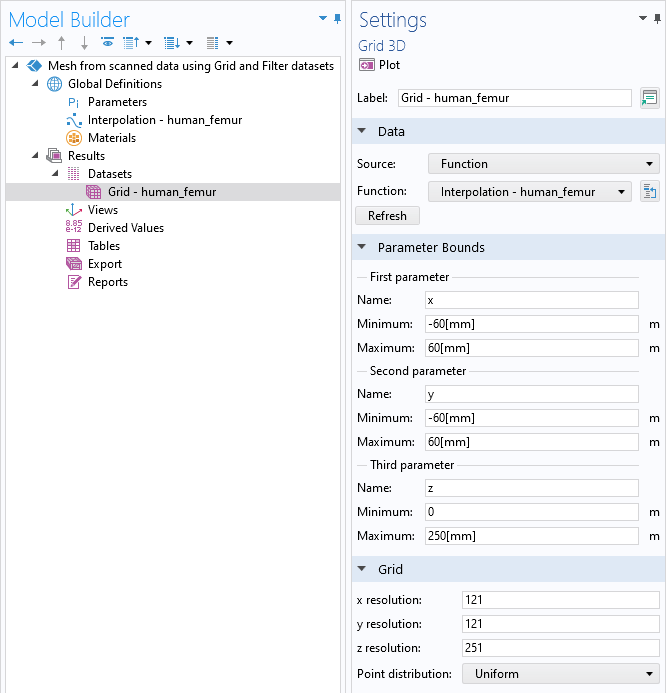
添加 插值 函数后，直接设置栅格数据集。

COMSOL Multiphysics UI 显示了模型开发器，突出显示了网格数据集功能，相应的设置窗口与数据，参数边界和网格部分展开。

将 栅格 数据集作为一个规则的网格使用，并在这个网格上应用 插值函数。此处，大约一半的图像分辨率被用作数据集的分辨率。接着，添加一个过滤器 数据集，输入表达式 human_femur(x,y,z)，并将 下限 设置为 0.99。这将创建一个值为 0.99 的等值面，并包含所有超过该值的数据。换句话说，就是创建一个人类股骨的等值面。如果最终想创建一个域，可以使用 过滤器 数据集。在第二种工作流程中，将使用 分割 数据集，你可以在其中定义多个值来创建多个等值面，这最终将产生多个计算域。

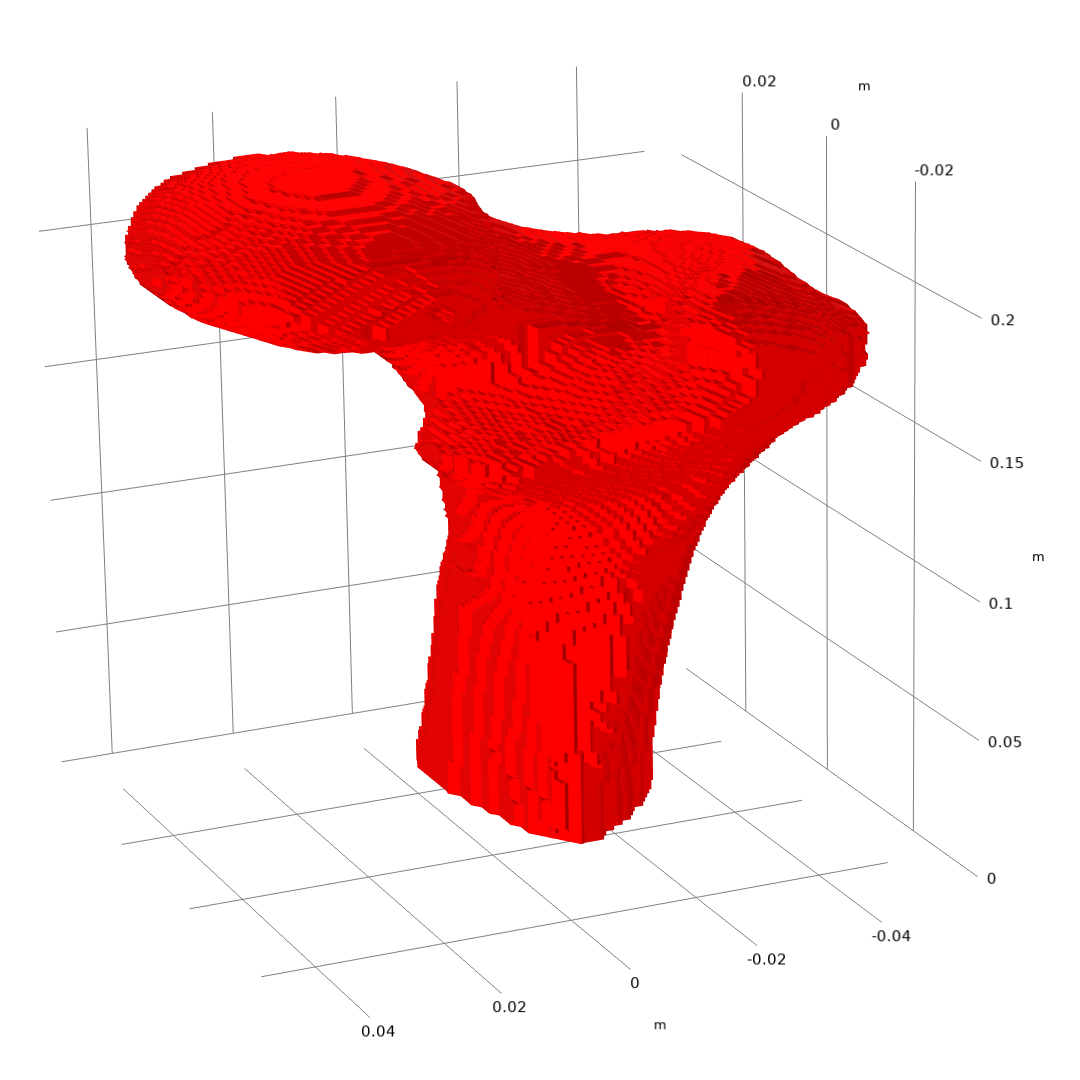
由 过滤器 数据集生成的等值面。请注意，由于坐标轴进行了缩放，股骨在 Z 方向上被压缩。

导入和分割过滤器数据集的网格

将 过滤器 数据集代表的网格导入网格划分序列中，并重新划分面网格以平滑粗糙度。通过右击 数据集 > 过滤器 节点，选择 创建网格零件 可以完成这个工作流程。

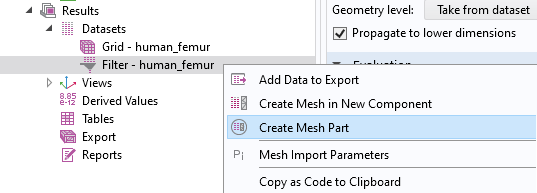
在第二个工作流程中，我们将使用 在新组件中创建网格 选项。选择创建一个 网格零件，因为稍后将使用这个网格作为构造几何。这一操作将在 全局定义 下自动设置一个网格零件，并添加一个 导入 节点，用于导入 过滤器 数据集的网格。过滤器 数据集的域单元质量通常较差，所以只导入三角形网格。然后，只要表面网格质量达到要求，将重新生成四面体网格。

在模拟中，经常需要进行特定的边界分割来应用边界条件。使用 与平面相交 操作切割平面，或者使用分割操作分割几何形状。 你可以通过阅读在 COMSOL Multiphysics^® 中编辑和修复导入的网格，了解相交和分割操作的不同。这里，我们将使用 用球分割 操作来获得一个大致的圆形边界。

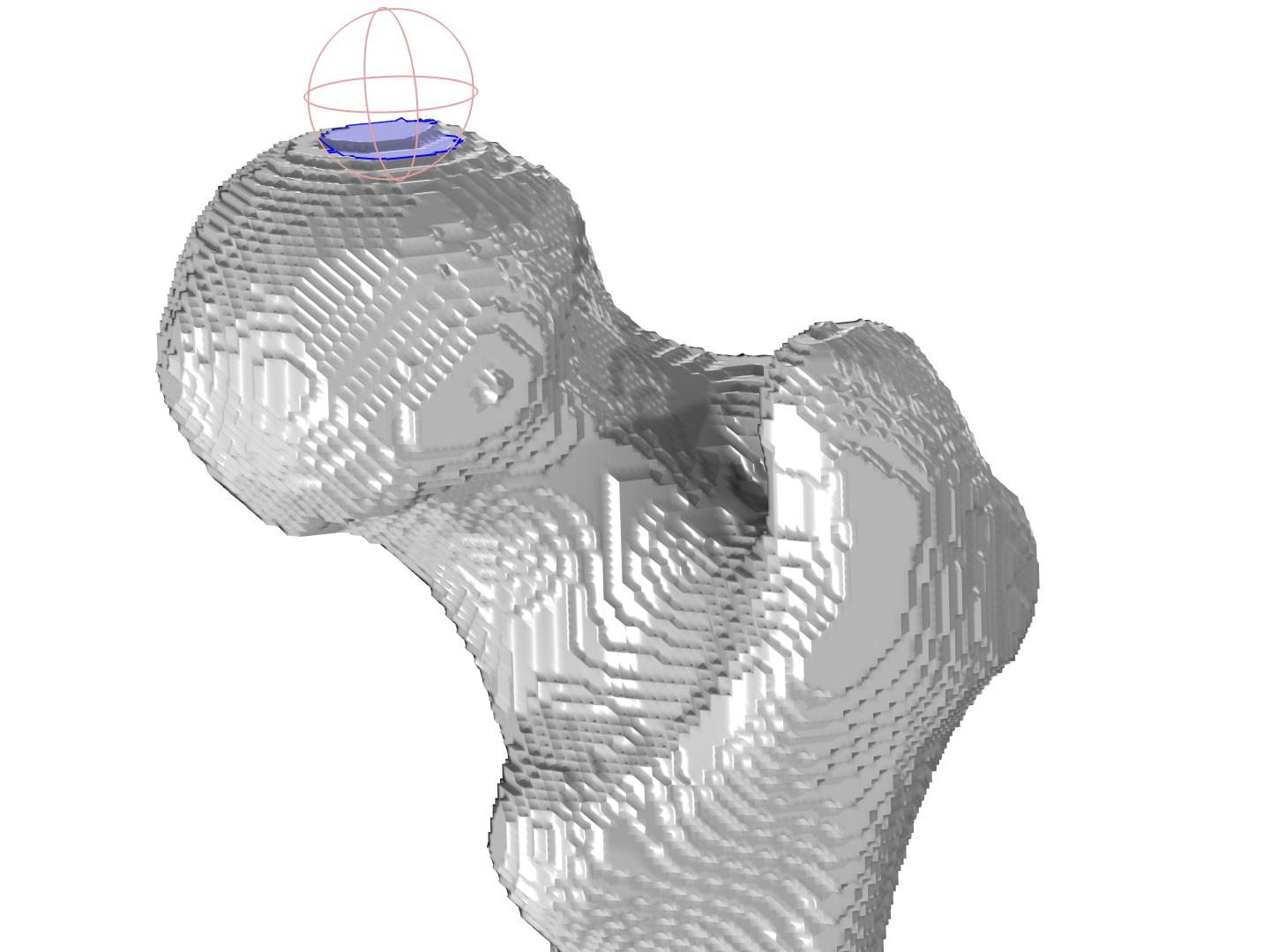
用 球分割操作（粉红色边）分割出一个大致的圆形边界（用蓝色突出显示），之后在这个边界上施加一个边界条件。为了便于观察，关闭了网格渲染。

重新划分网格以提高质量和平滑粗糙度

由于单元大小不一，并且有许多长条状的三角形，导致表面不光滑不适合模拟。因此，在使用之前需要对网格进行重新划分。使用更大的网格大小重新划分面网格，也可以平滑形状。

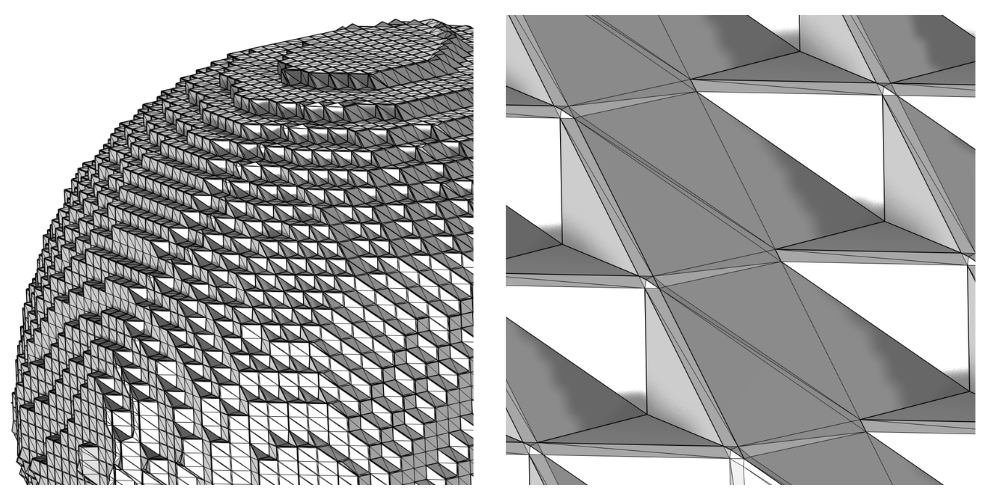
导入的 过滤器 网格放大图片。由于网格数据集是六边形，网格形状呈明显的块状，包含大三角形、小三角形和长条形三角形。

使用 对面重新划分网格 操作对面重新划分网格。为了避免求解网格中的粗糙度，对网格进行均匀化操作，设置一个大于原网格不均匀度的单元大小。具体可以通过将 最大单元大小 和 最小单元大小 设置为 0.005m 来实现。如下图所示，现在的表面已经足够平滑，但仍然有些不均匀。在稍后工作流程中，我们将再次重新划分边界网格，以进一步提升不规则面的均匀度。

图片显示了重新对表面划分网格之后的股骨顶部。

如果你正在尝试对几乎相交的表面重新划分网格，或者正在对那些几乎与自身相交的表面重新划分网格，可以试试亥姆霍兹平滑方法。

现在，表面网格已经足够均匀，可以继续在这个网格上添加额外的几何体。

添加更多的计算域

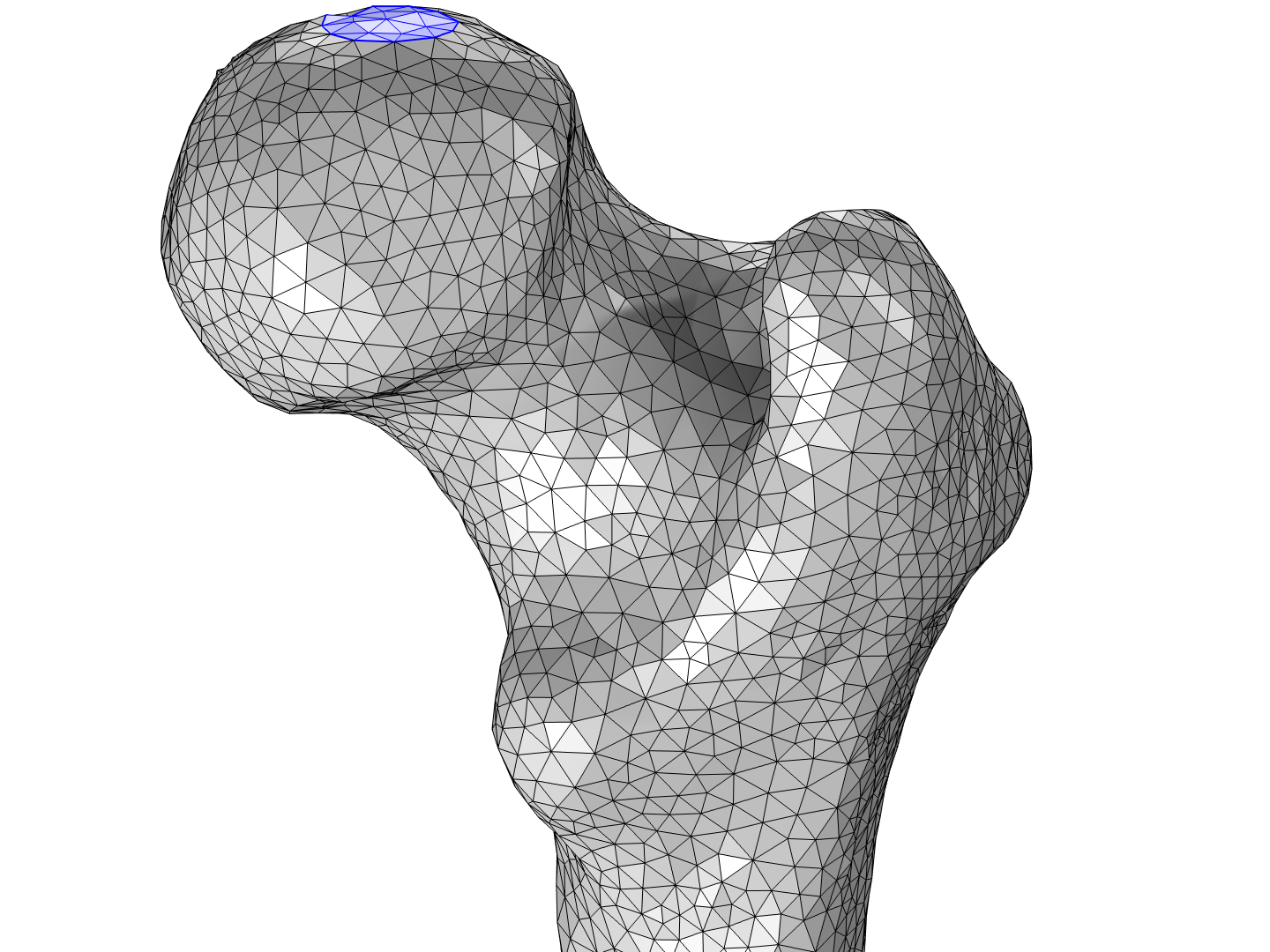
股骨域可能是你唯一感兴趣的区域，但假设你还希望在股骨周围再建立一个模拟域或一些螺钉来固定股骨中的裂缝，你会怎么做呢？这可以通过 几何 序列来实现。首先，在股骨模型上添加一个三维组件。然后，添加 几何>导入节点，在设置窗口中选择 网格零件 1。这个节点允许用户添加和定位新的几何体，并且应该被标记为 构造几何，因为我们将只使用股骨的面来定位新的几何体。一旦确定最终几何，构造几何对象就会被移除。你可以看到它是一个构造几何，因为它的边是虚线而不是实线。

将股骨作为 构造几何 对象导入几何序列，以定位与股骨有关的其他几何体。

将创建的几何体在网格划分序列中与网格相结合。在网格序列中，使用 并集 操作将几何体或导入的CAD与网格相结合通常是最稳健的方法， 这也是本文接下来要遵循的工作流程。

你可以画出在仿真过程中所需的任何几何形状，或者导入 CAD 设计。使用构造几何，可以很容易地绘制出所需的几何形状。在这个例子中，我们将添加两个螺钉来加固股骨，但无论是创建还是导入一个或多个几何对象，原理都相似。螺钉的几何形状和股骨的构造几何如下面的左图所示。创建完几何结构，并且已经构建完 形成联合体，股骨的构造几何就会从生成的几何结构中被移除，只剩下螺钉，如下图中间所示。对于导入的 CAD 设计，在将其与网格结合之前也可以添加 移除细节 或 虚拟操作 ，对几何体进行简化。关于如何将几何体和网格相结合的更详细的说明，请看查看STL 导入教程系列教程的第二部分。

在同一个 组件 中，转到 网格 序列。确保添加两个 导入 节点，一个导入螺钉的几何结构，另一个 导入 节点从网格部分（下图右）导入股骨的网格。使用网格 并集 操作将两个表面网格结合起来，并使用连接实体 节点将螺钉的域连接起来，因为它们被股骨的表面分成了两部分。

左图：螺钉的几何结构与股骨的构造几何对象。中间：构建 形成联合体 节点后的螺钉的几何形状。右图：导入到网格划分序列中的股骨和螺钉的网格。

使用 对面重新划分网格 节点重新划分股骨的表面，将 最大单元大小和 最小单元大小 设置为 0.005 m。请确保为 对面重新划分网格 操作添加一个 固定网格 属性，并选择保持螺钉孔边缘的网格固定（如下方左图中蓝色高亮部分所示）。这样可以提高螺钉孔周围网格的单元质量，并能进一步平滑股骨表面。

在保持螺钉孔周围边缘固定的情况下，第二次对股骨表面重新划分网格。

最后，添加一个 自由四面体 网格操作，用四面体单元填充整个域。若当前需要进行物理场分析，可以选择添加扫掠网格或边界层网格来优化。在设置和求解模拟时，将使用基于该网格定义的域和边界。

用高阶离散化添加物理场

现在，网格已经构建完成，可随时进行仿真，如下左图所示。但是，如果通过高阶离散化添加物理场，会发生什么？比如，我们想使用 二次巧凑边点单元 离散化设置建立一个固体力学仿真。弯曲单元的二阶节点将被放置在网格表面的弯曲表示上，类似于有基础几何结构时的放置方式。为了查看弯曲单元在网格中的样子，可以将网格数据集的 几何形函数 设置为 二次拉格朗日，和将网格绘图的节点设置为 几何形函数。二次拉格朗日 绘图 的设置并不与模型中的任何物理场离散化相耦合，它只用于绘图。

左图：股骨和螺钉的体网格图。白色单元代表螺钉的域，股骨的单元被表达式 x> -0.015 过滤掉了。右图：在股骨的弯曲边界上显示的具有二阶节点的最终网格。绿色和黄色代表偏度。

对比生成的网格和导入的数据

可以通过以下方式对比生成的网格如何跟随数据：添加一个用 栅格 数据集的网格分辨率绘制的 human_femur(x,y,z) 表达式的等值面图。从下图可以看出，生成的网格很好地遵循了等值面。

生成的表面网格（灰色）和插值数据 human_femur(x,y,z) 的等值面（蓝色）的对比。

工作流程 2：使用亥姆霍兹方程对股骨数据进行平滑处理

简单来说，在这个工作流程中，我们将添加一个应用股骨数据的规则块状域，然后通过求解亥姆霍兹方程对数据进行平滑处理，得到一个光滑的股骨表面网格。我们仍然需要对股骨表面重新划分网格，但这次只是为了提高网格单元的质量。

定义一个规则域

为了求解亥姆霍兹方程，我们需要定义一个域，可以是长方体、球体或其他一些简单的适用于股骨数据的几何形状，如这篇博客中所述。要确保这个域尽可能的小，这样就可以使用精细的网格来求解这个域。网格需要足够精细，以解析你想在表面网格中看到的任何数据中的细节。

定义了导入数据的规则域上的足够细的六面体网格。

接下来，我们来设置方程，添加一个瞬态研究并进行求解，以获得我们可以使用的解数据集。

对数据进行亥姆霍兹平滑处理

为了避免数值伪影，并有可能使用较粗的网格，使用滤波的亥姆霍兹偏微分方程（PDE）对插值函数进行低通滤波：

其中，R 是滤波器半径，近似代表低通滤波器的宽度。添加一个 系数形式偏微分方程 接口，如下图所示。

系数形式偏微分方程 接口的设置。

这里，我们使用表达式 max((h[1/m])^2,R^2) 来表示扩散系数。COMSOL软件会对网格中的每个节点使用最大的网格大小 h 和参数R。在这个例子中，局部的网格大小 h 是恒定的，但是如果使用非结构化的四面体网格，h 会变化。请注意，因为所有操作都是在一个由网格（每个单元网格都是线性）表示的几何结构上进行的，所有的单元离散化阶次被都降低到线性单元。然后使用一个稳态求解器计算解。

在六面体网格上绘制的插值函数 human_femur 的切面图（左）和平滑处理后的解数据（右）。

使用分割数据集过滤股骨

在平滑的解数据中使用一个介于 0（蓝色）和 1（红色）之间的值来过滤股骨的表面网格。在这个例子中，假设我们也希望股骨外的区域成为我们模拟的一部分，因此应该选择添加一个 分割 数据集。如果只对模拟股骨域感兴趣，可以使用 过滤 数据集，就像第一个工作流程中那样。水平值 为 0.6的 分割 数据集就已经足够满足我们的目标了，如下图所示。

分割 数据集的图，水平值设置为 0.6。等值面将模拟域划分为两个域，一个是股骨域，一个是股骨周围的域。

当对水平值满意时，右击分割 或 过滤 数据集节点，选择 在新组件中创建网格。如果需要创建额外的模拟域，请使用 创建网格组件 选项，并按照第一个工作流程的步骤进行。

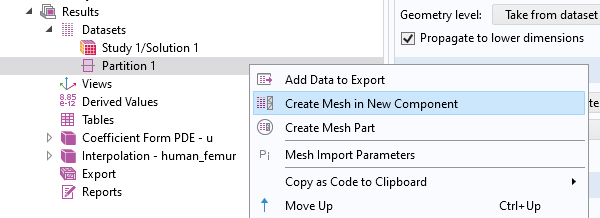
这将自动设置一个带有 导入 节点的新组件，用于导入 分割 数据集的网格。清除 导入域单元 复选框，并将 边界分割 设置为最小值，仅导入表面网格，形成尽可能少的边界；7 个平面边界和 1 个股骨边界。接下来，对这个表面网格进行改进，然后重新创建一个体网格。

导入的 分割 数据集网格。股骨的表面网格包含了大大三角、小三角和长条三角形，其质量需要提升以适用于模拟。为了便于观察，隐藏了一些边界。

重新划分表面网格来提高三角形的质量

使用 对面重新划分网格 操作对同一网格划分序列中的表面重新划分网格。为了得到大小基本相同的三角形，将最大单元大小 和 最小单元大小 都设置为 0.005m。

重新划分网格后的股骨和长方体表面。网格大小已经被修改，以生成一个大小基本相同的三角形表面网格。为了便于观察，隐藏了一些边界。

现在，我们可以用一个四面体网格来填充这些域。添加的物理场接口将被应用到这个网格所定义的域和边界上。这样，我们就有了高质量的体网格，可以用于仿真其他形状和应用，还可以在域中添加扫掠和边界层网格，但在这个例子中，四面体网格已经满足我们的需求了。

左图：股骨和周围长方体的体网格。白色的单元代表股骨域，周围的单元使用表达式 x > 0 过滤。右图：在股骨的弯曲边界上显示二阶节点的最终的网格。颜色代表偏度。为了便于观察，隐藏了一些边界起来。

对比生成的网格与导入和平滑的数据

在这个工作流程中生成的网格可以与导入的数据等值面 human_femur(x,y,z) 进行对比，该等值面与分割数据集使用的等值面相同，被绘制在原始长方体域的网格上。为了生成一个更接近导入数据的网格，可以在求解亥姆霍兹方程的原始长方体域中使用更细的网格，相应的也可以降低扩散系数。

生成的表面网格（灰色）和插值数据 human_femur(x,y,z) 的等值面（蓝色）对比。

结束语

至此，这篇由扫描的数据创建表面网格的文章就结束了。文中对表面网格进行了分割，使用了两种不同的方法对扫描数据进行了平滑处理，并介绍了如何将网格和几何结构结合起来。

如果您想要了解文中讨论的工作流程的更多细节，请点击下列按钮下载 MPH 文件。

更多资源

• 阅读在 COMSOL Multiphysics^® 中编辑和修复导入的网格博客，了解更多关于网格划分的内容。
• 在 STL 导入系列教程中了解更多关于编辑和重新划分导入的网格信息。
• 阅读“如何基于高程数据模拟不规则形状并构建几何模型”博客，查看另一个可以创建表面数据的例子。
• 阅读如何检查 COMSOL Multiphysics^® 中的网格博客，了解检查网格的三种方法。

文中介绍模型的一些数据来自 Visible Human Project，https://www.nlm.nih.gov/research/visible/visible_human.html，由美国国家医学图书馆提供。这些数据是截至 2023 年 4 月 21 日的最新数据，已经经过修改，可能无法映 NLM 提供的最新/最准确的数据。NLM 没有认可 COMSOL 的产品、服务或应用，并声明对数据的准确性或完整性不作任何明示或暗示的保证，包括对商业性或适用于特定目的的保证。数据的使用者应使 NLM 和美国政府不承担因数据错误而引起的任何责任。对于因使用、误用或解释数据中包含或不包含的信息而造成的任何后果，NLM 不承担任何责任。

MATLAB 是 The MathWorks, Inc. 的注册商标。