
在之前的文章中,我们介绍了一些涉及静止固体耦合传热的应用。这些静止固体传热示例对将要求解的传热方程进行了简化处理,并且通常可以得到求解温度场的精确近似。当涉及传热和固体力学的多物理场耦合时,如何描述用于解释材料热弹性效应的相关物理场? 阅读今天的文章,了解更多内容。
材料和空间坐标系
在介绍物理场之前,我们先简要回顾一下 COMSOL Multiphysics 中使用的坐标系。当考虑几何非线性时,固体力学 接口会区分材料 坐标系和空间 坐标系。材料坐标系以初始状态的坐标 \mathbf{X}= (X, Y, Z) 表示物理量,而空间坐标系以当前状态的坐标 \mathbf{x}=(x, y, z) 表示物理量。
下图展示了一个承受压缩应变的正方形几何示例。该正方形长 10cm,其左下角最初位于 (X, Y) = (1~\textrm{cm}, 1~\textrm{cm}),之后其左右两侧受到边界载荷的压缩而发生变形。此变形会使正方形上几乎所有点的位置发生改变。例如,左下角移至新的位置 (x, y) = (1.54~\textrm{cm},0.82~\textrm{cm}) 。
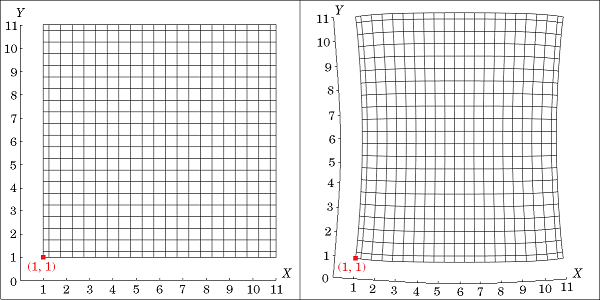
用材料坐标表示的变形的正方形,左侧为初始状态,右侧为最终状态。
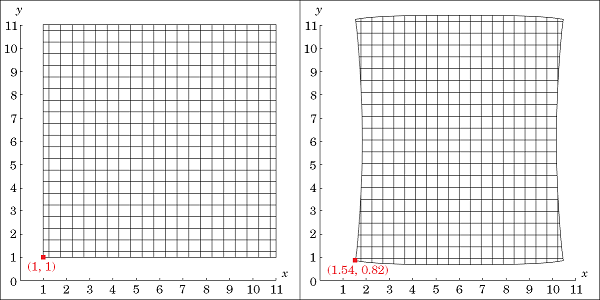
用空间坐标表示的变形的正方形,左侧为初始状态,右侧为最终状态。
材料坐标始终指时间上的同一质点,它最初位于指定点 (X, Y, Z)。固体力学的动量方程在此坐标系中建立。另一方面,空间坐标系中的点 (x, y, z) 是指当前状态下可能位于该点的任何质点,热方程在该坐标系中建立。
在这两个坐标系中,与体积相关的物理量具有不同的值。例如,在没有任何质量源的情况下,材料坐标的密度在变换之前和之后保持恒定,而空间坐标的密度随体积变化而变化。因此,为了将在材料坐标(结构力学)上建立的方程和在空间坐标(传热)上的建立另一个方程耦合起来,需要在每个坐标上合理评估这些值。下表列出了一些从材料坐标到空间坐标的热物理量转换。这些转换涉及变形梯度 \mathbf{F} = {\partial \mathbf{x}} /{\partial \mathbf{X}} 及其行列式 J 。二者均使用由固体力学 接口计算的位移场评估。
| 物理量 | 材料坐标 | 空间坐标 |
|---|---|---|
| 温度 | T | T |
| 密度 | \rho_0 | \rho = J^{-1} \rho_0 |
| 导热系数张量 | \bold{k}_0 | \mathbf{k} = J^{-1} \mathbf{F}\mathbf{k}_0 \mathbf{F}^T |
| 热弹性阻尼 | W_{\sigma, 0} = \boldsymbol{\alpha} T :\frac{\mathrm{d} \mathbf{S}}{\mathrm{d} t} | W_\sigma = J^{-1} W_{\sigma, 0} |
| 热源 | Q_0 | Q = J^{-1} Q_0 |
从材料坐标到空间坐标的热物理量转换。
这些转换还反映了一个事实,即应力和应变会通过修改几何结构(如空间坐标所示)影响传热。例如,延伸的边界更可能接收更多辐射热量(Q_\mathrm{r} > Q_{\mathrm{r}, 0}), 如下图所示。
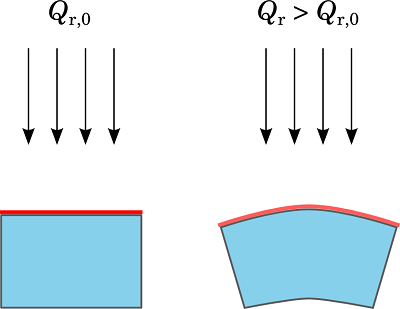
固体上表面接到的辐射热通量,初始状态(左)和拉伸上表面后(右)。
另一个示例是空间坐标中的导热系数表达式,通常使用初始状态值 \bold{k}_0,以及和固体应变有关的数量 \mathbf{F} 和 J 。
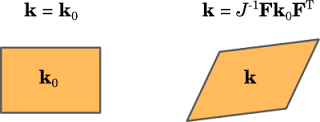
固体变形后,空间坐标上导热系数的变化。
与温度相关的应力和应变
固体力学方程是在材料坐标中定义的。通过线性动量平衡方程和应力-应变关系将位移 \mathbf{u}、第二类皮奥拉-基尔霍夫应力张量(second Piola-Kirchhoff stress tensor)\mathbf{S},以及弹性应变张量(elastic strain tensor) \mathbf{E}_\mathrm{el} 相关联。
(1)
(2)
其中,\mathbf{C} 是弹性张量,通常由杨氏模量和泊松系数定义。对于碳素结构钢 1020,该量可能与温度有关。
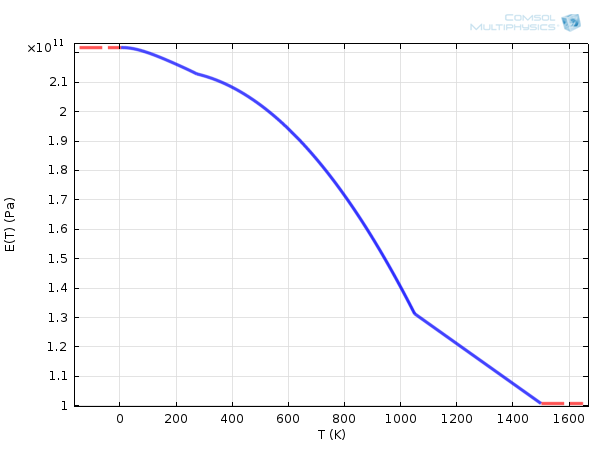
碳素钢结构 1020 的杨氏模量与温度有关。
下列公式说明,在没有任何塑性效应的情况下,弹性应变张量 \mathbf{E}_\mathrm{el} 通过热应变张量 \mathbf{E}_\mathrm{th} 传递温度相关性:
(3)
(4)
\mathbf{F}^\mathrm{T}-\mathbf{I})
(5)
热膨胀系数 \boldsymbol{\alpha},表征材料由于温度变化而收缩和膨胀的能力。通常是标量,但可能更常采用张量的形式。下表列出了各向同性 \boldsymbol{\alpha} 的一些典型值。
| 材料 | 热膨胀系数(10-6K-1) |
|---|---|
| 丙烯酸塑料 | 70 |
| 铝 | 23 |
| 铜 | 17 |
| 尼龙 | 280 |
| 石英玻璃 | 0.55 |
| 结构钢 | 12.3 |
一些材料的热膨胀系数。
此外,\boldsymbol{\alpha} 本身也与温度相关,如下例所示。
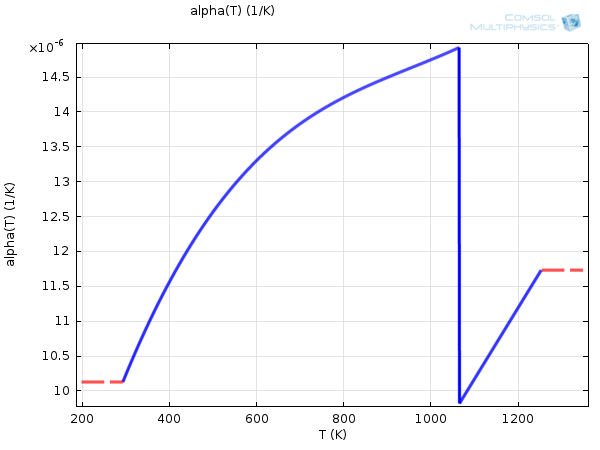
碳素结构钢 1020 的热膨胀系数,与温度相关。
从这些示例中可以看出, \boldsymbol{\alpha} 的值通常在 10-5 K-1 数量级。因此,为了使 \mathbf{E}_\mathrm{th} 变得显著,必须与参考温度有较高的温差。例如,铝需要达到高于参考温度约 500K 才具有 1.2% 的热伸长率。
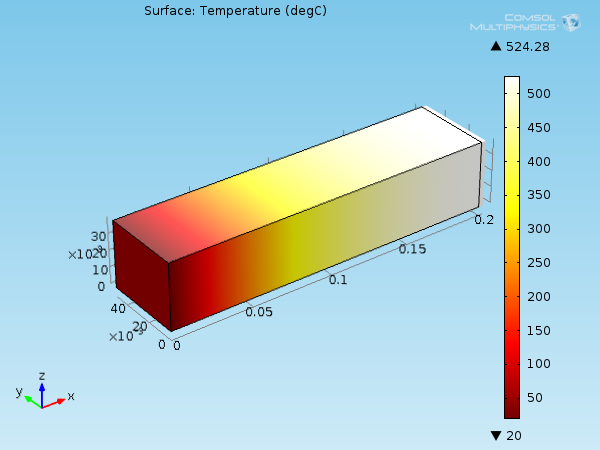
加热至 500K 的受约束的铝制横梁的热膨胀示例,采用 1:1 变形比例。
注意,在等式 (3)-(5) 的公式中,热应变是从总应变中减去的。由于热应变的值通常较小,因此对于小应变(通常为热应变)来说,这是一个合理的近似。适用于较大热应变的更精确的乘法公式如下所示,后文不再讨论。COMSOL Multiphysics 中的超弹性材料中采用的就是这种计算方法。
(6)
_\mathrm{el}\mathbf{F}_\mathrm{el}^\mathrm{T}
-\mathbf{I})
(7)
(8)
变形固体的热方程
热方程是由热力学第一定律推导出的能量平衡方程。对于固体,在空间坐标上采用以下形式:
(9)
耦合项 W_\sigma 是由于固体压缩或膨胀而产生的热源,其定义为:
(10)
式中,由于 \boldsymbol{\alpha} 与温度无关,可以简化为:
(11)
式中 \boldsymbol{\alpha} 是和 \mathbf{E}_\mathrm{th} 表达式一样的热膨胀系数。如上表所示,低的 \boldsymbol{\alpha} 值必须通过足够高的 T {\mathrm{d} \mathbf{S}} / {\mathrm{d}t} 值作为补偿,以使 W_\sigma 成为重要的热源,即:
- 在高温下
- 通过快速和高度变化的应力
下列为描述传热与固体力学多物理场耦合的 4 个关键贡献:
- 应变和应力对材料或空间坐标中的热量和边界热通量的影响
- 与温度相关的弹性矩阵
- 通过热应变张量与温度相关的弹性应变张量
- 热源 W_\sigma,对应于固体中的热弹性阻尼
接下来,我们将解释最后 2 个耦合贡献,并将通过几个仿真示例来展示如何在 COMSOL Multiphysics 中处理它们。
示例 1:涡轮静叶片中的热应力
我们之前的博客中曾详细地描述了如何模拟涡轮静叶片中的热应力。在这里,为了显示 J_\mathrm{th} 的影响,我们只展示了结果。因为这是一个稳态模型,所以可以忽略热弹性阻尼 W_\sigma。
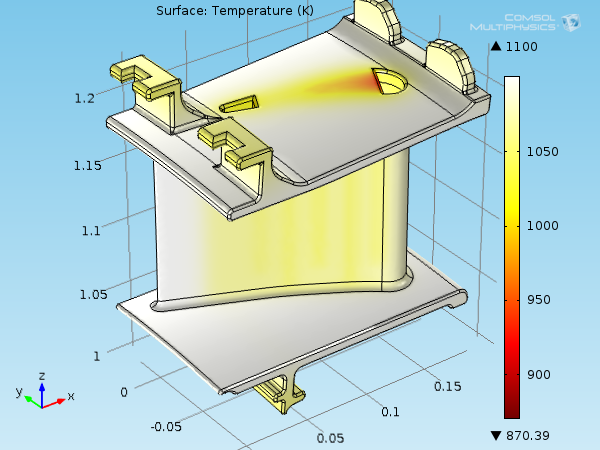
在材料坐标中表示的叶片表面温度场。
由于处于高温环境,与最初静叶片形状的参考温度 300K 相比,温度场的值介于 870K 和 1100K 之间。如此高的温度更容易使材料发生热变形。平均热膨胀系数和温度约为 1.2·10 -5 K -1 和 1070K,\mathbf{E}_\mathrm{th} 在 0.9% 左右。
对于大变形,热效应导致的体积膨胀为 \Delta V/V_0 = J_\mathrm{th}-1(J_\mathrm{th}
在等式(8)中被引入)。对于小应变,它仍然是一个很好的近似值,约产生 2.80% 的膨胀。在结果与可视化中,实际的体积膨胀为 2.76%。
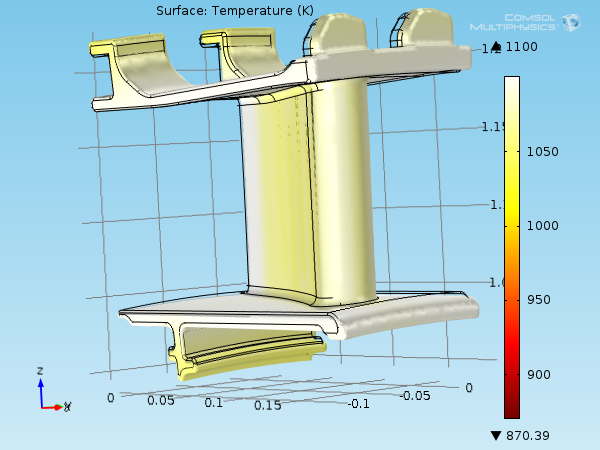
静叶片的温度场和变形,为了提高可见性,将绘图放大了 3 倍。
示例2:支架传热的瞬态分析
结构力学模块的模型库和 COMSOL 案例库中都提供了支架瞬态分析模型。在这个模型中,支架臂随快速瞬态载荷移动,温度将发生微小的变化。
现有模型忽略了这些热效应,因此,我们需要在固体传热 接口中增加新的传热。
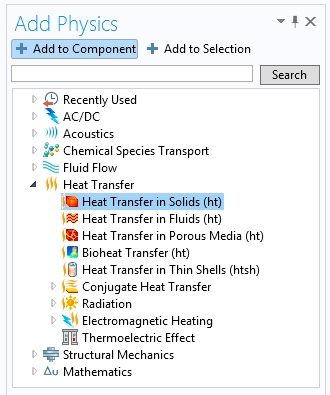
然后,添加以下两个多物理场特征,将固体传热 和固体力学 接口耦合起来:
- 热膨胀
- 用于修正施加在整个支架域上的热应变张量 \mathbf{E}_\mathrm{th} 和热弹性热源 W_\sigma
- 温度耦合
- 用于将通过固体传热 接口和固体力学 接口计算出的温度变量耦合在一起
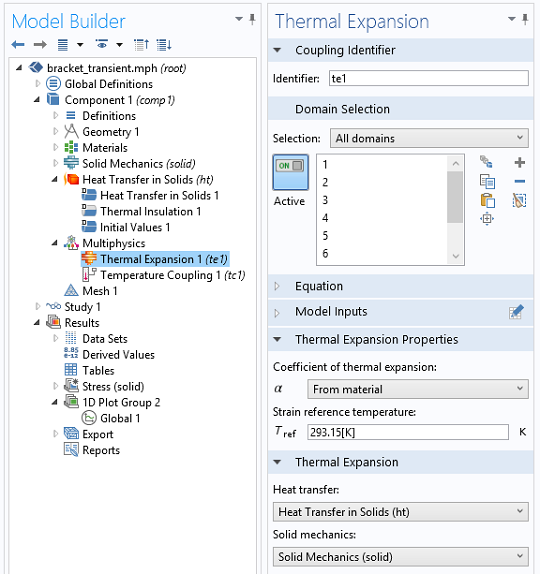
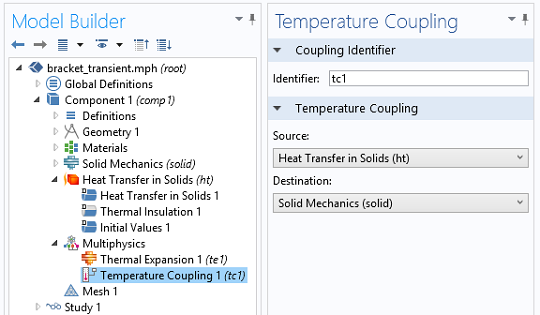
该研究还可以扩展到 30ms,以观察更多的载荷周期。
从各处的温度均为 20°C 等温剖面开始,微小的温度变化导致的热应变张量可忽略。现在,对热效应的主要贡献为由快速应力变化引起的热弹性热源。
随时间变化的支架温度分布,为了提高可见度,将绘图放大了 10 倍。
在支架的极端温度之间可以观察到约 0.8K 的差异。与预期相符,加热和冷却过程位于应力更重要且应力变化更大的拐角处。
通过求解热方程和动量平衡方程,变形固体中的热量传递可以通过数值计算得出。根据实际情况,对两个坐标系加以区分:
- 建立运动方程的材料坐标
- 建立热方程的空间坐标
两个坐标中与体积有关的数量具有不同的值,并且需要相互转换,特别是对于特定的能量和密度。
这两个控制方程均包含耦合项,用于使固体运动与温度相关,传热与固体变形有关。如前文中的两个示例所示,COMSOL Multiphysics 中提供了可以描述这些过程的合适的功能。
当温度保持在参考温度附近并且应力没有太快变化时,这些耦合效应可以忽略不计。否则,应将它们添加到模型的公式中。
如果要深入研究该主题,您可以下载文中提到的模型相关文件,并通过下面的链接阅读相关的博客。
更多资源
- 模型下载:
- 之前的博客文章:
编者注:为了与 COMSOL Multiphysics 5.1 版本保持一致,此博客已于 2015 年 7 月 23 日更新。



评论 (0)