
在流体流动仿真中,评估流体作用在固体上的力通常很重要,例如作用在汽车或机翼上的升力和阻力。通过计算这些体力,工程师可以量化设计的效率和空气动力学性能。今天,我们将讨论在 COMSOL Multiphysics 中计算升力和阻力的不同方法。
定义升力和阻力
当流体流过一个物体时,会在物体表面施加一个力。如下图所示,垂直于流动方向的分力称为升力,平行于流动方向的分力称为曳力。为简单起见,我们假设流向与模型的坐标系对齐。稍后,我们将向您演示如何计算与模型坐标系不对齐方向上的升力和阻力。
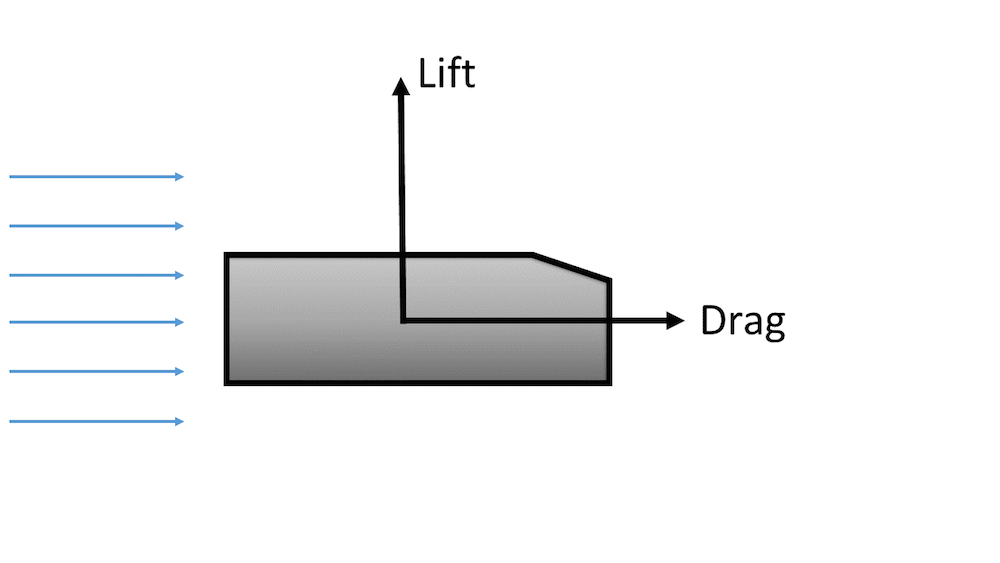
流体流过物体时,升力和阻力分量的示意图。
升力和阻力有两个不同的来源——压力和黏性力。压力 通常称为压力梯度力,因表面压差而产生。黏性力 是由与流体方向相反的摩擦力产生。压力和黏滞力的大小有很大的不同,具体取决于流体的类型。例如,行驶的汽车周围的气流通常是由压力控制的。
使用总应力计算升力和阻力
在 COMSOL Multiphysics 中,我们可以访问所有的内部变量,这使得通过边界积分来计算表面力变得非常简单。在这里,我们将演示如何计算 Ahmed 体上的阻力。您可以通过 COMSOL 案例库中下载这个模型。

Ahmed 体上方的气流仿真。表面图显示了压力分布,流线的颜色表示速度大小。Ahmed 体后方的表面箭头显示了尾流区的环流。
根据物理场,有几种方法可以计算阻力。最直接的方法是在计算每个方向上的积分总应力——包括压力和黏性力的贡献。为此,我们首先需要在“派生值”节点下定义一个表面积分算子,如下所示。
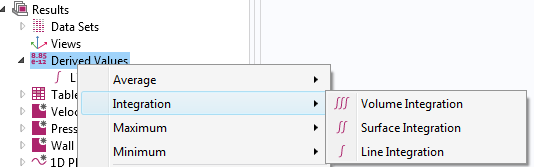
提示:另外,您也可以在组件耦合中使用边界探针或积分算子定义这种积分。不同之处在于,在物理场设置中定义的算子可用于仿真。例如,在优化研究中使用边界探针作为目标或约束来计算阻力。
接下来,我们可以选择边界进行积分。在这个例子中,我们选择了物体上的所有边界。此模型中的升力位于 y方向。我们可以输入表达式:spf.T_stressy,表示 y-方向上的总应力。
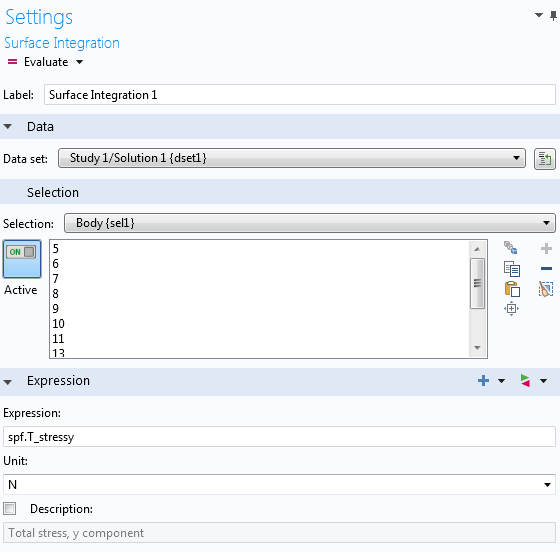
分别计算压力和黏性力
有时,工程师可以通过分别查看压力和黏性力获得对设计更深入的理解。对于y方向的黏性应力,COMSOL Multiphysics 提供了预定义的变量,spf.K_stressy。我们可以很容易地通过积分黏性应力来估算黏性力。
压力如何计算?由变量 p表示的压力是一个标量。为了向阻力方向投射,需要用压力乘以表面法向量 spf.nymesh 的 y分量。因此,我们可以通过积分 spf.nymesh*p 来评估表面上的压力。
在一些使用了壁函数的特殊湍流中,使用摩擦速度 spf.u_tau 计算黏性力更加准确。在 COMSOL Multiphysics 中,k-ε 和 k-ω 湍流模型使用壁函数。
如果需要了解更多关于 COMSOL Multiphysics 湍流模型的信息,请阅读博客:我应该为我的 CFD 应用选择哪种湍流模型?
可以通过以下方法获得壁的局部剪应力:
因此,y方向的局部剪应力可以表示为:
其中,u^T 是壁的切向速度。我们可以进一步将 u^T 重新写作 u_\tau*u^+,其中 u^+ 是切向无量纲速度。
我们无需在推导上花费太多精力,只需把前面的方程转换成 COMSOL 变量。我们可以使用表达式: spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus 对阻力方向(y方向)上的局部壁面剪应力积分。在这个表达式中,spf.rho 为流体的密度,spf.u_tangy 为壁在 y方向上的速度, spf.uPlus 为切向无量纲速度。
下面的表格总结了用于计算每个力的表达式。
| 无壁函数的流体流动 | 有壁函数的湍流 | |
|---|---|---|
| 压力 | spf.nymesh*p | spf.nymesh*p |
| 黏性力 | -spf.K_stressy | spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus |
| 总力 | -spf.T_stressy | spf.nymesh*p + spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus |
注意:在这个例子中,阻力在 y方向。您可能需要根据模型的方向更改投影方向。
攻角修正
通常,几何形状可能与流动方向不完全一致。几何中心参考线和入流之间的角度称为攻角 (通常用希腊字母\alpha表示)。在航空航天工程中,经常使用攻角,因为它是翼型弦线和自由流方向之间的夹角。下图显示了升力、阻力和机翼攻角之间的关系。
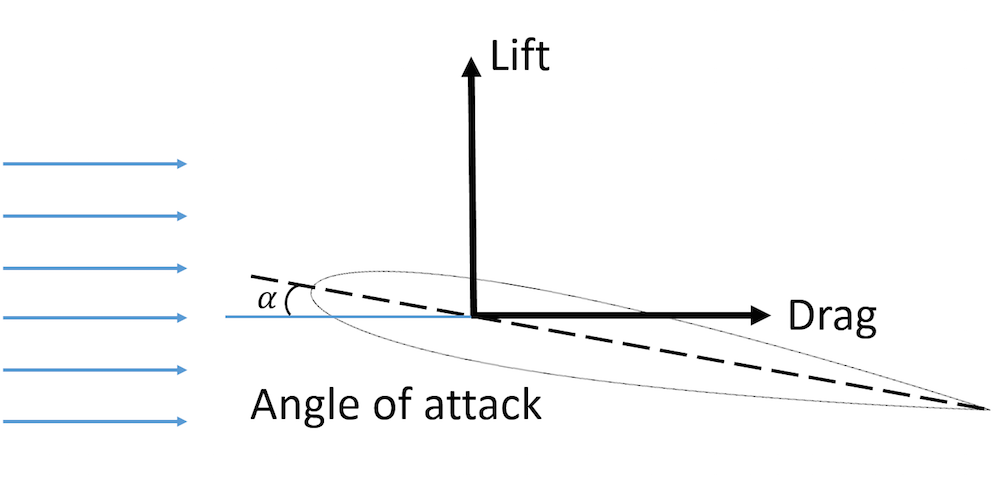
机翼上的升力、阻力和攻角的示意图。
以 2D NACA 0012 型机翼为例,我们将向您展示如何用攻角修正来计算升力。这个模型可以在 COMSOL 案例库中找到。
有两种方法可以改变模型的攻角。我们可以旋转几何结构本身,也可以保持几何结构不变,但需要修改入口处的流向。在这里,我们将使用第二种方法。调整进气道边界条件的速度场要简单得多,因为不需要为每个攻角模型划分网格。如下图所示,翼型是固定的,流线显示了由于调整进气速度方向而产生的攻角气流。
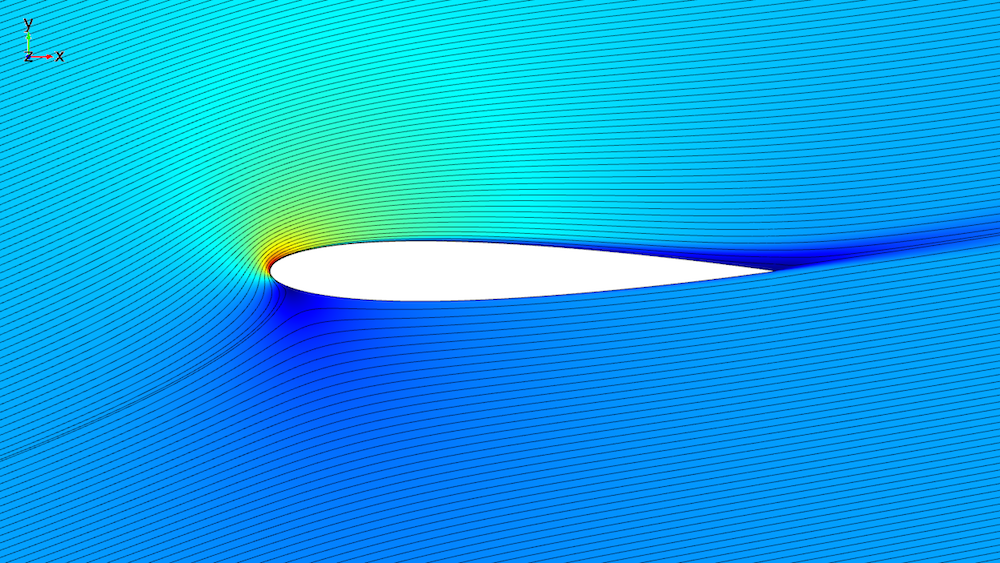
攻角为 14° 时,通过 NACA 0012 型机翼的气流模拟。表面图显示了速度大小以及流线(以黑色显示)。
这个示例使用了不包含壁函数的 SST 湍流模型。因此,我们将使用总应力来计算升力。在攻角为 0° 时,升力 -spf.T_stressy 很简单。如果攻角不为零,我们可以用下面的表达式将力投射到升力方向上: spf.T_stressx*sin(alpha*pi/180)-spf.T_stressy*cos(alpha*pi/180)。式中, alpha 表示攻角,单位为度。
如何计算升力或阻力系数?
你也可能对升力和阻力的无量纲形式,即升力系数和阻力系数感兴趣。为了验证实验数据或者对不同的设计进行比较,通常更容易使用系数来代替有量纲的力。二维的升力系数的定义如下:
既然我们已经计算了空间升力,就可以使用动态压力和弦长简单地将力无量纲化。利用无量纲的升力系数,可以将仿真结果与实验数据进行比较(参考文献1).
注:在三维模拟中,升力系数是按面积而不是按长度无量纲化的: C_L = \frac{L}{\frac{1}{2} \rho u^2_\infty A}
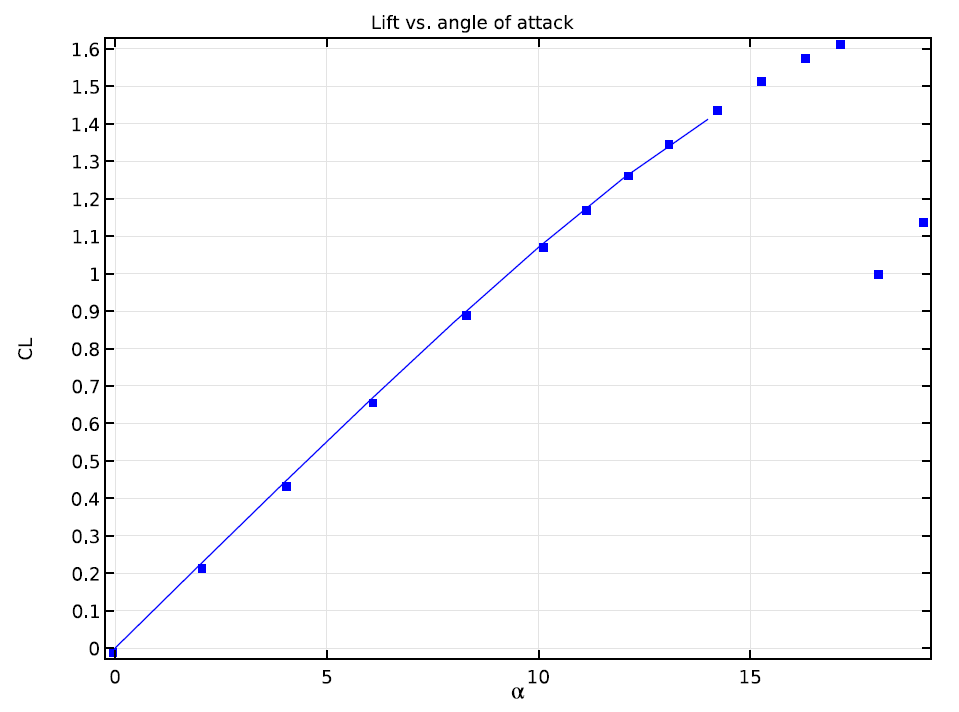
不同攻角时,NACA 0012 机翼升力系数的仿真结果和实验数据的比较。
如上图所示,在这个仿真中使用的攻角值范围内,计算结果和实验结果之间没有显著差异。实验结果继续朝机翼失速的攻角方向发展。
结束语
在这篇博客中,我们讨论了计算 Ahmed 体和 NACA 0012 机翼升力和阻力的方法,演示了如何计算压力和黏性力,同时还研究了在湍流模型中使用壁函数的特殊情况。
这里介绍的方法当然不限于这些特定的模拟,我们可以计算任何边界或表面上的力,从而通过多物理场仿真获得对设计的理解。使用优化模块,还可以通过更进一步的分析,优化升力或阻力。
参考文献
- C.L. Ladson, “Effects of Independent Variation of Mach and Reynolds Numbers on the Low-Speed Aerodynamic Characteristics of the NACA 0012 Airfoil Section,” NASA TM 4074, 1988.



评论 (0)