
作为一名技术支持工程师,我最常被问到的一个技术问题是:”我怎样计算流体流动仿真的质量守恒或共轭传热仿真的能量守恒?” 这通常是为了研究和确保仿真的准确性而提出的要求。在这篇博客中,我将演示如何在 COMSOL Multiphysics® 软件中进行这些计算,并介绍一些可以用来对能量守恒方程的能率项进行后处理的预定义变量。
让我们从质量守恒开始
为了演示这篇博客所涉及的不同主题,我将以一个铝制散热器为例,这个散热器通常用于通过散热来冷却电气设备。如果你有传热模块或 CFD 模块,可以在 COMSOL Multiphysics 案例库中找到这个教程模型的稳态版本。
该散热器由铝制成,集成了大量用于冷却的支柱,并安装在由硅玻璃材料制成的芯片上。在模型设置中,散热器位于一个矩形通道内,有一个气流的入口和出口。芯片作为一个热源,产生 1W 的热量。
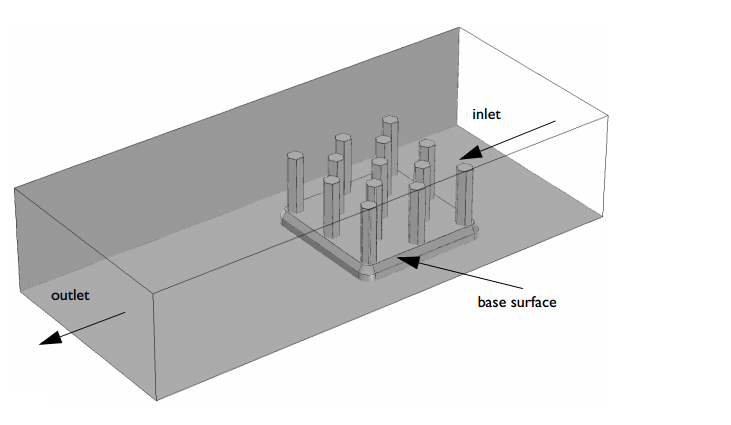
基本散热器的几何形状
在流体力学中,由质量守恒得到一个著名的局部连续性方程:
对该方程在流体域积分,应用散度定理,得到质量守恒的全局公式:
因此,
\rho{\bf{u}}\cdot {\bf{n}} \ dS = 0
我们来仔细看一下上面的方程。当你对流体流动进行建模时,可以计算这个方程,来检查你的模型的质量守恒准确性。在任何稳态分析中,这个方程简化为 \int_{\partial\Omega} \rho{\bf{u}} \cdot {\bf{n}} \ dS = 0,并指出,质量进入系统的速度等于质量离开系统的速度。换句话说,入口和出口的质量流动必须平衡。
一个常见的错误是,假设质量守恒可以简化为体积流动速率 \int_{\partialOmega}{\bf{u}}\cdot {\bf{n}} \ dS = 0守恒。如果流体密度是恒定的,如不可压缩流,连续性方程简化为 \nabla \cdot {\bf{u}} = 0,即流速的散度消失。在不可压缩流的情况下,这个假设是正确的。然而,在大多数工程问题中,这一假设是不成立的。粗略地说,在无运动边界的情况下,只要密度不依赖于任何可能导致密度沿流线变化的变量(如绝对压力、温度、浓度等),我们就可以考虑它。
也就是说,我们在 COMSOL Multiphysics 中检查流体流动仿真的质量守恒精度。为此,我们可以使用派生值 功能,这是一个有用的后处理功能,用于计算数据集中每个解的积分量。要创建一个派生积分值,首先进入结果 > 派生值 > 积分 > 表面积分 或体积积分。然后,选择应该进行积分的边界或体积。最后,输入要积分的表达式。
派生值 功能会生成一个带有数值的表格;你不能对不同的数值进行数学运算。因此,假设你想用一个数值减去另一个数值或计算比率,在定义 > 组件耦合 中定义积分运算符也很方便。这样,这些运算符就可用于数学表达式,并可在变量列表中的变量定义中自由使用。这样做以后,你就可以在派生值列表中展示它们。
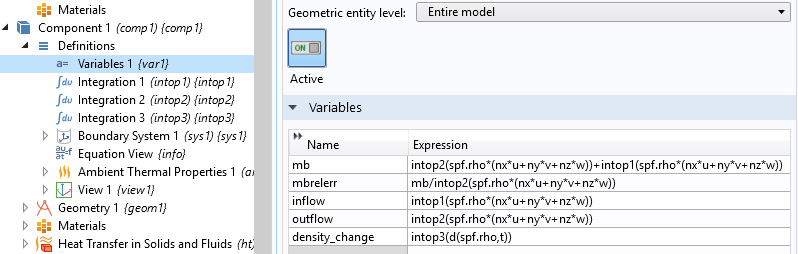
这里,进口和出口质量流量的表达式都被写成 spf.rho*(u*nx+v*ny+w*nz),如下图所示。spf.rho表示用于定义流体密度的变量;(u,v,w) 是速度场矢量;(nx,ny,nz) 是由 COMSOL Multiphysics 自动计算的选定边界的法向量。密度变化率可以表示为 d(spf.rho,t)。运算符 d 的目的是对一个变量相对于另一个变量进行求导。在这里,我们取的是流体密度的时间导数。
对质量守恒方程中的每个质量流率项进行分步骤计算。
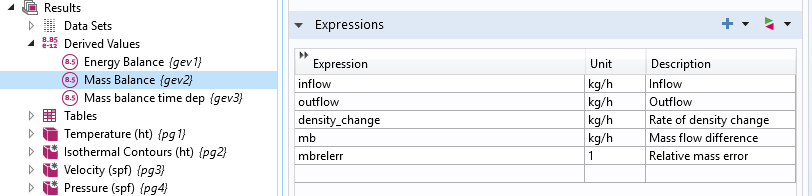
在散热器模拟的静态情况下,进口和出口边界的质量流动速率描述如下。入口和出口之间的相对质量差约为1e-5,小于求解器的相对容差设置,即设置为 0.001。因此,质量守恒是相当准确的。
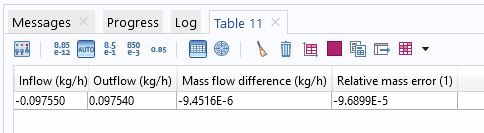
稳态研究的质量守恒结果。
我们还可以对同一模型进行稳态分析。仿真的总时间被设定为 20 分钟,在整个仿真时间内,散热器的底座承受了 1W 的热通量。求解器的相对容差被设置为 0.001。仿真结果可以在下面的动画中看到。我们将仿真时间设定为足够长,以达到热和流体流动的稳定状态。
流体流线用速度模着色,绘制了边界上的温度。
下图给出了瞬态分析的质量守恒结果。
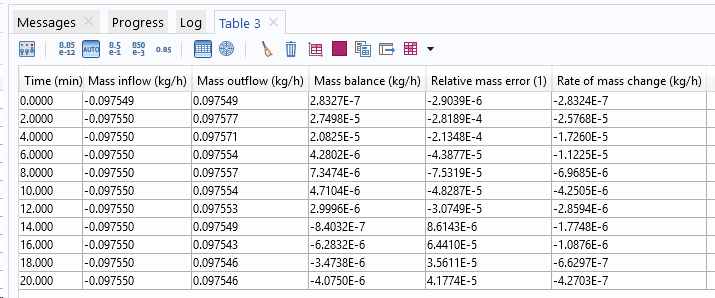
稳态研究的质量守恒结果。
精确性依然很好。
计算能量守恒
由热力学第一定律和力学定律,可以得出著名的全局热平衡方程。
这里,Q_\mathrm{{exchange}} 指换热率,考虑传导 热通量 -k\nabla T;辐射 热通量,{\bf{q}}\mathrm{{rad}} 和额外的热源 Q;如电磁热源(焦耳热),感应加热,或任何用户定义的热源。P_\mathrm{{stress}} 代表由力学应力引起的应力功率,E_\mathrm{{system}}=\int_\Omega E \ dm 是内部能量。
该方程中涉及的应力功率被转换为热耗散。应力功率表达式来自连续体力学理论,可写为
式中,\sigma 是柯西应力张量,{\bf{D}}= \frac{1}{2}(\nabla {\bf{u}} + \nabla {\bf{u}}^T) 是应变率张量。
对于流体,应力张量可以分为压力部分和黏性部分 \sigma=-p{\bf{I}}+\tau。然后,应力功率变为压力变化做的功和黏性耗散项的总和,如下所示。
在 COMSOL Multiphysics 中,我们可以选择添加这些效应中的一种、两种,或者都不添加。通过非等温流 多物理场节点,每个效应都有一个复选框,默认情况下是不被选中的。
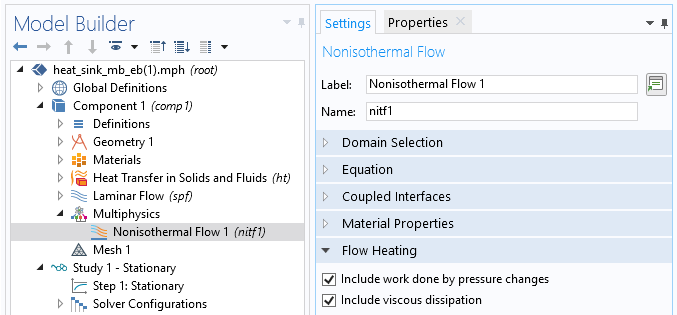
包括压力变化做的功和包括黏性耗散的特征。
对于共轭传热分析,即传热方程与纳维-斯托克斯方程和连续性方程一起求解时,以下总能量通量成为守恒量。
式中,E_0=E+\frac{1}{2}{\bf{u}}\cdot {\bf{u}} 是总内能。
总能量通量包括对流、传导和辐射热通量。它包含了代表对流动能的附加项 \rho\frac{{\bf{u}}}{2}({\bf{u}}\cdot {\bf{u}}),以及对流应力能 \sigma{\bf{u}}。能量守恒方程的形式如下:
\int_\Omega \rho E_0 \ dV +\int_{\partial\Omega} {\bf{e}}\mathrm{tot} \cdot {\bf{n}} \ dS = \int\Omega Q \ dV
在稳态研究中,这个表达式简化为
{\bf{e}}_\mathrm{tot}
\cdot {\bf{n}} \ dS = \int_\Omega Q_ \ dV
对于这个方程的每个量,都有一个预定义的全局变量可供后处理。得出的全局计算值可用于计算变量。下表总结了不同的相关预定义变量的名称。
| 总累积能率 | \frac{d} {dt} \int_\Omega \rho E_0 \ dV |
\mathrm {ht.dEi0Int} |
|---|---|---|
| 总净能率 | \int_{\partial\Omega} (\rho{\bf{u}}E_0-k{\bf{\nabla}} T+{\bf{q}}_\mathrm{rad}-\sigma{\bf{u}}) \cdot {\bf{n}} \ dS | \mathrm{ht.ntefluxInt} |
| 总热源 | \int_\Omega Q \ dV | \mathrm{ht.QInt} |
因此,使用 COMSOL Multiphysics 中的预定义变量编写的能量守衡方程为:
+ \mathrm{ht.ntefluxInt} = \mathrm{ht.QInt}
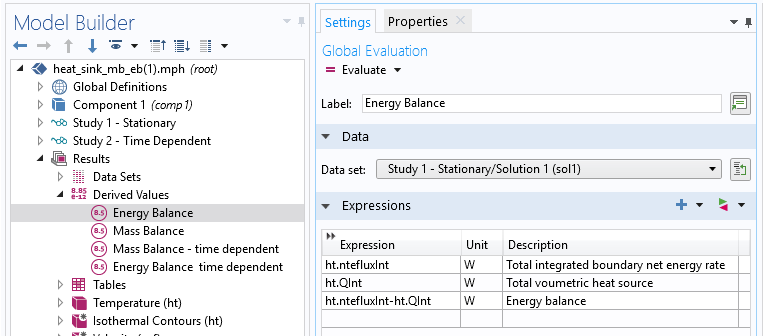
使用派生的全局计算值来计算预设变量的能量率。
在稳定状态下,总的累积能率消失了。总净能率和总热源必须守衡。稳态研究的结果显示如下。相对误差又远远小于相对求解器的容差。

稳态分析的能量守衡。总净能率和总热源必须守衡。
下面是瞬态分析的能率图。总净能率逐渐增加,最终达到稳态值,这平衡了散热器上施加的通量,1W。另一方面,总累积能率最初平衡了总的热源,一旦达到稳定状态就会消失。此外,粉红色的线表示能量守衡的绝对误差 \mathrm{ht.dEi0Int} + \mathrm{ht.ntefluxInt}-\mathrm{ht.QInt};也就是说,在最好的情况下,它应该是零。结果显示出良好的一致性。
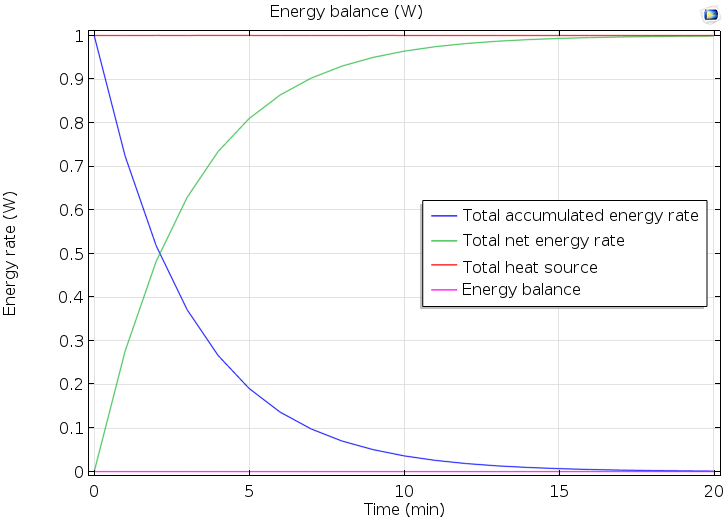
能率与时间的关系。
结语
这篇文章,我们讨论了稳态以及瞬态共轭传热问题的质量和能量守恒理论。还研究了如何用 COMSOL Multiphysics 计算能量和质量守衡,来检查仿真结果的准确性。为此,我们介绍了一些有用的派生值功能。预定义的能率变量很容易使用,可以避免自己手动进行能率表达式的计算。
我们使用了一个特定的例子来演示本博客所涉及的主题,但所演示的方法可以扩展到任何共轭传热问题。关于 COMSOL Multiphysics 中能量守衡的更多阅读内容,请查看传热模块的用户指南。
自己尝试
点击下面的按钮,进入 COMSOL 案例库。下载 MPH 文件,尝试自己动手模拟。
编者注:本博客于 2019 年 6 月 3 日更新,包括新的细节和更新的信息。



评论 (0)