机械系统中常常包含一些表现出非线性材料行为的部件。例如,密封件和垫圈中的大弹性变形、橡胶和生物软组织在承受循环载荷过程中的应变率依赖性和滞后性,以及金属中的弹塑性流动和蠕变。COMSOL Multiphysics® 软件及其附加的非线性结构材料模块包含 100 多个内置材料模型,可用于模拟高度复杂的材料行为。然而,这些模型(通常是现象学模型)有一个缺点,可能包含大量需要针对每种特定材料进行校准的材料参数,以获得准确的仿真预测结果。在今天的博客中,我们将介绍如何利用非线性最小二乘最小化方法,由从普通材料测试获得的实验数据对这些参数进行估计。
常见的材料测试
估计材料参数首先要获取相关实验数据。如上一篇博客所讨论的,相关数据在很大程度上取决于材料类型和最终应用中的预期载荷类型。例如,各向同性线弹性材料可以通过单轴测试进行表征。具有应变率和载荷-历史依赖性的材料则需要进一步的试验,如松弛、蠕变或不同应变速率下的循环试验。如果部件在高温和(或)不同的温度下工作,可能还需要考虑与温度相关的材料特性。
对于经历大变形的材料,即使材料行为是各向同性的,测试不同应力状态下的材料特性也很重要。与线弹性一样,虽然根据单轴测试校准超弹性模型很有吸引力,但在压缩或双轴载荷下对该模型进行预测,可能会产生意想不到甚至不稳定的材料行为。相反,校准橡胶类材料通常采用的试验组合包括单轴拉伸、纯剪切和等双轴拉伸试验。接下来,我们以一个橡胶薄板试样为例,来说明如何进行此类试验。
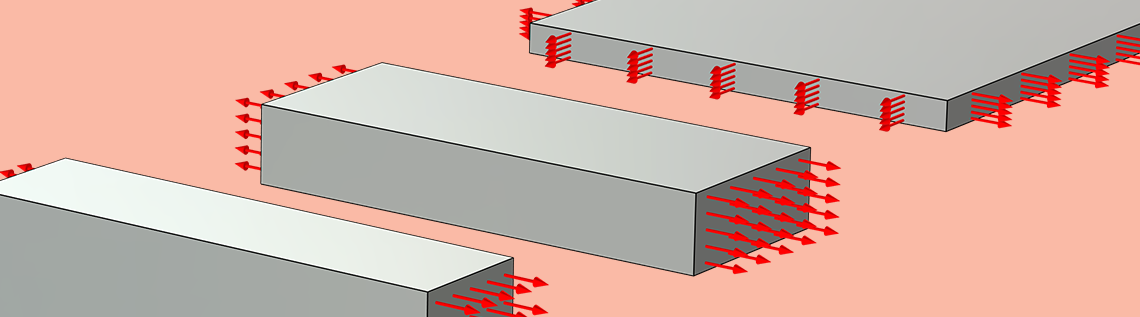
从左到右:橡胶薄板的单轴拉伸、纯剪切和等轴膨胀试验。红色箭头表示指定位移,在拉伸试验中表示施加的拉伸压力。
对于长宽比合适的试样,上述配置会在试样中心产生均匀的应力和应变状态。这些应力和应变可以通过可测量的量来估计,例如施加的位移和反作用力,或施加的压力和充气膜的曲率半径等。产生均匀的应力和应变状态的材料测试尤其适合进行参数估计,因为它们可以用单个单元建模,从而大大降低了计算成本。
从左到右:等效均匀单轴拉伸、纯剪切和等双轴拉伸的载荷情况。
非线性最小二乘参数估计
在获得实验数据并选择好材料模型后,我们还需要选择一种优化算法,将当前的模型预测与实验数据进行比较,并更新材料参数,使差值最小。因此,寻找未知材料参数 \mathbf{q}^* 相当于求解一个逆问题。我们用数学形式将其表示为一个加权最小二乘问题,
式中,\mathbf{W} 是权重矩阵,\mathbf{r} 是缺陷 或残余矢量,包含模型预测值 \mathbf{y} 与实验数据 \hat{\mathbf{y}} 之间的差值。模型预测可能明确或隐含地取决于材料参数,即 \mathbf{y} = \mathbf{y}(\mathbf{u}(\mathbf{q}), \mathbf{q}),\mathbf{u} 是正演问题的解。
为了更好地说明最小二乘问题的不同组成部分,可以将二次形式展开为
式中, N 是数据集的数量;Q_n 和 M_n 分别表示数据集 n 的最小二乘误差和数据点数量;P_n(\mathbf{q}; \lambda_m) 和 \hat{P}_{n,m} 分别表示模型预测值和实验数据。参数 \lambda_m 表示实验的自变量,如时间或施加的拉伸。此外,我们假设 \mathbf{W} 是一个对角矩阵,其分量为 1/s_{n,m}^2 ,其中 s_{n,m} 是比例因子,用于加权不同的数据点和数据集,并确保目标是无量纲的。最小二乘问题还可以通过参数的下限和上限进行扩展,用于排除参数空间中材料模型不稳定的非物理区域。
在 COMSOL Multiphysics® 中,有多种优化算法可用于求解最小二乘问题。大多数情况下,目标是参数的良好函数,使用基于梯度的 Levenberg–Marquardt 算法可以高效地求解这个问题。简单来说,Levenberg–Marquardt 算法通过在远离最小值时交替使用梯度下降方向的更新步长,以及在接近最小值时交替使用 Gauss–Newton 步长来迭代更新参数,从而实现近似二次收敛。更新算法中的一个基本量是雅可比因子
被用来衡量模型预测对材料参数变化的敏感度。原则上,可以在优化求解器中对雅可比进行分析估计;但是,如果问题高度非线性,且正演模型估计成本较低,则雅可比的有限差分近似通常在稳健性和效率方面更为可取。当无法正确计算雅可比时 —例如,如果目标是无差别的 — 无梯度二次近似约束优化算法(BOBYQA)是一种无需显式计算导数的替代算法。
还可以选择用 COMSOL Multiphysics® 中的 Levenberg–Marquardt 求解器计算置信区间以及协方差矩阵,作为参数估计不确定性的度量。如果您希望将实验数据中的方差传播到材料参数中,这将特别有用。要了解更多信息,请参阅通过协方差分析进行参数估计教学模型。
非线性材料参数估计示例
在上一篇博客中,我们探讨了如何利用两种常见载荷情况下应力-应变曲线的解析表达式来估计超弹性模型的材料参数。然而,这种方法无法轻松扩展到非弹性材料模型,因为非弹性材料模型通常不存在封闭解析解。作为替代,我们可以利用 COMSOL Multiphysics® 中的内置材料模型。对于两种载荷情况:超弹性和大应变黏弹性,我们将演示如何使用这种方法进行参数估计。
超弹性 Ogden 模型的参数估计
在第一个示例中,我们将根据代表软质弹性体的单轴拉伸、纯剪切和等双轴拉伸数据校准超弹性 Ogden 模型。数据如下。
代表软质弹性体的单轴拉伸、纯剪切和等轴拉伸数据。请注意,由于等轴应力比其他量大得多,因此绘制在第二个 y 轴上。
假设弹性体是不可压缩的,因此 Ogden 模型中的应变能密度为
这里考虑了应变能量密度函数中的两个项,因此问题包括求解 4 个未知材料参数 \mathbf{q} = (\mu_1, \alpha_1, \mu_2, \alpha_2),如下图所示。
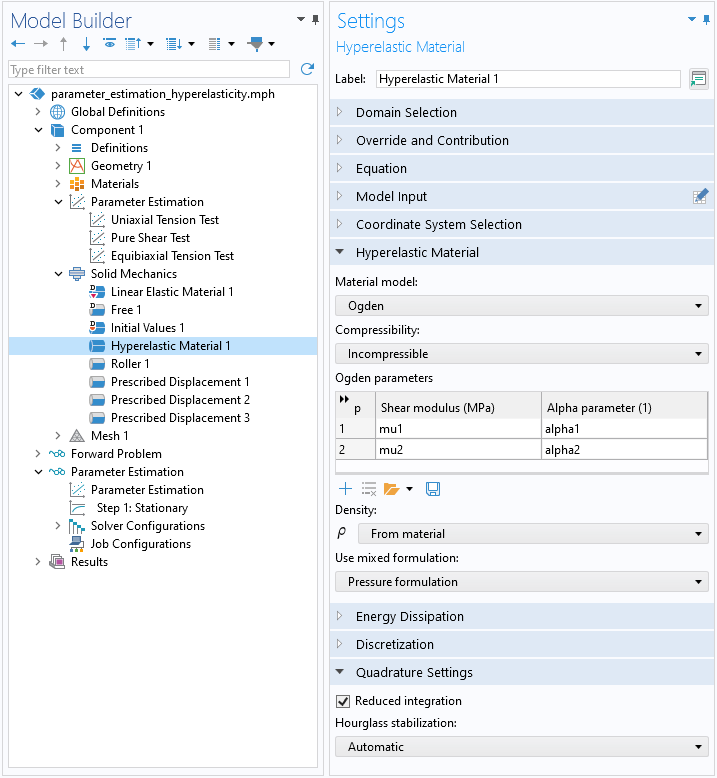
不可压缩 Ogden 模型的两个项的设置。请注意,由于载荷是均匀的,因此可以使用减缩积分来降低计算成本。
设置好材料模型后,可以将数据集导入结果表,并使用全局最小二乘目标 功能将数据集与相应的模型表达式连接起来。下图显示了根据单轴数据形成的最小二乘目标的设置。模型表达式 栏中使用的变量 comp1.P_ua 被定义为标称应力 solid.PxX 内置变量的体积平均值。
与单轴拉力数据相关的 全局最小二乘目标功能设置。
在参数估计 研究步骤中,我们添加了三个目标,并指定了要估计的材料参数。在估计参数 表中,mu1 和 alpha1 被限定为正值,而 mu2 和 alpha2 被限定为负值。这些限定确保了材料模型满足 Ogden 模型的已知稳定性要求 \mu_p\alpha_p > 0。
参数估计研究步骤的设置。
在优化求解器的每一次迭代中,都可以通过比较当前模型预测结果与实验数据的曲线图来监控求解进度。从下面的动画中可以看到,Levenberg–Marquardt 算法迅速改进了单轴和纯剪切模型的预测结果,并在多次迭代后改进了高度非线性的等轴响应。
黏塑性 Bergstrom–Boyce 模型的参数估计
在下一个示例中,我们将考虑更复杂的 Bergstrom–Boyce 黏塑性聚合物材料模型,它同时表现出应变率、载荷历史和温度相关性行为。以下是室温下两种不同应变率的循环单轴拉伸和压缩试验的代表性应力–应变曲线。
在两种不同应变率(0.1%/s和 10%/s)条件下,黏塑性聚合物材料模型典型的单轴拉伸和压缩加载–卸载曲线。
COMSOL Multiphysics® 6.2 版本超弹性材料 功能中的聚合物黏塑性 子节点包含 Bergstrom–Boyce 材料模型。在这里,父超弹性模型定义了一个弹性平衡网络,而子节点添加了一个平行的非平衡网络,其中包含一个弹性和非弹性单元。在本例中,我们使用几乎不可压缩的 Arruda–Boyce 应变能密度对弹性单元进行建模,并在黏塑性流动中包含应变和应力硬化。此材料模型总共包含 6 个独立的材料参数,\mathbf{q} = (\mu_0^\textrm{eq}, N_\textrm{c}, \beta_\textrm{v}, A, c, n):平衡网络的剪切模量,\mu_0^\textrm{eq};链段数量,N_\textrm{c};非平衡与平衡网络之间的能量系数,\beta_\textrm{v};黏塑性流动速率系数,A;应变硬化指数,c;应力硬化指数,n。
聚合物黏弹性功能中 Bergstrom–Boyce 模型的设置。图形窗口显示了单轴压缩和拉伸试验的单元模型。
现在,我们可以用类似于超弹性问题的方法来设置和求解最小二乘问题。从下面的动画中可以看到,尽管优化求解器需要进行约 12 次迭代才能达到收敛,但经过约 5 次迭代后,就已经得到了直观上令人满意的解。这是因为 Levenberg–Marquardt 求解器的默认终止条件是检查参数增量或缺陷矢量与雅可布角之间的最大角度是否小于给定的优化容差。在优化求解器的设置中,可以根据缺陷矢量的相对变化,选择加入一个额外的终止准则,如果求解器在参数空间中达到一个相对平滑的局部最小值,而目标函数的改进很小,那么这个终止准则就会非常有用。不过,默认的终止标准通常比基于缺陷减少的终止标准更稳健。
测试材料模型的稳定性
在估计出非线性材料模型的参数后,最好对材料模型进行测试,以确保其数值稳定性。在此系列博客的第二部分,我们将详细介绍这一主题。
结论及进阶学习
在这篇博客中,我们演示了如何在 COMSOL Multiphysics® 中根据典型材料测试数据估计非线性结构材料模型的参数。所介绍的方法通常适合任何类型的材料模型和材料测试数据。
要查看详细的分步说明,尝试自己对不同的模型进行参数估计,请参阅下列 COMSOL 案例库模型:



评论 (0)