如何在 COMSOL Multiphysics® 中模拟鼓泡现象

鼓泡是气体与液体之间的一种质量传递过程，常见于各种工业应用中，比如饮料碳酸化作用和光生物反应器，甚至在家中鱼缸中的充气，都属于这种现象。在这篇博客中，我们将详细介绍如何使用 COMSOL Multiphysics^® 软件对碳酸化作用这种鼓泡现象进行模拟。

什么是鼓泡？

鼓泡 是将气体吹进液体中产生气泡，从而将气体溶解在液体中或将液体从一些溶解的成分中剥离出来的过程。如上所述，此过程承载着气体到液体或液体到气体的质量传递。脱氧过程就是一个鼓泡的例子，在此过程中，氮气气泡穿过液体，排出或去除氧气和其他溶解气体。另一个例子是溶解，即气体溶解在液体中。溶解的物质可进一步与液体中的其他成分发生反应，改变液体的化学成分。碳酸化作用和充气是这类鼓泡/溶解现象的常见示例。

一瓶汽水的碳酸化作用产生的气泡。

当打开一瓶苏打水、汽水或其他任何碳酸饮料时，由于压力释放和浮力导致二氧化碳气泡上升，我们会听到“嘶嘶”的声音。然而，在打开瓶盖之前，二氧化碳是溶解在饮料（CO₂ (aq)）中的。这种溶解通过使二氧化碳气泡（通常在过饱和高压下）穿过饮料来实现。当二氧化碳气泡穿过饮料时，气体通过气泡表面向液体传递质量，溶解的二氧化碳与水发生反应生成碳酸，整个过程称为 碳酸化作用。

本文，我们将研究如何通过二氧化碳在水中的溶解来模拟碳酸化过程，也可以理解为，我们将制作虚拟碳酸水。

近距离观察碳酸化作用

如下图所示，从一杯水的底部引入二氧化碳。由于浮力作用，二氧化碳气泡上升并在水中穿行，传递质量和动量，最后通过顶面排出。请注意，溶解的二氧化碳与水反应生成碳酸。因此，为了模拟和理解玻璃杯中的碳酸化作用，我们需要求解以下问题：

• 水和二氧化碳气泡的质量和动量传递，即多相流
• 二氧化碳从气泡到液体的质量传递，即溶解
• 溶解的二氧化碳的质量传递以及后续发生的任何反应（如碳酸的生成）

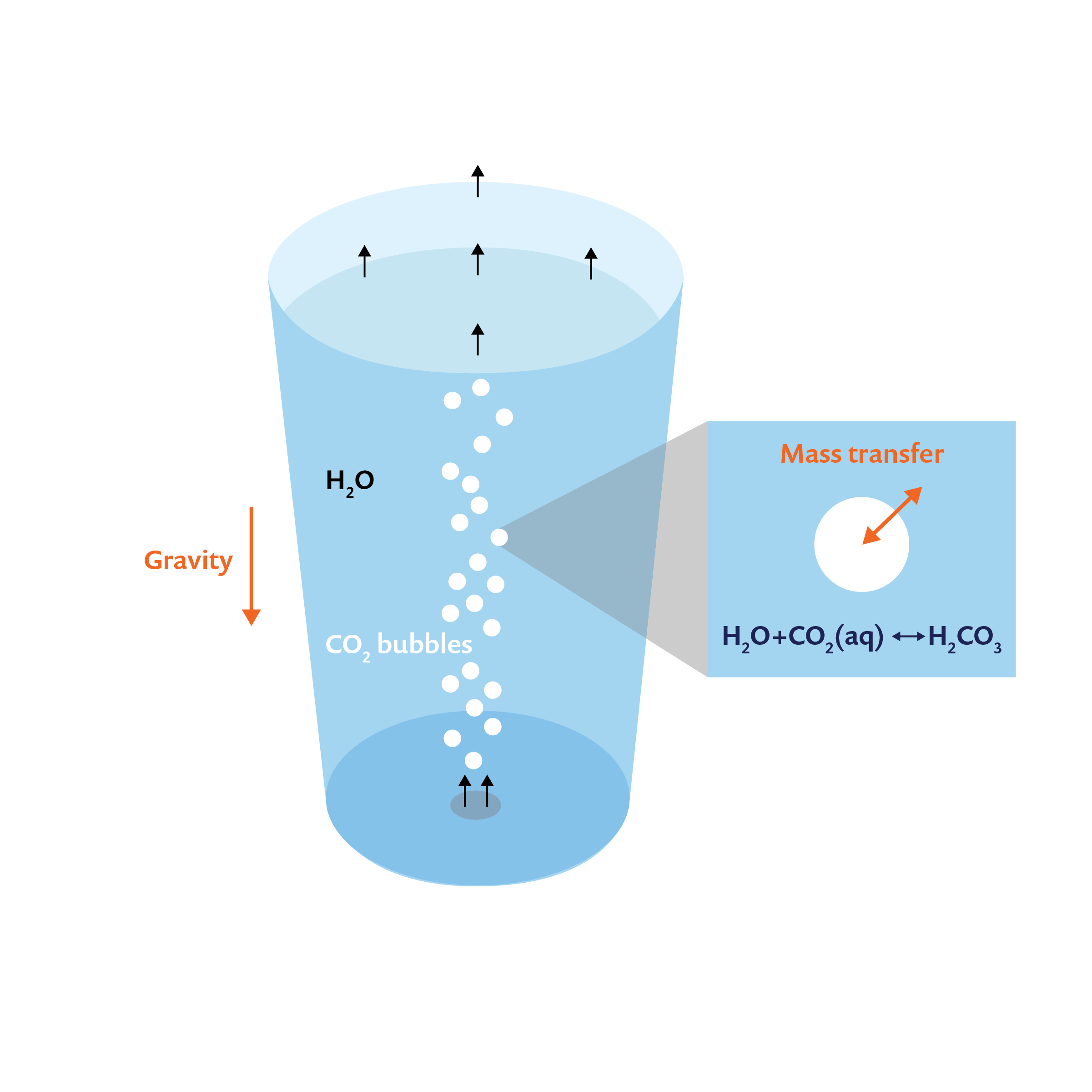
一杯水中的碳酸化作用示意图，二氧化碳气泡从底部进入。

在 COMSOL Multiphysics® 中模拟鼓泡

我们来看看在 COMSOL Multiphysics 中求解上述鼓泡问题需要用到的接口和条件。如上图所示，这个问题是轴对称问题。因此，我们可以使用二维轴对称组件来构建模型。由于气泡的容积率小于 1%，二氧化碳气体的密度与水相比可以忽略不计，我们使用 气泡流，层流 接口模拟多相流。当气泡的容积率小于 1% 时，也可以使用粒子追踪来求解气泡的输送。但请注意，气泡流可用于模拟气泡容积率大于1%（约为 10% 或更小）的系统。

此外，由于根据气泡速度计算的雷诺数低于内部流动的雷诺数 2000，因此我们选择层流。

提示：您可以通过阅读 COMSOL® 软件中关于不同类型多相流接口的博客，了解它们的优缺点以及相应的基本假设。

气泡流，层流 接口不仅可以求解速度、压力和有效气体密度，还可以计算气泡的数密度和相关的界面面积（在设置中选择 求解相界面面积 选项时）。因此，我们能够使用双层膜理论来计算气泡与液体之间的质量传递，这个问题将在后文进行讨论。

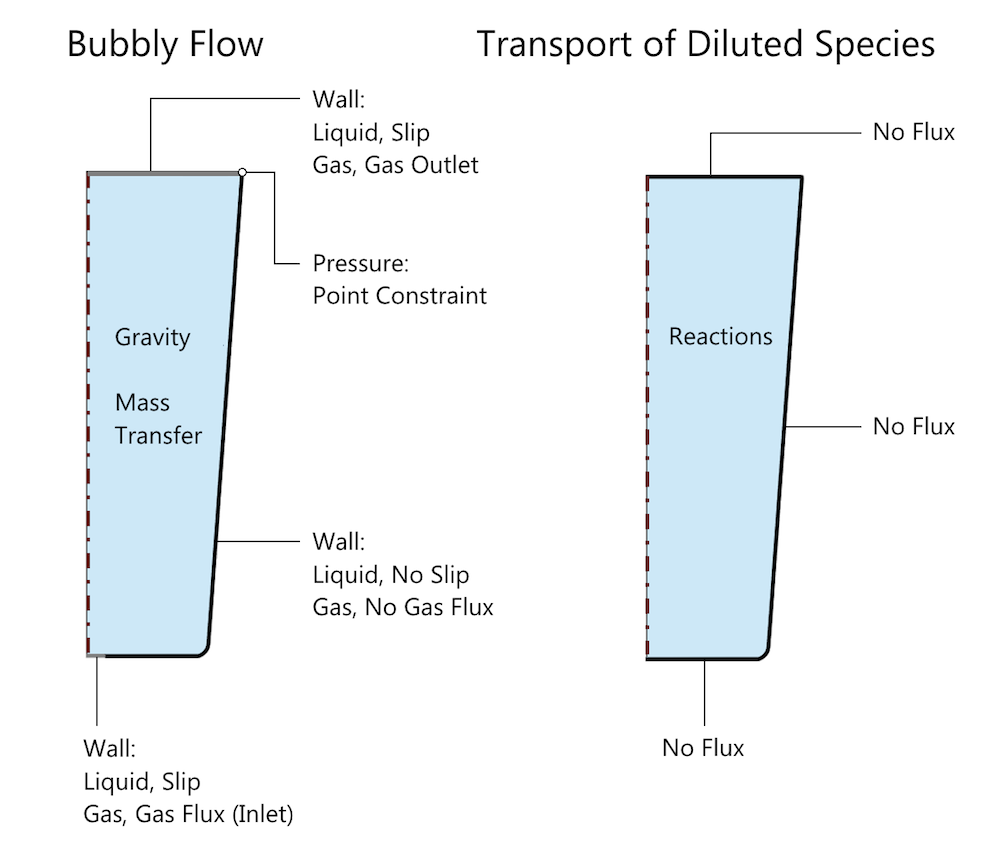
COMSOL Multiphysic 中的问题设置示意图，显示了 气泡流 和 稀物质传递 接口相关的边界和域条件。二氧化碳的质量传递通过 反应 条件来指定，碳酸反应通过 平衡反应 条件来指定，二者都由该示意图中的 反应 表示。注：没有指出默认域条件，如 流体属性、传递属性 和 初始值 。

请注意，模拟流体流动时，我们假设自由表面（即水面）的变形可以忽略不计。不过，由于这是一个自由表面，因此在边界处选择了 滑移壁条件，如上图所示。这一条件支持水作切向运动，但将法向速度限制为零。气体入口和出口条件在该接口的 壁 边界条件下指定。（您可以在之前 关于模拟啤酒中的气泡流的博客中找到关于这一过程的更多详细信息。）为了保持一致性，入口气体通量从零增加到所需的值，这是一种载荷随时间变化的方法，是一种不错的实践方法。

二氧化碳和水的平衡反应所产生的含水二氧化碳和碳酸的传递通过 稀物质传递 接 口模拟，该接口求解了含水二氧化碳和碳酸的浓度。请注意，本例中我们只考虑生成碳酸的反应。气泡流（bf）和 稀物质传递（tds）的相关边界条件如上图所示。

二氧化碳从气泡到液体的质量传递通过 气泡流 接口的 质量传递 条件来建模。本例中，我们使用 双层膜理论 选项，该选项利用亨利定律 来计算从气体到液体所需的质量传递m_{gl} ，由下式给出：

其中：

• k 是必须指定的质量传递系数，取自实验或文献资料
• c 是溶质的浓度；在本例中，为含水二氧化碳的浓度 c_CO2，通过稀物质传递 接口计算
• M是气体（二氧化碳）的分子量
• a 是通过气泡流 接口计算的单位体积界面面积
• {c^*}是根据亨利定律（c^* = (p+p_
  {ref})/H）计算的平衡浓度，其中：
  • p是根据气泡流 接口计算的相对压力
  • p_{ref} 是在气泡流 接口中指定的参考压力
  • H是亨利常数，取自实验或文献资料

从气体到液体的质量传递是含水二氧化碳的来源，通过 稀物质传递 接口中的 反应 项进行分析，如下所示。除了 稀物质传递 与 气泡流 接口之间的耦合外，通过 气泡流 接口计算的液相速度在 稀物质传递 接口的 传递属性 域设置下传递，这解释了含水二氧化碳的对流传递。

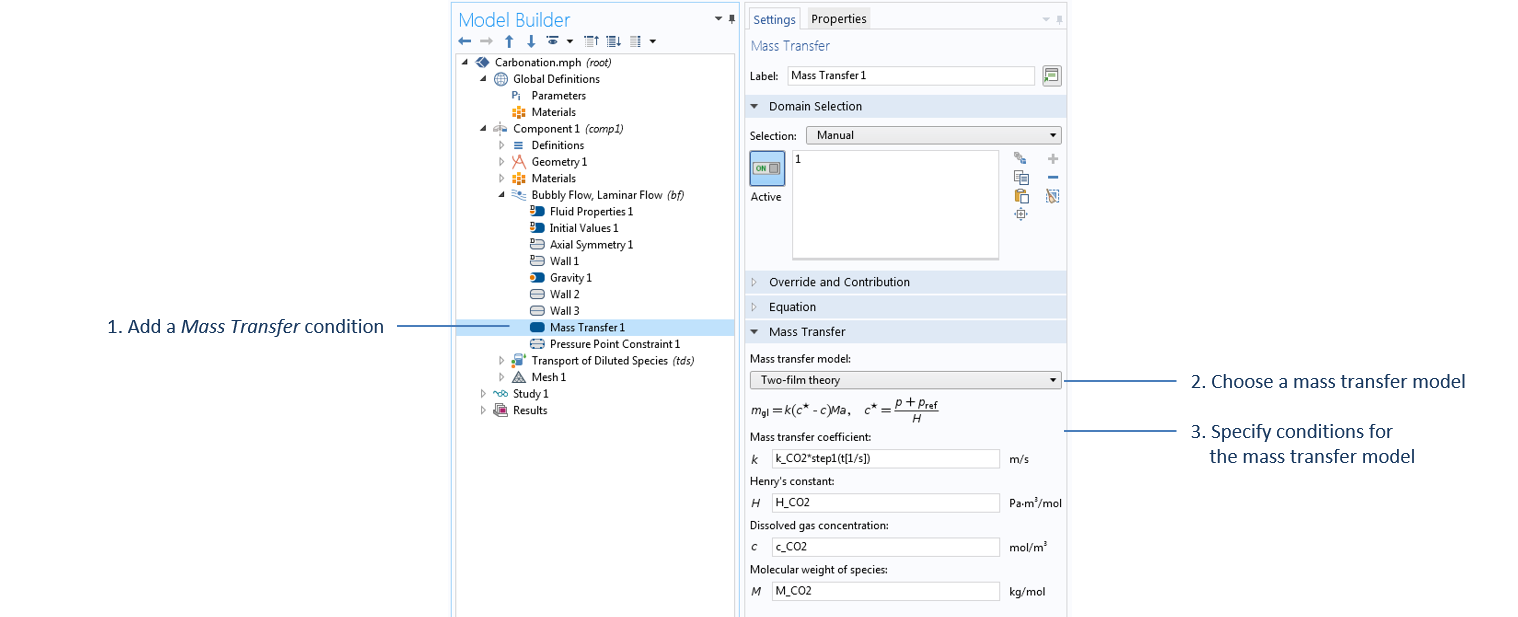
气泡流接口中 质量传递 条件的设置。该域特征中的所有参数都在 参数节点下定义，但 c_CO2 除外，它是在 稀物质传递接 口中计算的二氧化碳浓度。

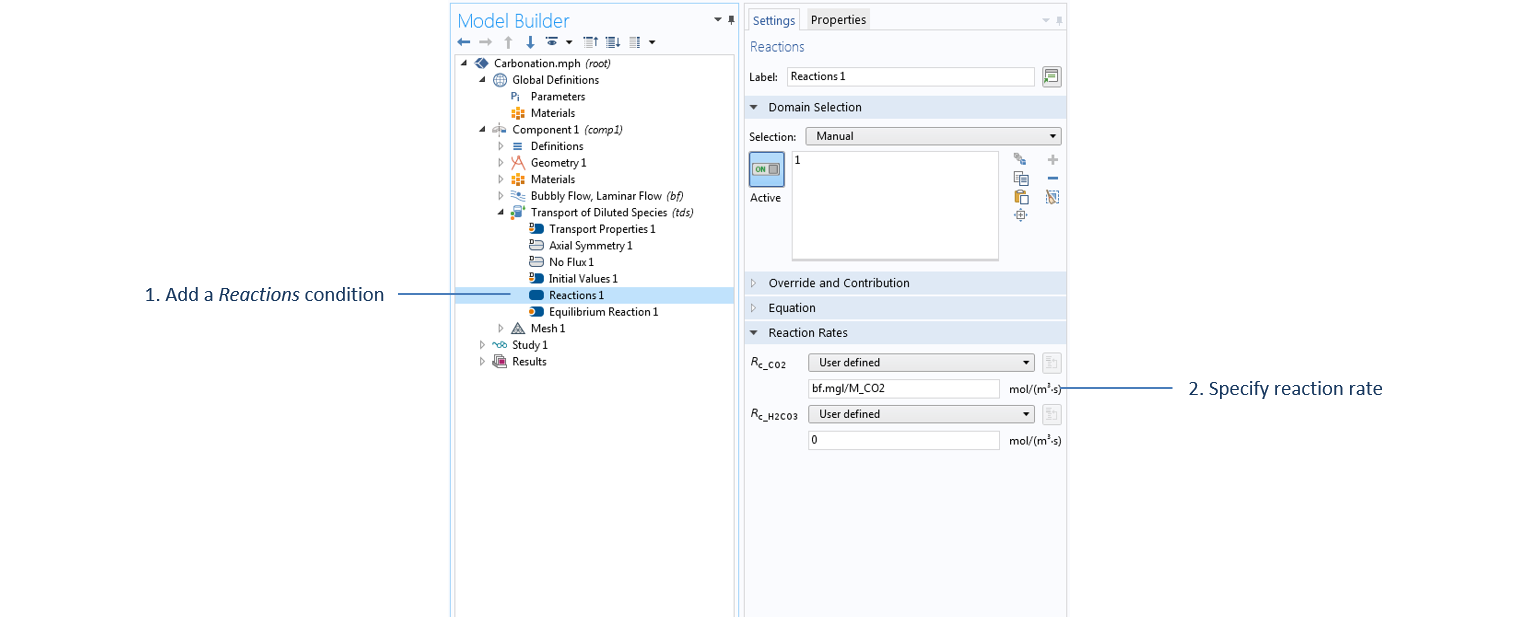
稀物质传递 接口中 反应 项的设置，其中质量传递值 bf.mgl 在 气泡流 接口中计算，并在 稀物质传递 接口中作为源/汇项传递。

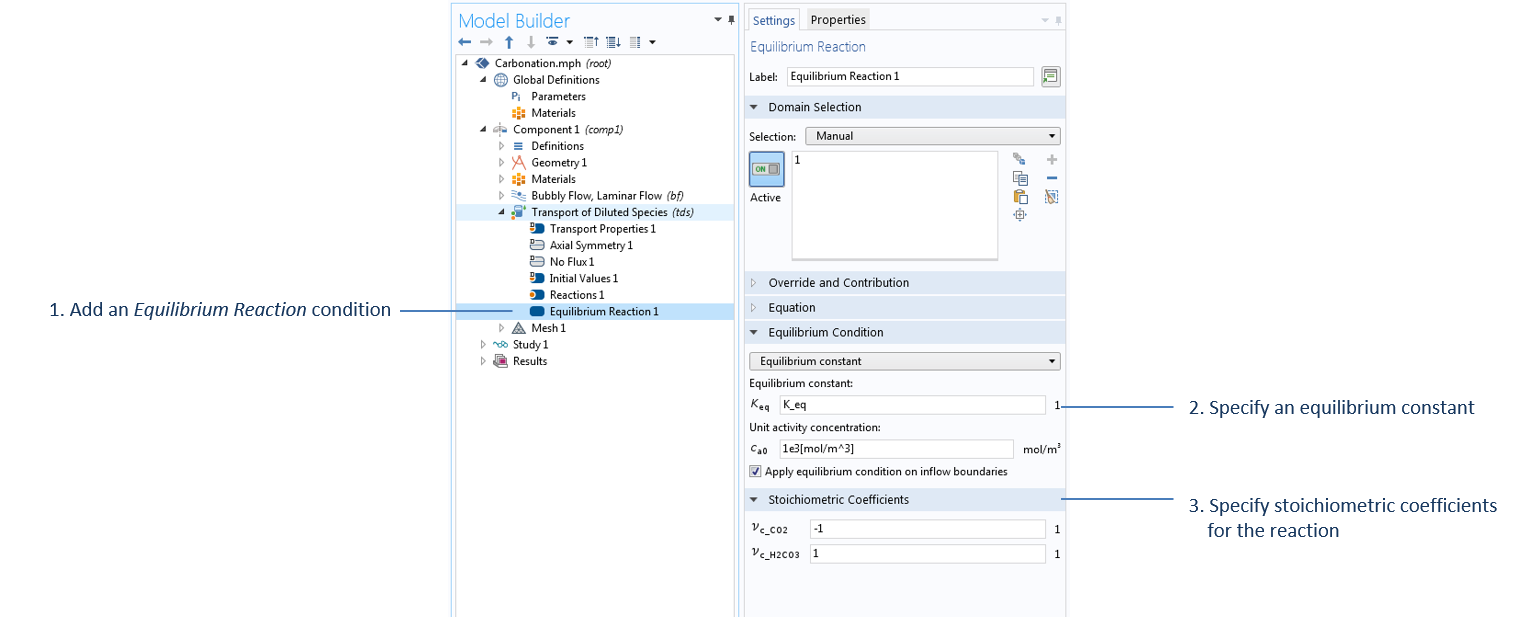
用于指定平衡反应 H₂O + CO₂ (aq) ↔ H₂CO₃ 的设置，水在 稀物质传递 接口中用作溶剂，其中 K_eq 在 参数节点中定义。

鼓泡过程的仿真结果

二氧化碳的质量传递和含水二氧化碳扩散的相关输入信息取自文献资料（参考文献 1-3）。

通过比较下图中 t = 0 s 和 t = 10 s 时的绘图，可以明显看出二氧化碳气泡（通过气体体积分数来量化）开始在水中上升，并赋予水动量，最后通过顶面排出。然而，由于水不通过顶面流出，它开始在玻璃杯中循环，导致产生下图中观察到的涡流。质量传递发生在气体体积分数非零的区域，因此，最初含水二氧化碳的浓度与气体体积分数紧密相关。然而，含水二氧化碳通过对流和扩散传递到玻璃杯的其余部分，当你比较下面的速度（包括流线）和含水二氧化碳浓度表面图时，可以看到对流传递占主导地位。

t = {0, 10, 50, 100} s 时，水的速度大小以及流线（左）、二氧化碳气泡体积分数（中）和含水二氧化碳浓度（右）。

在 COMSOL Multiphysics 中，我们还可以创建并导出上述绘图的动画，这有助于更好地观察旋涡的形成、随时间的演变以及稀物质的传递。

水的速度大小随流线（左）、二氧化碳气泡体积分数（中）和含水二氧化碳浓度（右）的演变过程。

由于这是二维轴对称仿真，COMSOL Multiphysics 软件会自动创建三维数据集，这是计算研究中二维数据集的一次变革。因此，我们可以创建一个碳酸随时间演变的三维动画，其中碳酸的生成和传递与含水二氧化碳的传递紧密相关。

碳酸浓度随时间的演变。

结束语

在这篇博客中，我们通过水的碳酸化作用示例讨论了如何模拟鼓泡现象。一般来说，类似的过程可用于模拟分散多相流中任意两种流体之间的质量传递，请注意，在气泡流 和 混合物模型 接口中均包括 质量传递 条件。你还可以在 质量传递条件下通过向下滚动 质量传递 模型下的列表来指定用户定义的表达式。

模拟这类多物理场问题时，从简单的模型开始，然后再逐渐增加模型的复杂度是 最优的建模工作流程。

后续操作

你是否对气泡建模非常感兴趣呢？单击下面的按钮，下载碳酸化作用案例模型。请注意，你必须有 COMSOL Access 帐户和有效的软件许可证才能下载相关的 MPH 文件。

有关离散和分散多相流建模的更多信息，请查看以下案例模型：

• 气升式环流反应器中的流动
• 喷墨打印机
• 使用水平集、相场和动网格的自由表面建模：比较

参考文献

1. Sander, R., Compilation of Henry’s law constants for inorganic and organic species of potential importance in environmental chemistry, Air Chemistry Dept., Max-Planck Inst. of Chemistry, 1999.
2. Hogendoorn, J.A., Bhat, R.V., and Versteeg, G.F., “On the Determination of the Diffusivity of CO 2 in Aqueous and NonAqueous Solvents: Investigations with Laminar Jets and Wetted Wall Columns”, Chemical Engineering Communications, vol. 189, no. 8, pp. 1009–1037, 2002.
3. Han, J., Eimer, D.A., and Melaaen, M.C., “Liquid phase mass transfer coefficient of carbon dioxide absorption by water droplet”, Energy Procedia, vol. 37, pp. 1728–1735, 2013.