Menu
COMSOL 博客

图像去噪以及其他多维变分问题

Author Image
作者 Temesgen Kindo
2018年 9月 21日

我们之前讨论了如何用 COMSOL Multiphysics 软件解决一维变分问题，并使用统一的强制约束（第3部分: 强制约束中数值问题的处理方法）框架实现复杂的域和边界条件。今天，我们使用了一个有意思的例子：变分图像去噪，将问题的讨论扩展到多维度、高阶导数和多个未知数。文章最后，我们对这个变分问题相关的系列博客进行总结，并对进一步的研究提出了一些建议。

高维空间中的变分问题

（之前的讨论中）考虑的是一维问题，并寻找一个函数 u_(x) 使函数最小化

E[u(x)] = \int_a^b F(x,u,u^{\prime})dx.

 
现在，让我们考虑更高维的空间，同时只考虑一阶导数。考虑使下式最小化的变分问题

E[u(x,y,z)] = \int_{\Omega}F(x,y,z,u,u_x,u_y,u_z)d\Omega,

 
定义在固定域 \Omega. 上

相邻函数 u+\epsilon\hat{u} 就变成

E[u+\epsilon\hat{u}] = \int_{\Omega}
F\left(x,y,u+\epsilon\hat{u},\frac{\partial}{\partial x}(u+\epsilon\hat{u}
),\frac{\partial }{\partial y}(u+\epsilon\hat{u}),\frac{partial } {\partial z}(u+\epsilon\hat{u})\right)d\Omega.

 
与一维问题一样，一阶最优必要条件为

\frac{d}{d\epsilon}\bigg|_{\epsilon=0}E[u+\epsilon \hat u] = 0,

 
这意味着

\int_{\Omega} \left[\frac{\partial F}{\partial u}\hat{u}
+\frac{\partial F}{\partial u_x}\hat{u}_x+\frac{partial F} {\partial u_y}\hat{u}_y+\frac{\partial F}{\partial u_z}\hat{u}_z\right]d\Omega = 0, \quad \forall \quad \hat{u}(x,y,z).

 
为了得到变分导数，我们构建了一个函数，其本质是标量参数的函数 \epsilon 并使用单变量演算方法。对于固定域，一种更快的正式方法是用变分导数符号表示为：

\delta E = \int_{\Omega} \delta Fd\Omega=\int_{\Omega} \left[\frac{\partial F}{\partial u}\delta u + \frac{\partial F}{\partial u_x}\delta u_x + \frac{\partial F}{\partial u_y}\delta u_y + \frac{\partial F}{\partial u_z}\delta u_z\right]d\Omega

 
这里，\delta u 对应于之前使用的符号 \hat{u}。注意，由于域是固定的，因此我们仅考虑函数及其导数的变化。如果域可以随解而变化，那么变分导数将包含来自边界变化的额外贡献。

图像去噪：一个多维变分问题

近几十年来，变分方法为图像处理带来了强大而严谨的技术，例如去噪、去模糊、修复和分割。今天，我们就以降噪为例来说明。总变分最小化 是一种用于图像去噪的技术。假设我们有一个图像数据，已被噪声破坏。图像上有斑点（有时称为“脉冲噪声”）。我们想要尽可能多的恢复原始图像，所以图像必须被去噪。

含细节错误的图像会包含高变分；因此，去噪后的图像应具有尽可能小的变分。经 Tikhonov 处理的模型将这个总变分测量为

TV(u) = \int_{\Omega}|\nabla u|^2d\Omega = \int_{\Omega}\nabla u \cdot \nabla ud\Omega.

 
仅将总变分最小化会尽可能地平滑数据并返回接近常数的解，从而丢失图像中的合理细节。为了防止出现这个问题，我们还希望将输入数据与解之间的差异最小化，由保真项给出

f(u)=\int_{\Omega}(u-u_o)^2d\Omega.

 
现在，我们有了多个可能相互冲突的目标，我们尝试通过引入新函数来折中

E(u) = \int_{\Omega}\left[ \nabla u \cdot \nabla u + \mu (u-u_o)^2\right]d\Omega

 
其中，正则化参数确定强调细节还是去噪（这是由用户指定的正数）。

如上一节所述，我们现在准备导出一阶最优条件。需要一个消失的变分导数，我们得到

\delta E = \int_{\Omega}\left[2 \nabla u \cdot \delta (\nabla u) + 2\mu (u-u_o)\delta u\right]d\Omega = 0 , \quad \forall \quad \delta u.

 
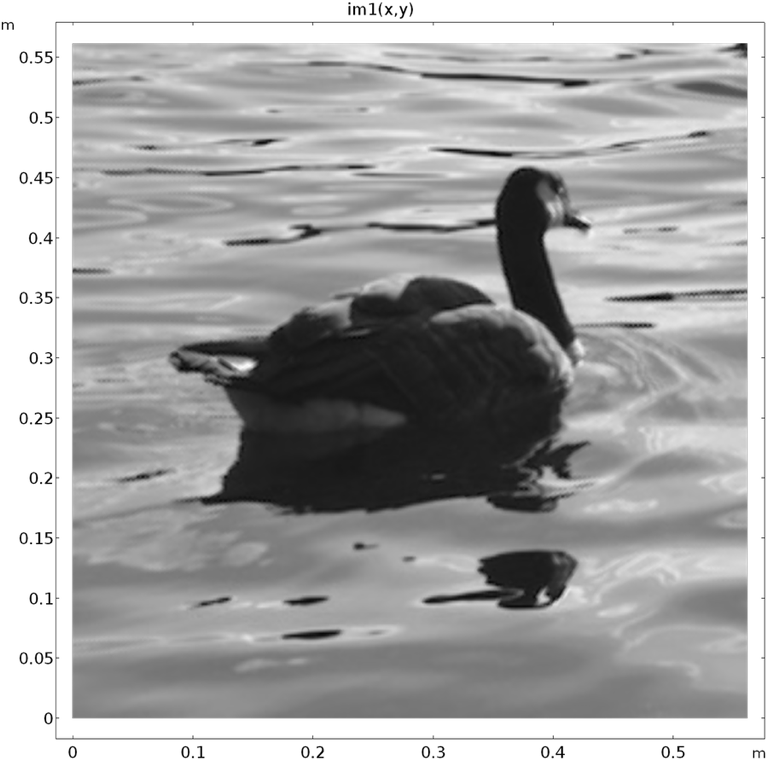
为了演示这个过程，我们将图像导入 COMSOL Multiphysics，并添加随机噪声来破坏它。以下是破坏了我同事提供的一只鹅的图像后得到的结果：

鹅的图像由于随机噪声而损坏
被随机噪声故意破坏的测试图像。

上面的弱形式以矢量表示法给出。为了在计算中使用，我们将其写为笛卡尔坐标表示，并忽略公因数 2。

\int_{\Omega}\left[u_x\hat{u}_x + u_y\hat{u}_y + \mu (u-u_o)\hat{u}\right]d\Omega = 0 , \quad \forall \quad \hat{u}.

 
将此公式输入到 COMSOL® 软件中，如下面的屏幕截图所示。通过在所有边界上使用 Dirichlet 边界条件 u=uo，保留边上的数据，并使用正则化参数 1e6。在较简单的算法中，正则化参数是通过试错法确定的。如果生成的图像缺少相关细节，则我们增大参数；如果认为结果太嘈杂，我们就减小参数。

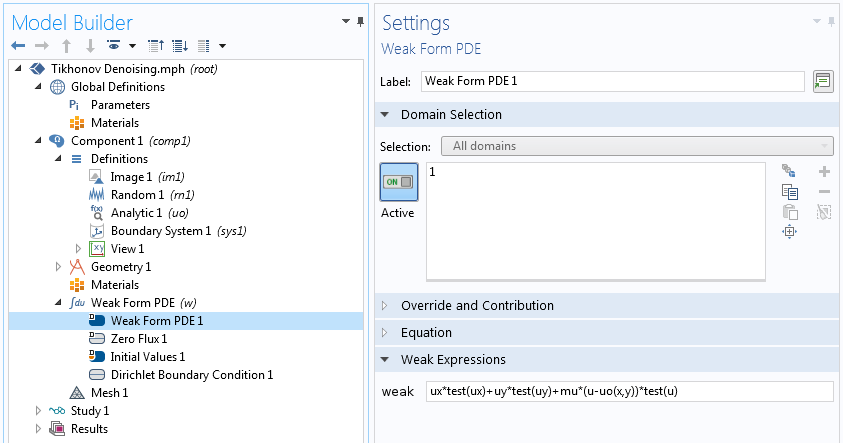
屏幕截图显示了如何在 COMSOL Multiphysics 中指定 2D 中的变化问题。
在二维中指定变分问题。

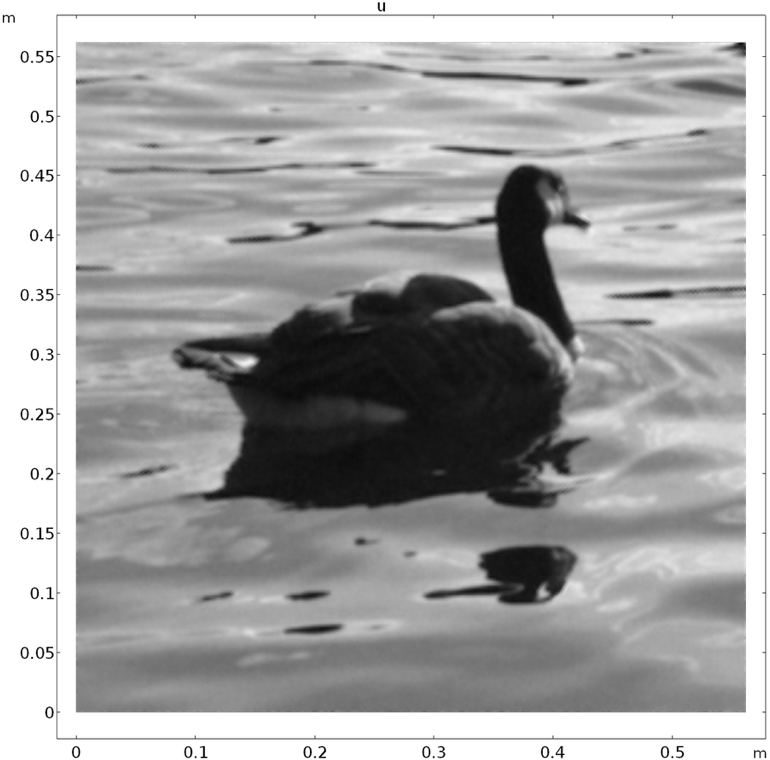
下面是去噪后的图像，以及原始图像——对于基本模型来说还不错！

鹅的去噪的图像
图像降噪之前的原始鹅照片

去噪图像（左）和原始图像（右）。

Tikhonov 正则化会过于平滑，并且不会保留诸如边和角之类的几何特征。由下式给出的 ROF 模型的函数

E(u) = \int_{\Omega}\left[ |\nabla u| + \mu (u-u_o)^2\right]d\Omega

 
在这方面做得更好。

到目前为止，通过将变分导数设置为零而获得的最优性的一阶必要条件是

\delta E = \int_{\Omega}\left[ \frac{\nabla u}{|\nabla u|}\cdot \delta (\nabla u) + 2\mu (u-u_o)\delta u\right]d\Omega = 0 \quad \forall \delta u.

 
请注意，在函数中使用绝对值会导致高度非线性的问题。另外，分母 |\nabla u| 可能在数值迭代中变为零，从而产生除零错误。为了防止这种情况，我们可以给它添加一个小正数。在 COMSOL Multiphysics 中，我们经常使用浮点相对精度 eps，大约是 2.2204 \times 10^{-16}。

ROF 模型保留了边缘，但据说会引起所谓的“阶梯效应”。在函数中包含高阶导数有助于避免这种情况。

高阶导数的变分问题

下面，我们讨论高保真图像处理和其他涉及高阶导数的变分问题。这方面的一个传统课题是弹性梁和板的分析。例如，在欧拉梁理论中，一个具有杨氏模量 E 和截面惯性矩 I 的梁，施加横向载荷 f 使其弯曲以最小化总势能

\int\left[\frac{1}{2}EI(\frac{d^2u}{dx^2})^2-fu\right]dx.

 
对于较小的变形，分析忽略了域的变化，因此可用类似于下式的变分公式求解

\delta \int\left[\frac{1}{2}EI(\frac{d^2u}{dx^2})^2-fu\right]dx = \int\left[EI\frac{d^2u}{dx^2}\delta(\frac{d^2u}{dx^2})-f\delta u\right]dx = 0 \quad \forall \delta u .

 
请注意，我们没有对变分导数中的杨氏模量求微分，因为我们考虑的是线性弹性材料，其中材料属性与变形无关。对于非线性材料，必须包括材料属性对变分导数的贡献。该功能内置于 COMSOL Multiphysics 的附加产品——非线性结构材料模块中。

在函数中包含高阶导数不会给我们发现一阶最优性准则的方法带来任何概念上的改变，但是它确实具有计算上的含义。有限元插值函数中 在弱形式偏微分方程设置的离散化设置窗口 中，需要具有与变分形式中的最高阶空间导数相同或更高的多项式幂。例如，对于梁问题，存在变分形式的二阶导数，因此我们无法选择线性形状函数。如果我们这样做了，方程中的所有二阶导数都会一致消失。我们必须使用二次或更高阶的形状函数。

多未知数变分问题

到目前为止，我们已经考虑了最小化只基于一个未知数 u 的函数。通常，函数包含不止一个未知数。假设我们还有另一个未知数 v 和一个函数

E(u,v)=\int_{\Omega}F(x,y,z,u,v,u_x,u_y,u_z,\dotsc)d\Omega.

 
这个函数的第一个变分是

\delta E=\int_{\Omega}\left[\frac{partial F} {\partial u}
\delta u+\frac{\partial F}{\partial v}\delta v + \frac{partial F} {\partial u_x}\delta u_x+\frac{\partial F}{\partial u_y}\delta u_y+\frac{partial F} {\partial u_z}\delta u_z + \frac{\partial F}{\partial v_x}\delta v_x+\frac{partial F} {\partial v_y}\delta v_y+\frac{\partial F} {\partial v_z}\delta v_z+…\right]d\Omega.

 
这里，我们假设两个场 u 和 v 彼此独立，因此，我们可以对两个变量进行独立变分。有时，情况并非如此：变量之间可能存在约束。

变量之间最简单的约束是，当一个变量显式地以另一个变量的形式给出时，如 v = g(u)。在这种情况下，我们对于以下函数，可以选择消除 v

E(u,v)=\int_{\Omega}F(x,y,z,u,v,u_x,u_y,u_z,\dotsc)d\Omega.

通常，我们有以下形式的约束 g(u,v,\dotsc)=0，并且我们不能用代数的方法转换这个表达式。在这种情况下，我们使用系列博客第3部分中讨论的有关强制约束的技术。例如，对于拉格朗日乘数法，我们有一个由下式给出的增广函数

\mathcal{L}(u,v,\lambda) = \int_{\Omega}\left[F+\lambda g\right]d\Omega,

 
其中， \lambda = \lambda(x,y,z) 为分布式约束，或

\mathcal{L}(u,v,\lambda) = \int_{\Omega}Fd\Omega\quad +\quad \lambda g,

其中，\lambda 为全局约束的常数。

我们使用相同的 弱形式偏微分方程 接口来指定这类多场问题。问题是：我们是使用单个接口还是为每个未知函数都使用一个接口？这取决于未知函数之间的关系。一种情况，如果 u 和 v 是同一物理矢量的不同分量，例如位移或速度，我们可以使用相同的接口，并在因变量 部分指定因变量的数目。另一种情况，如果 u 代表温度，v 代表电势，我们可以使用不同的偏微分方程接口。如果我们出于某种令人信服的原因，必须对同一未知向量的不同分量使用不同的离散化或缩放，我们也可以使用多个接口。当我们有多个未知数时，我们必须仔细选择每个场的插值函数（如之前博客文章中有关多物理场模型中单元阶次中介绍的那样。）

结束语

变分方法提供了一个统一的框架对大量科学问题进行建模。COMSOL Multiphysics 中包含的弱形式偏微分方程接口，使我们能够引入自己的变分问题来扩展 COMSOL® 软件的功能。在这一系列博文中，我们通过解决一些问题来证明了这种功能，这些问题包括找到皂膜的形状，为湖边的徒步旅行者规划路线以及修复损坏的图像。

请记住，一些重要的偏微分方程并不是来自最小化泛函数。Navier-Stokes 方程是就是一个示例。我们仍可以在导出他们的弱形式后，使用弱形式偏微分方程 接口求解这类问题。

求解变分问题的一个重要部分是指定约束。本系列的前三篇博客文章讨论了强制约束的数学公式和数值分析。

这里需要注意的是，我们仅考虑了优化的必要条件。消除一阶导数不足以达到极小值。一阶导数在最大值上也消失了。在本系列讨论的示例中，我们考虑了众所周知的问题，在这些问题中通过解提供最小值。在处理新问题时，一定要在结束计算前检查二阶最优性准则以及最小值（最大值）的存在和唯一性。对于这个以及其他变分问题分析和数值方面的问题，我给大家提供一些我喜欢的参看文献，希望会对您有所帮助：

  • 关于变分演算的经典文献：
    • I.M. Gelfand and S.V. Fomin (English translation by R.A. Silverman), Calculus of Variations, Dover Publications, Inc., 1963.
  • 最近讨论工程问题的文章：
    • K.W. Cassel, Variational Methods with Applications in Science and Engineering, Cambridge University Press, 2013.
    • J.W. Brewer, Engineering Analysis in Applied Mechanics, Taylor & Francis, 2002.
  • 强制约束的策略：
    • D.G. Luenberger, Introduction to Linear and Nonlinear Programming, Addison-Wesley Publishing Company, 1973.
    • S.S. Rao, Engineering Optimization: Theory and Practice, John Wiley & Sons Inc., 2009.

希望本系列文章使您对使用 COMSOL Multiphysics 模拟变分问题有所了解，尤其当你需要建模的问题还未在软件中内置时。

祝您建模愉快，如有任何疑问，请通过下面的按钮与我们联系：

联系 COMSOL

查看更多关于“变分问题和约束”的系列博客文章

博客分类

相关主题

评论 (0)

正在加载...
浏览 COMSOL 博客
类别
标记