自然对流现象存在于电子设备冷却、室内气候系统和环境运输等众多科学与工程应用中。在 COMSOL Multiphysics® 5.2a 版本中,CFD 和传热模块新增的一些功能使建立自然对流模型及其求解变得更加简单。在这篇博客,我们将概述自然对流现象和相关的新功能,并讨论在模拟自然对流时可能遇到的一些问题。
什么是自然对流?
自然对流是一种由流体内部的浮力引起的传输,而这种浮力又是由温度或组分差异引起的流体密度变化产生的。
您可能对室内环境系统中的自然对流概念比较熟悉。在这种场景中,热空气上升到天花板,并靠近热源,冷空气则会下沉到地面并靠近较冷的表面,例如冬季的窗户。
电子设备冷却则是另一种依靠自然对流工作的过程。例如,我们不想使用有噪声的风扇为家庭影院系统的扬声器和电视机降温。电子设备需要在安静的工作环境下运行,它通常依靠内置散热器上方的自然使空气循环。
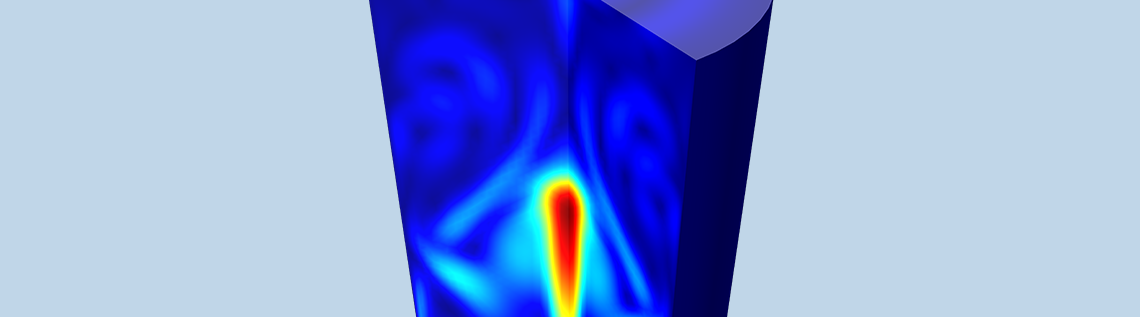
从底部加热的张开的钉柱翅片散热器周围的自由对流。动画显示了散热器周围空气的速度。
在化工和食品加工等行业,自然对流问题相对不明显。环境科学和气象学也存在自然对流问题,科学家和工程师需要尽可能准确地预测和理解空气和水中的传输现象。
对于上述所有案例,理解和设计控制自然对流系统对工程师和科学家而言至关重要。在这种情况下,数值仿真是一种有效的方法。COMSOL Multiphysics 新版本软件增加的许多新功能,使工程师和科学家可以更轻松地定义和求解涉及自然对流的问题。
流体流动接口的弱可压缩流动选项 忽略了对自然对流影响较小的压力波。在该选项下,您可以设置更大的时步,进而缩短求解自然对流问题的时间。
Boussinesq 近似 的 不可压缩流动 选项使用了一个热膨胀系数对浮力驱动的对流密度进行线性化处理。该选项仅将密度变化作为动量方程中的体积力。相较于 弱可压缩流动 选项,这进一步简化了模型,同时仍能准确且高效地描述密度变化较小的系统。对于温差较小的水体中的自由对流,这种简化几乎总是有效的。
重力功能不仅简化了定义静水压力的参考点的流程,还能自动考虑垂直边界处静水压力的变化。
接下来,我们将进一步了解这些新功能,并演示如何将其应用于自然对流仿真问题。
使用弱可压缩流动选项求解自然对流问题
非等温流动 接口包括 弱可压缩流动 选项。该选项通过忽略压力导致的密度变化简化流动问题。同时避免了对压力波的描述,解析压力波必须设置密集的网格和小时步,因此计算时间相对较长。在自然对流中,压力波的影响往往微乎其微,这意味着上述简化处理几乎不会影响模型的准确度。
可压缩流体的连续性方程如下:
(1)
其中 ρ 表示密度,u 表示速度矢量。
对于气体而言,密度与压强和温度相关。例如,对于理想气体,可以用下列公式表示:
(2)
如果忽略密度变化的动态压力效应,我们可以得到:
(3)
如果使用理想气体密度的表达公式,同时忽略动态压力对密度的影响,我们得到以下连续性方程:
(4)
这意味着,密度变化只与温度变化有关。密度变化可能导致流体的膨胀,但当使用了 弱可压缩流动 选项时,流体膨胀对压力场的直接动态效应可忽略不计。
除了使用连续性方程描述密度变化之外,还需要在流体流动接口的设置中勾选重力复选框,以在重力方向的动量方程中添加体积力。在默认设定下,重力方向为负 z 方向。因此,体积力的方程如下:
(5)
其中密度 ρ 是温度的函数。
对于理想气体,密度与温度成反比。
选择非等温流动 或 共轭传热 接口,即可以访问 弱可压缩流动 选项的设置窗口。在模型开发器选择 流体流动 接口节点后,便会出现设置窗口。然后,选择 弱可压缩流动 选项,消除压力和密度之间的相关性,同时启用重力选项,浮力的体积力将自动添加到动量方程中。
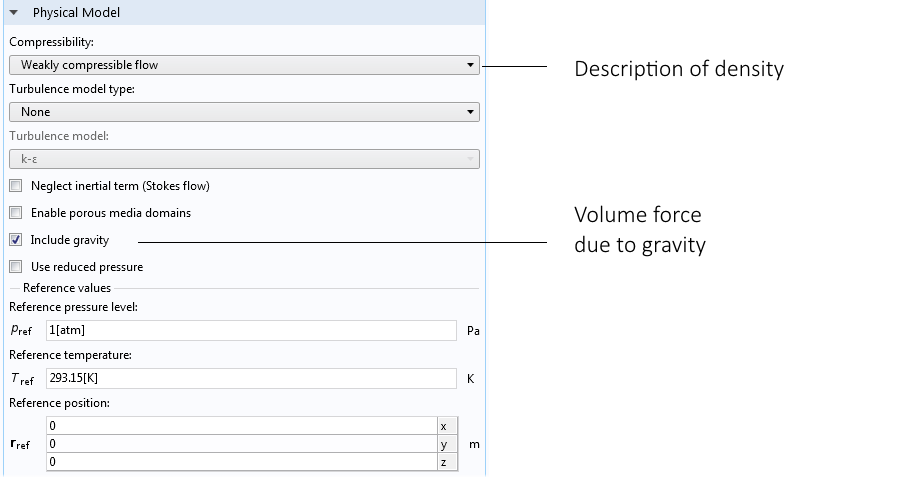
流体流动接口的设置窗口显示了 弱可压缩流动选项和重力功能。
下图显示了两个垂直放置的电路板之间的流动,图中仅显示了一块电路板单元。第二块电路板位于正前方,其背面面向第一块电路板。流动完全由浮力驱动;即没有风扇(自然对流)。
入口的流率为 0.2 m/s,出口处约为 0.3 m/s。侧面没有进气口,这意味着流速差是由沿电路板之间通道高度的温度升高引起的膨胀导致的。
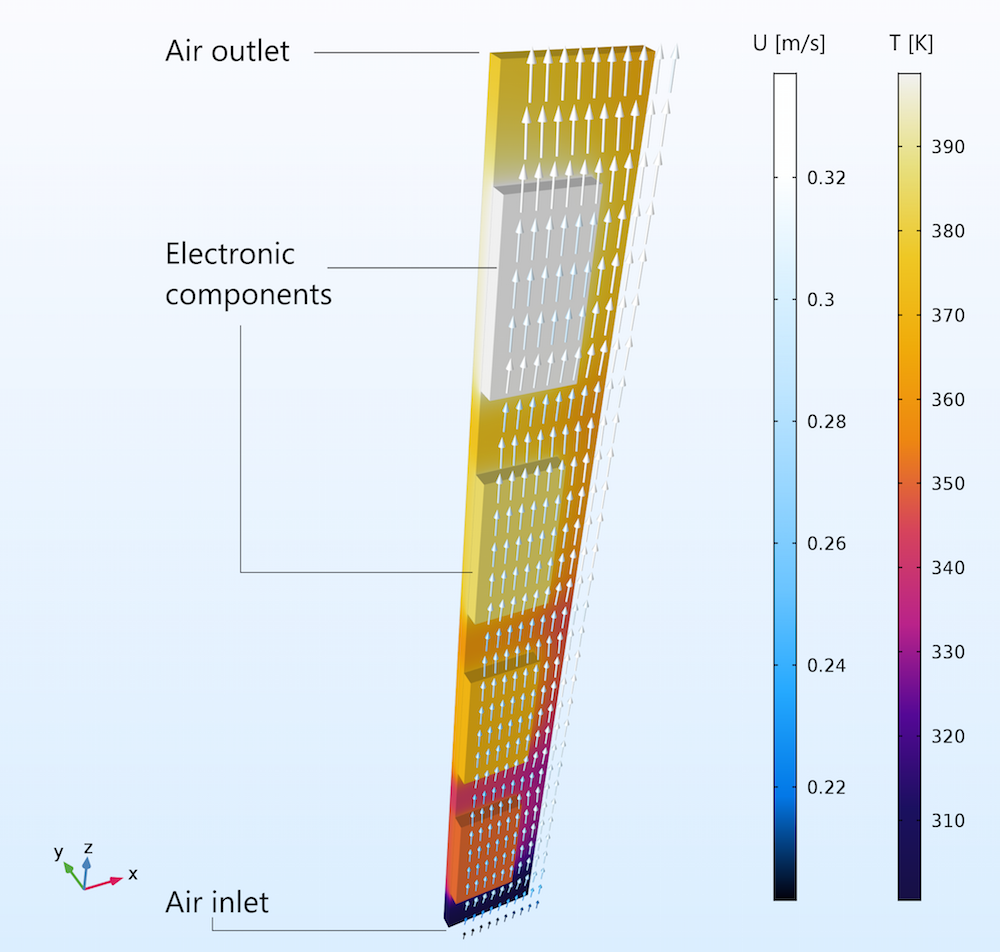
垂直电路板之间由浮力驱动的对流。我从箭头颜色中观察到膨胀,入口处的流率大约是 0.2 m/s,出口处约为 0.3 m/s。
使用 Boussinesq 近似的不可压缩流动选项
当密度变化对速度场的影响很小时,我们可以使用 不可压缩流动 选项的 Boussinesq 近似描述自然对流。这意味着通过将流体处理为不可压缩流体,连续性方程甚至比使用弱压缩流动 选项更简单。在这个示例中,连续性方程可以简化为:
(6)
在重力相反方向(默认为 z 方向)的动量方程中引入了一个体积力,用于考虑微小的密度变化。在给定参考温度下,通过将流体密度线性化,获得密度的微小变化。体积力的 z 分量变为以下形式:
(7)
其中 g 是重力常数,\[{\rho _{{\text{ref}}}}\] 是给定参考温度下的密度,α 是流体的热膨胀系数,ΔT 是测量温度与参考温度的温差。
使用 Boussinesq 近似描述浮力驱动的对流的好处是:流体流动方程中的非线性减少,问题的迭代次数减少,可以采用更长的时步求解瞬态问题,因此更容易对问题进行数值求解。
使用 Boussinesq 近似描述的一个典型对流案例:模拟温差相对较小的液态水。下图显示了从下方加热的水杯内的自然对流。示例中的流动模式非常复杂:靠近杯子中部和底部的水向上流动,垂直杯壁与杯子中部之间的水向下流动。
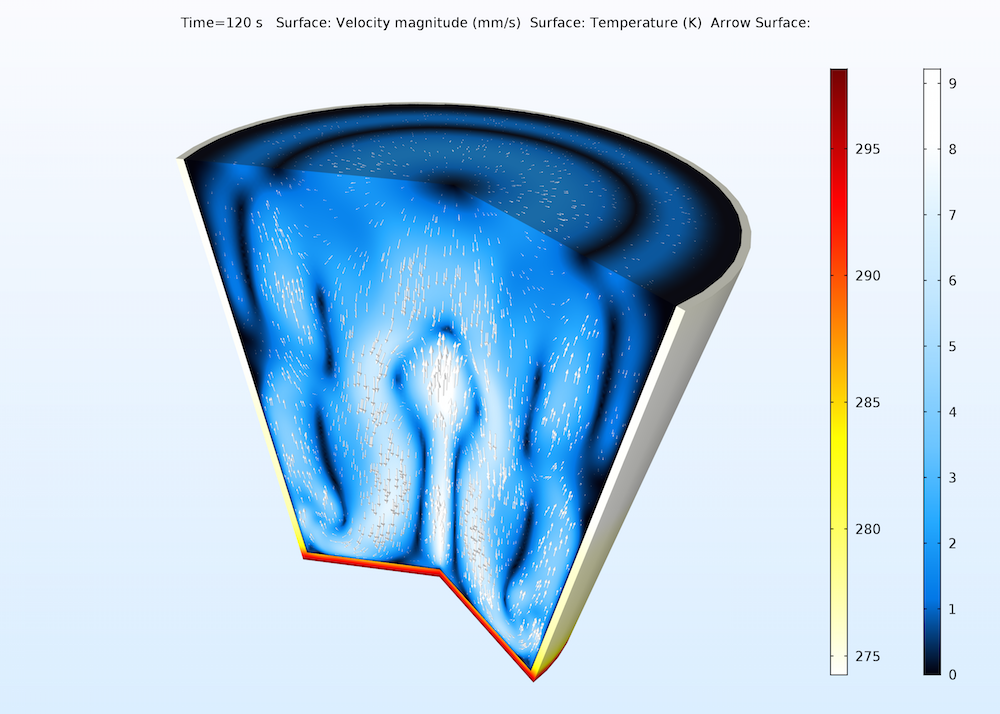
一杯水中的自然对流。绘图显示了杯中的速度场和玻璃壁上的温度分布。
在 COMSOL Multiphysics 中,在流体流动接口中选择如下设置就可以使用 不可压缩流动 选项中的 Boussinesq 近似描述浮力驱动的对流。
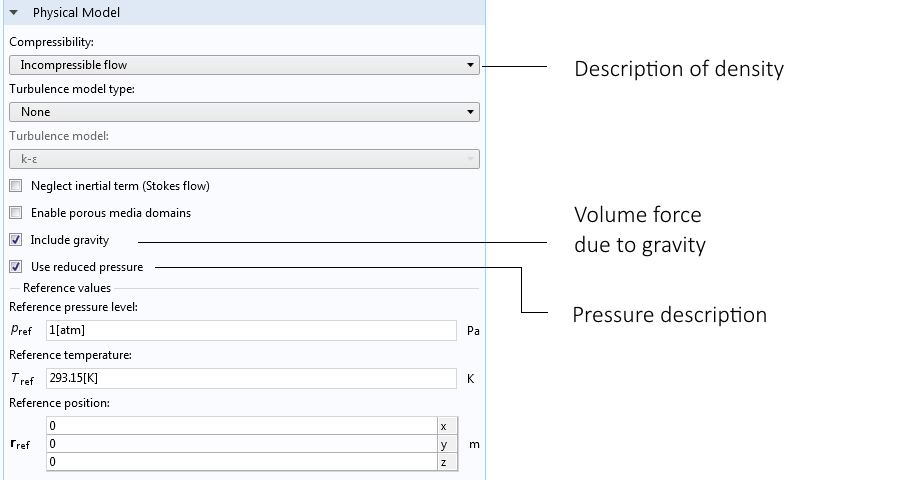
选择 不可压缩流动 选项和重力功能约化压力,就可以使用 Boussinesq 近似模拟自然对流问题。
约束自然对流模型中的压力方程
对模拟完全可压缩流动时,连续性方程需要考虑压力的时间依赖性,这是因为可压缩流体的密度是压力的函数。这也意味着,要获得一个良好定义的问题,通常只要包含一个压力的初始条件就够了,即使没有在边界上指定压力。
根据上文的讨论可知,对于弱可压缩流动和不可压缩流动的情况,连续性方程中随时间变化的压力项被忽略。如果没有设定压力的边界条件,压力场就会变得不确定,除非将它设定在域内的某一点上。
在 COMSOL Multiphysics 中,我们可以使用压力点约束,来规避不确定的压力场。在求解自然对流问题时,参考压力点缺失往往是造成收敛问题的根源。
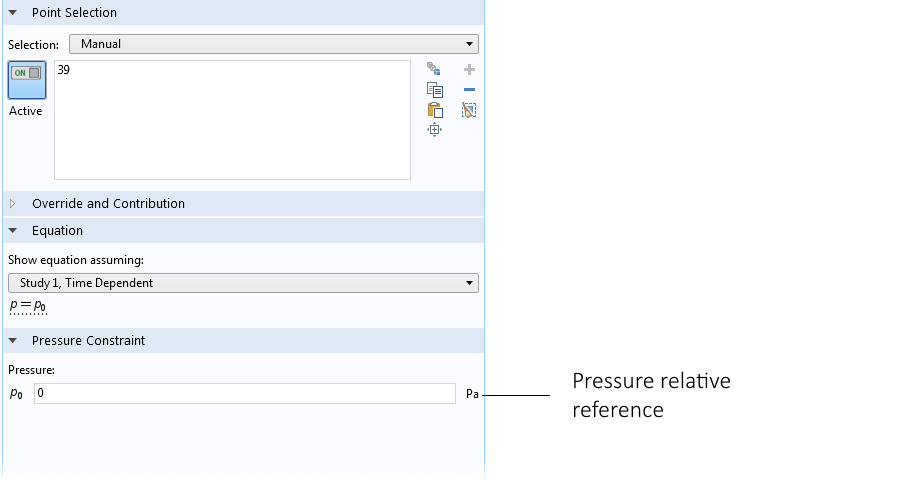
玻璃杯水示例中压力点约束的设置窗口。
利用耦合或解耦策略求解自然对流问题
描述自然对流的方程一般包括动量方程、连续性方程、能量传递或质量传递方程。如果浮力由温差驱动,能量方程与流体流动方程(Navier-Stokes 方程)完全耦合。对于自然对流,这种耦合属于高度耦合。这意味着使用 COMSOL Multiphysics 的全耦合求解器是最稳健的求解方法。
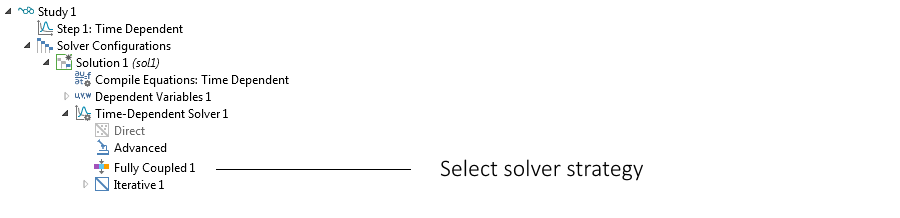
模型树中,包含完全耦合求解器选项的求解器。
对于大型问题而言,分离式求解器或许是更好的选择。举例来说,如果案例中包含许多化学物质,并且浮力是由于化学成分不同引起的密度差而造成的,那么分离式求解器或许是唯一可行的方法,因为它的求解过程不会消耗过多的内存。
结语
最后,我想用另一个生活中的自然对流问题来结束这篇文章。我在 抽烟时经常会想到思考对流问题。当然,我并不是提倡抽烟,但我最感兴趣的自然对流问题。下图为一根搁在烟灰缸上的点燃的香烟,图像显示了由燃烧产生的热量造成的气流分布情况。
烟灰缸上,点燃的香烟周围的自然对流(受到轻微外力)。
实际上,香烟燃烧产生的一部分流动属于强制对流,因为大部分烟草燃烧后会变成烟雾,从而使流体密度从约 500 kg/m3 ~1000 kg/m3 下降到了1 kg/m3 。这可以定义为烟灰及香烟周围空气边界的流体流动的入口流速。
扩展阅读
- 浏览“COMSOL 博客”,了解更多关于自然对流和流体流动建模的知识:



评论 (10)
一 王
2017-09-24电路版散热模型能发一个给我吗?邮箱cetc2016@163.com
Sologun
2017-10-02Can I ask how to get Eq.4?I mean the second term in Eq.4
Christian Wollblad
2017-10-02 COMSOL 员工Dear Jialong Wang,
Equation 4 is just an expansion of equation 1 using equation 3 and the ideal gas relation rho=pM/RT. So the last term is what remains of the term rho*div(u) after the equation has been divided by the factor pM/RT.
Best regards
Christian Wollblad
COMSOL
Sologun
2017-10-02But I got an extra term of -T*grad(p)/p*u
钢 罗
2018-06-12您好! 请问能把散热器和烟的案例发给我一下吗?564558817@qq.com 万分感谢~!
Tengyue Gao
2018-10-19罗钢,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
佳月 孔
2021-09-13请问压力点约束一般怎么设置,对于密闭腔弱压缩流体的压力点约束设置在哪儿比较好呢?
Haoze Wang
2021-09-13 COMSOL 员工孔佳月,您好!
压力约束点一般设置在压力梯度变化较小的区域,您可以参考此案例:http://cn.comsol.com/model/buoyancy-flow-of-free-fluids-665。
婉怡 杨
2023-10-18您好,我想问一下如何利用comsol内置函数,自己推导出实现热场和力场的耦合公式或者模型呢
Yi Li
2023-10-24 COMSOL 员工杨婉怡,您好!
COMSOL中内置了热力耦合的模型,详细可以参见:https://cn.comsol.com/blogs/course-modeling-joule-heating-with-thermal-expansion
如果想要使用自己推导的模型,可以考虑基于方程进行建模,可以参见:https://cn.comsol.com/video/equation-based-modeling-with-comsol-multiphysics-webinar-cn