
从 COMSOL Multiphysics® 软件 5.6 版本开始,在半导体模块中,我们将薛定谔方程物理场接口的功能从单分量波函数扩展到了多分量波函数。这样就可以对更广泛的系统进行仿真,例如带自旋的粒子和带有 3 个 p 形轨道混合的价带结构。在这博客文章中,我们使用了一个简单的基准模型来说明如何使用此多分量波函数功能。
哈密顿矩阵
当波函数具有多个分量时,哈密顿算子(the Hamiltonian)变为对波函数分量的矢量进行运算的矩阵。例如,瞬态薛定谔方程现在变成
(1)
其中,N 是波函数分量的数量。
等式右侧时间偏导项的负号是由于 COMSOL Multiphysics 中的所有物理场接口都采用了工程符号约定 exp(-i k x + i \omega t) 而非物理场符号约定 exp(i k x – i \omega t)。稍后,我们将因此而看到动量算子的符号也不同于大多数教科书中的符号。
通常,哈密顿矩阵的每个单元 \mathbf{H}_{mn} 可以包含零阶偏导项、一阶偏导项或二阶偏导项:
(2)
{\partial r_j}+ H^{mn(0)}(\mathbf{r})\right]
其中, m_e 是电子质量; \mathbf{r} 是位置矢量 \mathbf{r}=\{r_1,r_2,r_3\}\equiv\{x,y,z\}; A,H^{(1R)},H^{(1L)} 和 H^{(0)} 是可能在空间上变化的系数。
在第一项中,左侧的微分算子被理解为同时作用于系数 A 和波函数分量 \psi_{n}。同样,第二项中的微分算子作用于 H^{(1R)} 和 \psi_{n}。请注意,如前面所讨论的,所有动量算子都是通过常规约定当中的负号来区分的。
哈密顿矩阵的单元数量随着波函数分量数量的平方而增长。如方程2所示,每个单元可以包含各阶偏导项。为了提供灵活有效的方式在有限的窗口大小内将这些项输入到图形用户接口中,COMSOL 从 5.6 版本开始创建了许多内置功能。在下面的示例模型中,我们将展示如何使用这些功能。
模型系统
如上所述,哈密顿矩阵单元中的所有系数都可以在空间上变化。在异质结和纳米结构(例如量子线和量子点)中尤其如此。为了简单起见,我们选择了一个均匀应变的块状晶体模型,其中所有系数都是空间均匀的。尽管如此,这个简单的模型仍然用于说明将哈密顿矩阵单元输入到用户接口的过程。此外,它还可以作为基准模型,通过此简单系统的解析解来验证数值解。
氮化镓(GaN)是一种重要的直接带隙半导体材料,适用于光电子、高功率和高频应用。Chuang 和 Chang 在 1996 年发表了他们对包括 GaN 在内的纤锌矿晶体的 6×6 阶哈密顿矩阵的推导和计算方法(参考文献1)。在文献的方程(45)中,对 6×6 阶哈密顿矩阵进行块对角化,并且左上方的 3×3 矩阵如下,
(3)
F & K_t & -i H_t \\
K_t & G & \Delta-i H_t \\
i H_t & \Delta+i H_t & \lambda \\
\end{array}\right]
矩阵单元由参考文献1中的方程(34) 和 (42) 给出。例如,哈密顿矩阵的(1,1)位置上的单元是
(4)
前两项是数字,另外两项包含算子和数字:
(5)
{2m_e}\left[A_1 k_z^2+A_2(k_x^2+k_y^2)\right]+\lambda_\epsilon
(6)
\left[A_3 k_z^2+A_4(k_x^2+k_y^2)\right]+\theta_\epsilon
为了与文献中图5 所示的结果进行比较,我们将设置晶体动量的 y 分量为 k_y 零。对于薛定谔方程 接口,另外两个分量 k_x 和 k_z 分别由偏导数和代替(请参阅脚注)。因此,上面的两个方程变为
(7)
i\frac{\partial}{\partial z} A_1 i\frac{\partial}{\partial z}
+ i\frac{\partial}{\partial x} A_2 i\frac{\partial}{\partial x}
\right]+\lambda_\epsilon
(8)
{\partial z} A_3 i\frac{\partial}{\partial z}+ i\frac{\partial}
{\partial x} A_4 i\frac{\partial}{\partial x}\right]+\theta_\epsilon
最后,由应变贡献的项是
(9)
(10)
其中,\epsilon 是应变分量。
参考文献1 的表 III 中列出了能量参数 \Delta_1 和 \Delta_2、有效质量参数 A_1〜A_1,以及变形电位 D_1〜D_1 。
利用方程7 和 方程8,为 3×3 哈密顿矩阵在(1,1)位置的单元 F 展开方程 4 ,我们得到
(11)
\left[i\frac{\partial}{\partial z} (A_1+A_3) i\frac{\partial}{\partial z}
+ i\frac{\partial}{\partial x} (A_2+A_4) i\frac{\partial}{\partial x}
\right]\Delta_1\Delta_2+\lambda_\epsilon+\theta_\epsilon
经过整理之后将所有的算子都写到第一项中,其他四项只包含变量。
数值和解析方法
在参考文献 1的图5中,绘制了未发生应变和发生应变的晶体沿着 k_x 和 k_z 方向的价带变化,其中设置 k_y 为零。由于所考虑的系统是块状晶体,k_x 和 k_z 只是数字,因此 方程(3) 中的哈密顿矩阵简化为对应于给定值 k_x 和 k_z 的某些特定数值的 3×3 矩阵。可以通过数值计算该矩阵的特征值以获得图中所示的能带结构。这是本文采用的分析方法,将用于验证接下来要讨论的数值方法。
在一般的非均匀结构(例如量子阱和量子点)中,如前所述,数字 k_x 和 k_z 必须由偏导数 i\partial / \partial x 和 i\partial / \partial z 代替,求解 xz 平面上的薛定谔方程以获得能带结构。这是数值方法。当然,对于块状晶体的简单系统而言,这有点大材小用。但是,出于教学和验证的目的,我们选择了这个简单的系统。一旦你学会了如何使用物理场特性来构建此简单模型,就可以模拟只能通过数值方法求解的更复杂的系统。
COMSOL Multiphysics® 模型
由于哈密顿矩阵大小为 3×3 ,因此可以在模型向导或物理场接口设置 窗口中将波函数分量的数量设置为3是非常简单的。
如上所述,该模型在 x 和 z 方向是二维的。为了使模型符号表示更易于阅读,我们将第二个轴的坐标名称从默认 y 更改为 z,如下截图所示。
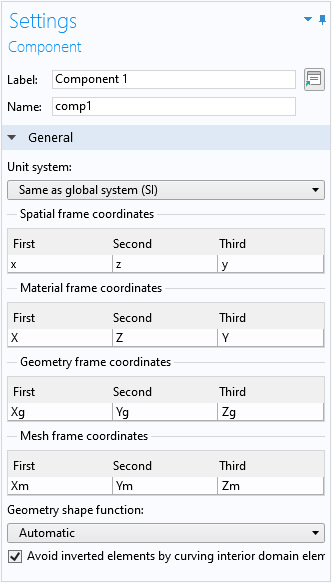
更改坐标名称以匹配感兴趣的方向(x 和 z)。
由于我们仅对区域中心附近的能带结构感兴趣,因此我们可以使用比元胞稍小的简单正方形域,并对薛定谔方程使用 Floquet-Bloch 周期边界条件。在这种状态下,问题接近一个均匀的连续体,并且少量的网格单元就足够了。(在结构相关的模型中也可以使用改网格剖分方法,具体参见薄膜体声波(BAW)结构的教程模型。)
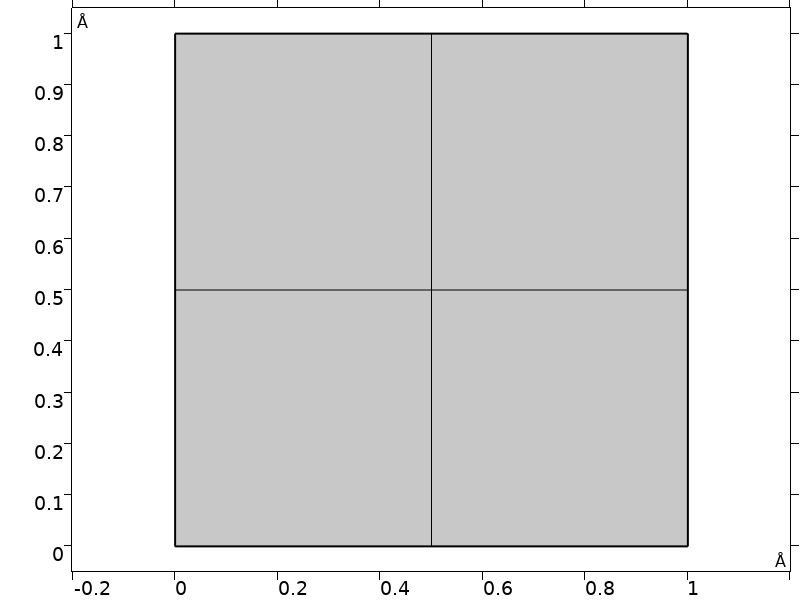
模型中的仿真域和网格。
为了方便地创建一个绘图以与文献的图5 进行比较,我们设置了扫掠参数 kp,当其为正时表示 kx 轴,当其为负时表示 kz 轴。如下截图所示,为了实现此目的,我们使用在 kx 和 kz 的表达式中使用if语句。
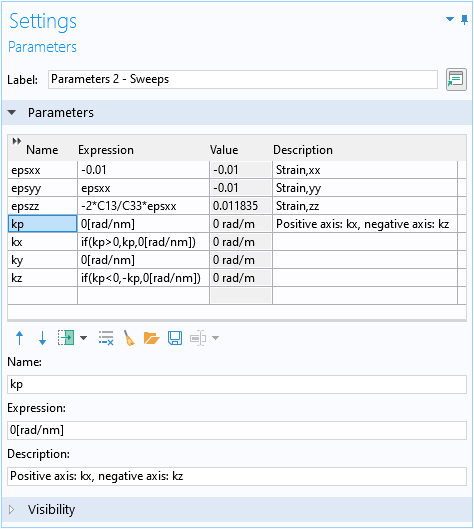
为 kx 和 kz 的双轴一维绘图设置参数 kp 。
解析解
对于解析方法,我们建立了一个全局方程来对 方程3 给出的 3×3 哈密顿矩阵进行对角化,且使用保留名称 lambda 作为全局方程的特征值。我们用 1meV 的能量大小对哈密顿进行缩放,以使源项的值接近于 1,且特征能量是以meV为单位的特征值。我们还在表达式中添加了一些空格来使矩阵的列对齐。
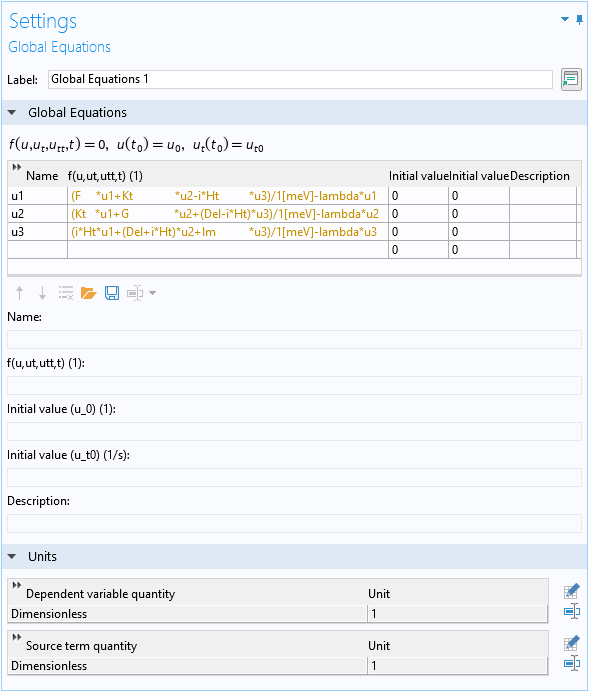
查找 3×3 矩阵特征值的全局方程。
因为此时尚未定义特征值变量 lambda,因此文本为黄色。
求解薛定谔方程
如前所述,数值方法可用于求解薛定谔方程。为了方便地创建一个绘图以与文献的图5进行比较,我们将特征值大小设置为与图形的垂直轴相同的能量单位(meV),以便特征值取相同单位(meV)中特征能量的数值。
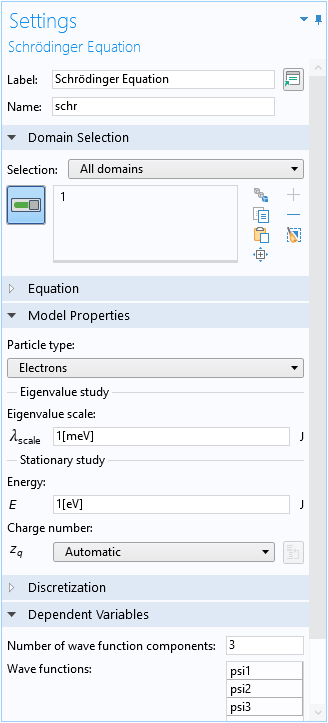
薛定谔方程物理场接口的设置窗口。
哈密顿矩阵输入
现在,我们准备输入 3×3 哈密顿的矩阵单元。同样,我们以位于(1,1)位置的单元为例。方程11 中总结了该矩阵元的所有项。第一项包含二阶谝导,因此我们添加了二阶哈密顿域条件。此功能自 COMSOL Multiphysics 5.6 版本起被引入,同时具有处理薛定谔方程物理场接口的多分量波函数的功能。
该域条件的设置窗口中的主要功能是哈密顿输入表。该表的前两列用于输入哈密顿矩阵单元的行索引和列索引。从下拉菜单中选择每个索引,该菜单会自动从 1 填充到 N (波函数分量的数量)。例如,在这里我们已经将设置 N 为 3,因此下拉菜单可以选择 1、2 或 3。在开始向表中输入数据之前,请务必确定并设置波函数的数量(请参阅下面的已知限制部分)。
第三和第五列用于两个微分算子。它们还作为下拉菜单提供,根据模型的空间维度自动填充微分算子。在这里,我们在 xz 平面上建立了二维模型,因此选择是 i\partial / \partial x 和 i\partial / \partial z。
第四列是有效质量参数 A。与 COMSOL Multiphysics 中几乎所有其他输入字段一样,该输入字段接受数字、参数、变量或任何其他数学公式。所有的域条件中都内置了 \hbar^2/2m_e 因子,包括当前域,即一阶哈密顿,左,一阶哈密顿,右和零阶哈密顿。
最后一列描述,我们可以输入对每一个表达式的解释。哈密顿矩阵中的每个单元,例如 方程11 当中给出的单元 F,包含不同类型的项,这些项将输入到几个不同功能的多个表格行中。因此,通过在描述列中输入适当的注释来解释每一行是非常重要。
下列截图显示了域条件的设置窗口,其中将等式11 的第一项输入到哈密顿输入表的前两行。矩阵单元 F 的位置是(1,1),因此行索引和列索引均为1。表中两行的微分算子和 A 参数对应于 方程 11方括号中的两项。描述列解释贡献源;在本例中,这两行来自方程4的 F=\lambda+\theta 部分 。
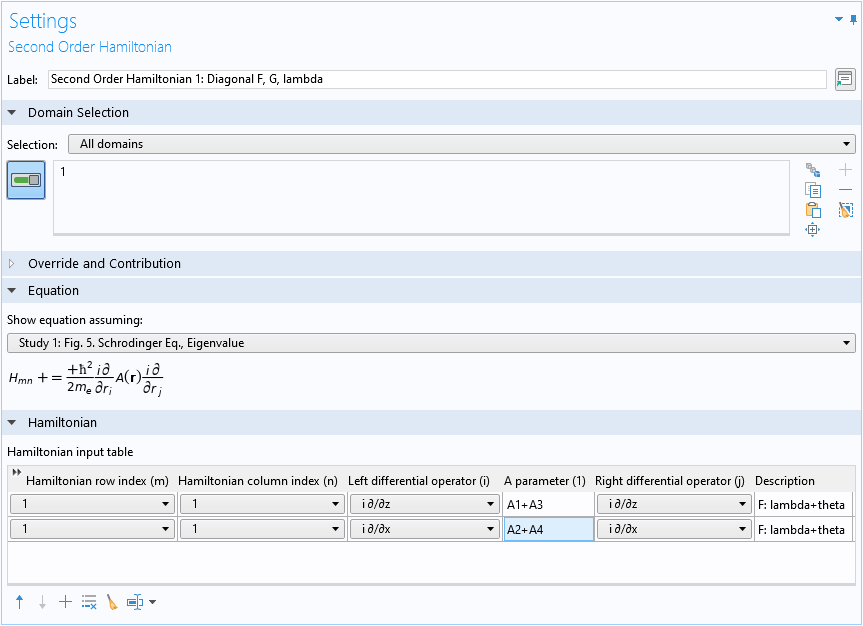
二阶哈密顿域条件的设置窗口,带有输入矩阵单元的第一项。
复制/粘贴表格行
在输入(1,1)单元 F 的其余项之前,我们注意到(2,2)单元 G 的二阶算子部分与之一相同 。参考文献1的等式(34) 为:
(12)
因此我们得到了对二阶哈密顿(G=\lambda+\theta)的相同贡献,只是他们位置不同:现在是(2,2),而不是(1,1)。
我们可以复制并粘贴 F 的两行数据并将行和列索引更改为2,而无需重新输入两行数据。首先,单击并拖动鼠标以选中表中的两行:
然后右键单击以复制选定的行:
然后单击添加按钮以添加新行:
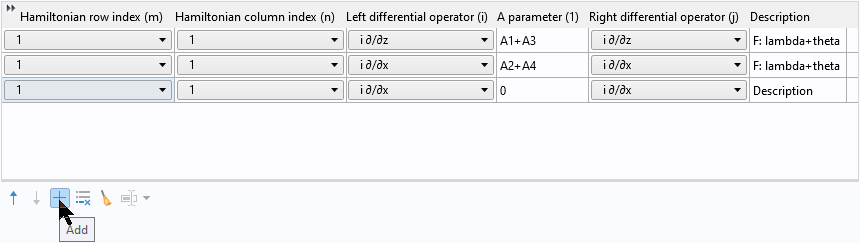
然后右键单击以将两个复制的行粘贴到表中:
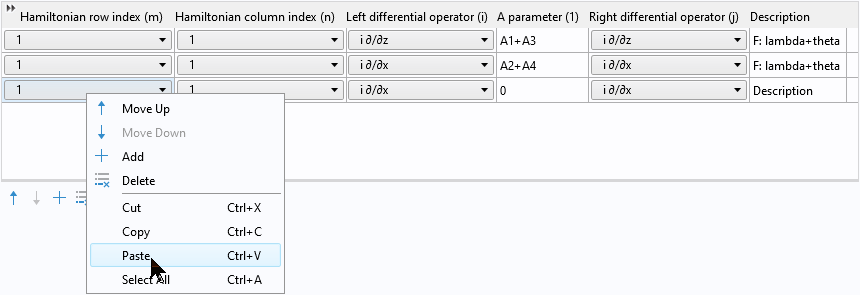
粘贴后,我们就有了两对相同的行:
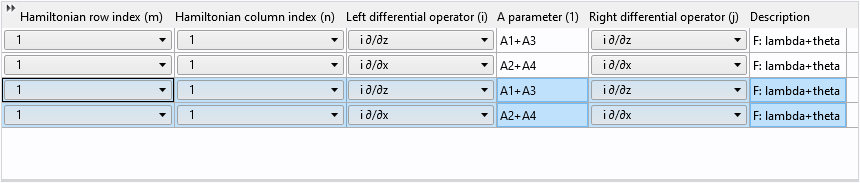
最后,将行和列的索引从1更改为2并更新描述:
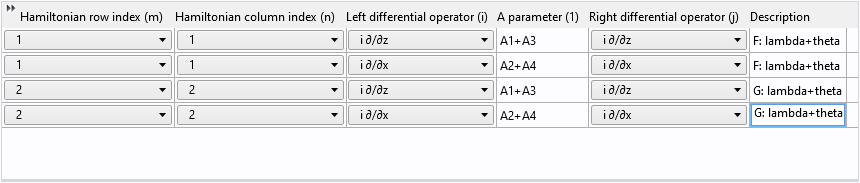
以这种方式重用表格行不仅可以节省时间,而且还有助于避免错误!
禁用默认有效质量贡献
我们刚才以为对角元为例演示的二阶哈密顿域条件的使用,对应于通常由默认有效质量特征所描述的动能项。我们应该禁用它以消除不必要的默认哈密顿贡献。
禁用默认的有效质量特征,以消除其对哈密顿的不必要贡献。
没有算子的项
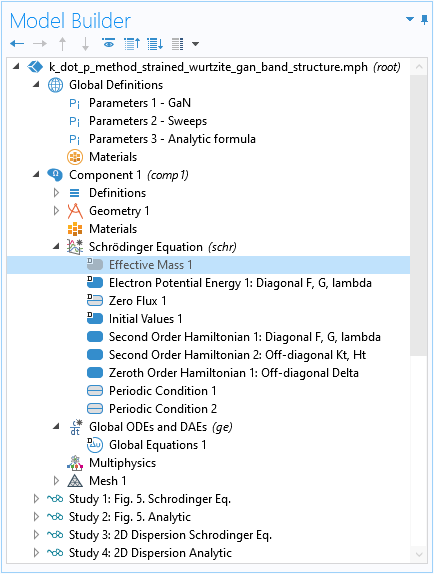
如下截图所示,因为该元素位于哈密顿矩阵的对角线上,所以为了输入(1,1)单元的其余项 F(等式11 中的最后 4 项: \Delta_1+\Delta_2+\lambda_\epsilon+\theta_\epsilon)(仅是变量),我们可以使用零阶哈密顿 域条件或者是默认的电子势能域条件。
对哈密顿矩阵的对角元的零阶项使用默认的 电子势能域条件。
非对角元
对于非对角元,我们按照相同的程序填写二阶项哈密顿输入表:

零阶项:

如前所述,零阶哈密顿量具有内置 \hbar^2/2m_e 的前因子,如果输入量(本例中为 Del)是一个能量单位,则需要将其除以前因子。
已知限制
如果在哈密顿矩阵输入表中填入数据后更改了波函数分量的数量,则表格行将变得不同步。此时,需要清除表格并再次填充数据。在用数据填满任何哈密顿输入表之前,我们建议您先确定要在模型中研究的特定哈密顿矩阵,然后输入相应的波函数分量数。
其他设置
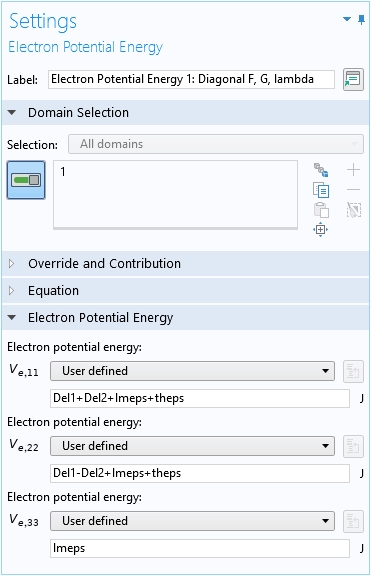
设置 Floquet-Bloch 周期边界条件以创建简单的映射网格,并使用特征值研究中使用提前定义的参数 kp 来对波矢量进行扫描。这是很简单的。
若要求解配置有全局方程的解析 3×3 阶矩阵方程,请使用所有特征值选项以获得 3×3 阶矩阵方程的所有 3 个特征值。
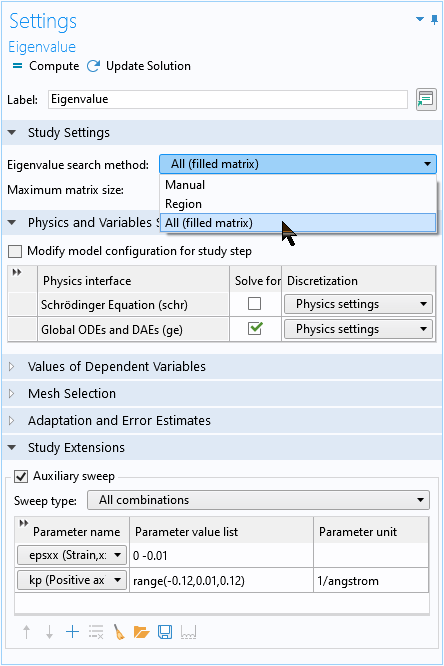
使用 所有特征值选项可获取全局方程的所有3个特征值。
未发生应变和发生应变的纤锌矿晶体的已计算能带结构
以下两个图显示了计算得到的未发生应变和发生应变的沿正 kx 轴和负 kz 轴方向已计算的重空穴(HH)、轻空穴(LH)和晶体场分裂空穴(CH)的能带分布,其与参考文献 1的图5 当中的解析解(圆圈)吻合较好。
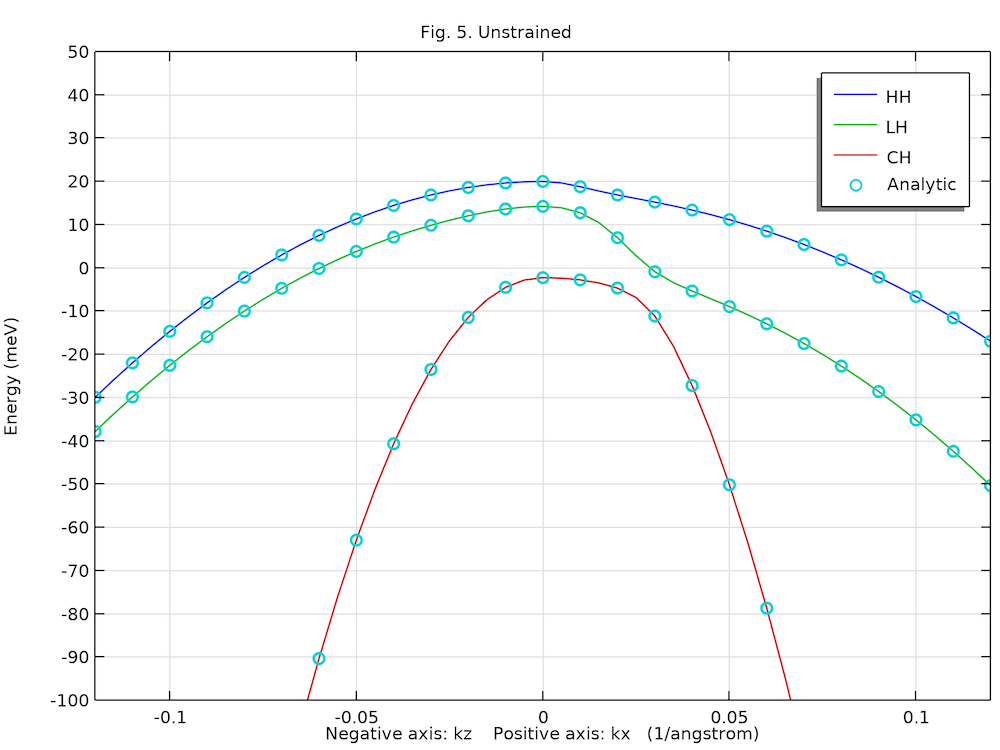
块状GaN纤锌矿晶体未发生应变的价带结构。
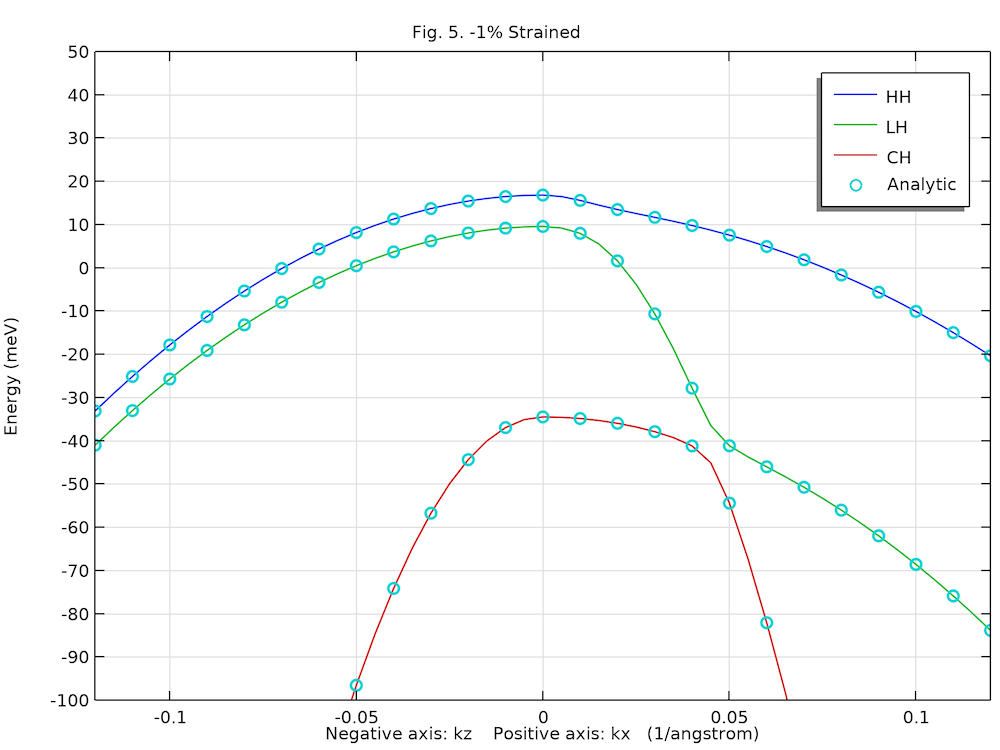
块状 GaN 纤锌矿晶体的压缩应变价带结构。
下图比较了计算值(彩色表面)和解析解(灰色线框)之间三个价带沿x和z方向的二维能量表面。两者吻合的也很好。
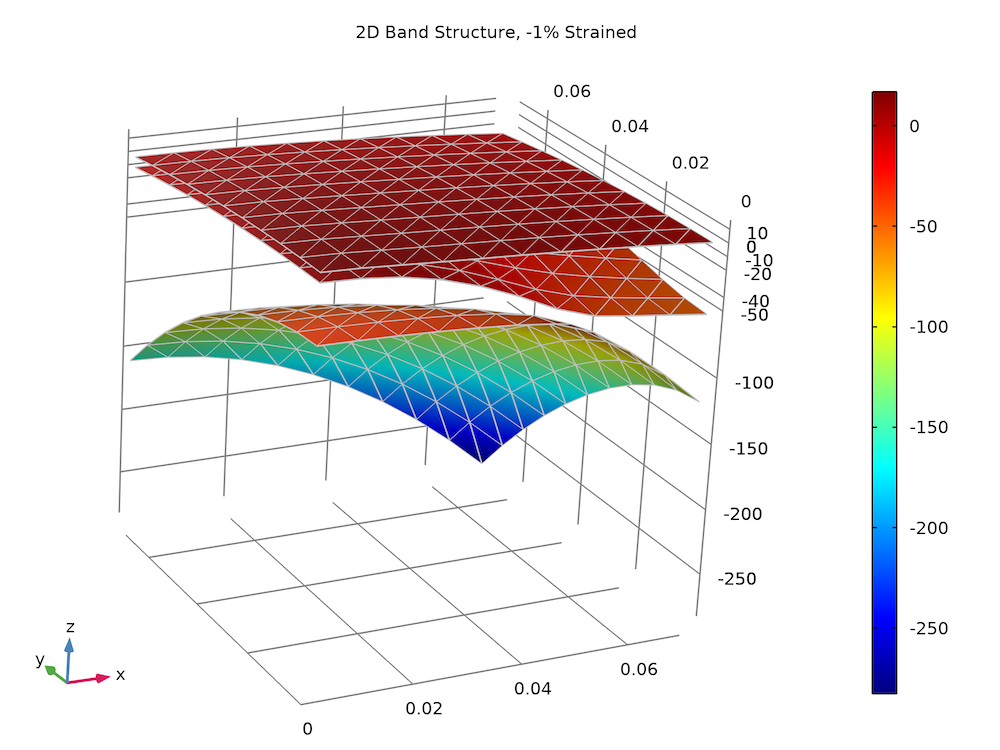
块状 GaN 纤锌矿晶体的应变价带结构。
结论
在此博客文章中,我们使用一个简单的块状晶体示例演示了薛定谔方程的物理场接口处理多分量波函数的新功能。使用内置功能将哈密顿矩阵系统地输入到软件接口中。同样的方法可以应用于更复杂的系统,例如量子阱和量子点。我们很想知道您如何在仿真项目中使用这项新功能!
动手尝试
单击下面的按钮,尝试自己建模。您将进入 COMSOL 案例下载页面,其中包括详细步骤文档和 MPH 文件。
参考文献
- L. Chuang and C.S. Chang, “k·p method for strained wurtzite semiconductors,” Phys. Rev. B, vol. 54, p. 2491, 1996.
脚注
回想一下,因为 COMSOL 的时间相位符号约定为 exp(+i \omega t),所以平面波是 exp(+i \omega t-i k_x x)。因此,使用的算子为 +i\partial / \partial x,而不是 -i\partial / \partial x 。






评论 (0)