把比水轻的球丢入装有水的小烧杯中后，当球在水面上漂浮时，如何模拟水面的形状和球体的运动？本文我们演示了如何在 COMSOL Multiphysics® 软件中对该系统进行建模。尽管我们考虑的是小球体的情况，但此处所用讨论的技术同样适用于其他较大的结构。
浮球的振荡运动：一个 计算流体力学（CFD）问题
首先，将一个浮球放入一个盛满水的烧杯中。球体的半径为 0.15cm，密度为 800kg/m3，最开始悬浮在空气中。 圆柱形烧杯的半径为 0.65cm，高度为 1.7cm，装有部分水。由于该系统的尺寸足够小，因此假设流动模式为层流是合理的，这也使我们能够在普通计算机上实现快速计算。我们可以用完全相同的方式对较大的系统建模，但需要更多的计算资源。
为了模拟球体穿过水面的运动过程，我们需要对空气相以及水相中的流体流动进行建模。如果将球体视为刚体，则可以通过求解常微分方程(ODE)来计算其运动。常微分方程描述了球体从空气中掉落，撞击水面，并最终与空气和水相互作用过程中的受力情况。流体在固体边界上施加的总流体应力为：
(1)
式中，ufluid 表示流体速度场，p 表示流体压力，μ 表示流体的动态黏度，n 表示边界的向外法线，I 表示单位矩阵。
在一个充满水的烧杯中，浮球悬浮在水面上方的空气中。隐藏了烧杯壁的一部分以显示球体。
假设球体仅沿垂直方向（z）运动，我们可以建立如下方程：
(2)
F_z &= m g + m\frac{d v_{s}}{d t}\\
v_s &= \frac{d u_s}{d t}
\end{align}
式中，m 表示质量，vs 表示在 z 轴方向上的速度，us 表示球体在 z 方向上的位移。
在球体表面上，对方程1 中的流体应力的 z 方向分量进行积分可得到力 Fz。将上述运动方程（常微分方程）与有限元模型一起求解，可以计算球体的位移和速度。
由于球体会在空气以及水中运动，为了同时模拟两种流体，我们在随时间变化的空间坐标系 中建立了两相流模型。空间坐标系是一种常见的、固定的全局欧式系统，其坐标系为(x，y)。这些与流体域的网格节点相对应的空间坐标系是时间的函数，表示空间某一点当前的位置。这可以通过在动网格 接口中求解流体流动问题来实现。
球与流体接触面处的网格位移等于球体的位移。在流体域内部，基于动网格 接口中合适的平滑算法来计算网格变形：
(3)
在球体与流体边界上，流体速度由下式计算：
(4)
在 COMSOL Multiphysics® 中建立模型
对于上述问题，我们可以建立二维轴对称模型。为了对此问题进行建模，我们将方程1 – 4作为表达式，将两相流 接口与动网格 接口以及全局方程式进行耦合。
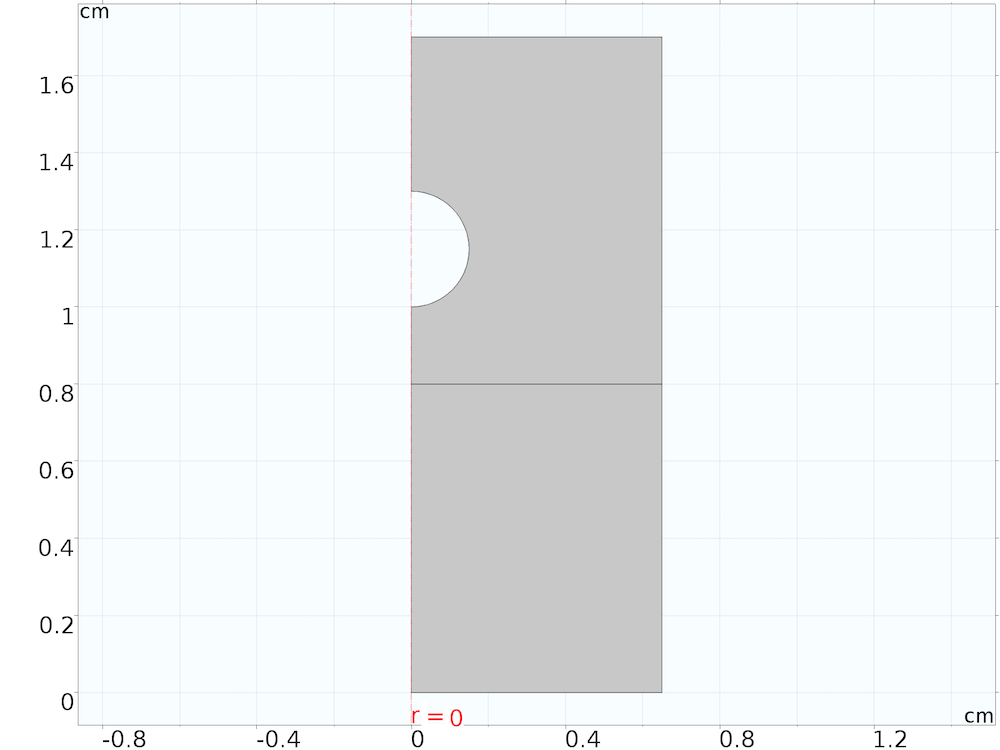
二维轴对称模型的几何形状，用水平线表示水面的初始位置。在常微分方程中，我们将球体视为刚体，因此可以定义球体为模型域的边界。
在此模型中，空气相以及水相中的流体流动均为层流，因此我们可以使用层流两相流，相场 接口（阅读此博客，了解有关如何选择多相流接口的更多信息。）该多物理场接口自动定义了层流和相场之间的耦合，可以用来追踪水面形状变化的细节。
通过层流两相流，相场 接口，我们可以将球体的边界条件看作移动的润湿壁进行模拟。通过相场接口的润湿壁 边界条件，我们可以设定水面与球体壁之间的接触角；而在层流 接口中，通过使用壁边界 条件中的壁移动 设置，我们可以设定球体壁的移动速度，在该烧杯的顶部使用出口边界条件。
下图显示了模型设置的结构和各种接口（即层流，相场，和动网格）：
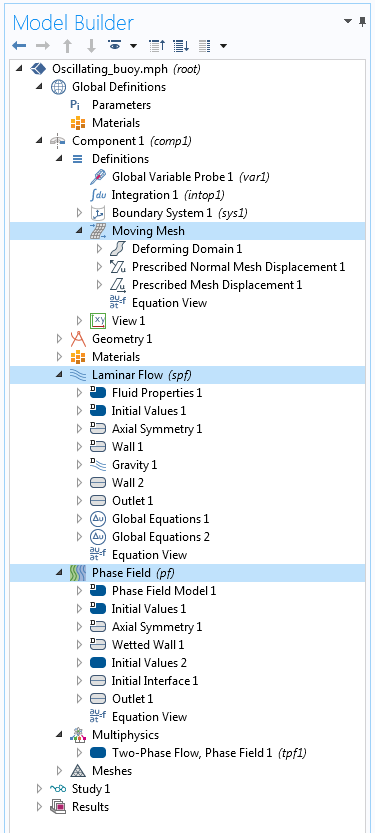
在相场接口中，对于初始设置，我们将相场变量的值设定为 Φ=1（流体1为空气）和 Φ=-1（流体 2 为水），水平线代表初始时刻的水平面，即初始时刻的两相界面。水平线上方为空气，下方为水。初始设置如上图所示。
我们利用润湿壁 边界条件来设定两相界面在烧杯壁以及球体壁上的接触角。为简单起见，我们假定烧杯壁以及球体壁上的接触角相等。
流体中的速度场会自动耦合至相场中来解释对流。在层流 与相场 接口耦合的多物理场接口中，设定流体的属性和表面张力系数。
动网格 接口计算了流体域中由于球体运动而导致的网格变形。我们还使用了边界条件来描述流体边界处的网格应如何变形。这里重要的边界条件是网格位移，它等于球体边界上的位移(方程3)。
球体的运动完全归因于重力载荷。然而，流体施加了方程1中所定义的曳力。该曳力 z 方向上的分量可以通过在整个球体表面上对内置变量进行积分得到。内置变量 spf.T_stressz 用于计算周围流体施加在球体表面上的总应力的 z 方向分量。
了解更过信息，请阅读博客如何计算升力和曳力。
使用全局方程式 接口求解 常微分方程（方程2）。下图显示了在全局方程式 接口中使用的方程式之一，其中 vs 是球的速度，如方程2所述。vst 是速度（或加速度）的时间导数，而 intop1 是在实体边界上定义的积分算子。
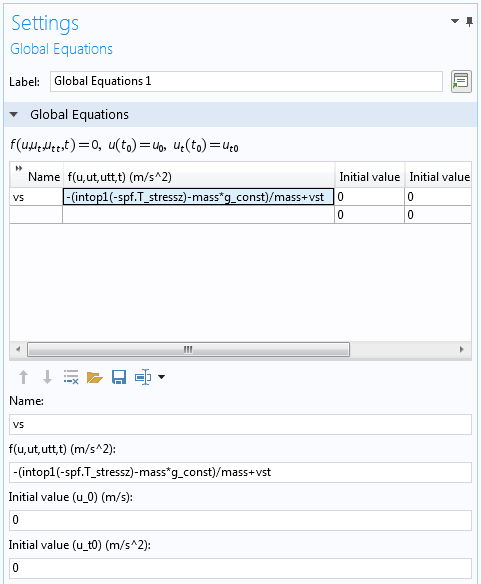
设置 全局方程式接口求解球的速度。
由于球体的移动较大，因此网格变形将很大。为了保持较高的单元质量并避免单元反转，我们可以使用“自动重新划分网格” 功能。该功能可以基于网格质量暂停瞬态计算，并在继续计算之前重新划分当前网格。
仿真结果分析
下图显示了落在水面上的球体，水-空气界面（Φ= 0.5）以及流体速度的横截面图。
充满水的烧杯中的浮球的运动，水面和流体速度大小的横截面动画。为了在仿真的后期看到速度幅度的变化，图例中颜色的最大限值为 0.1[m/s]。
下图为球体位移与时间的关系图。与预期一样，球体的运动受周围的流体阻碍作用，位移幅度随时间呈指数下降。
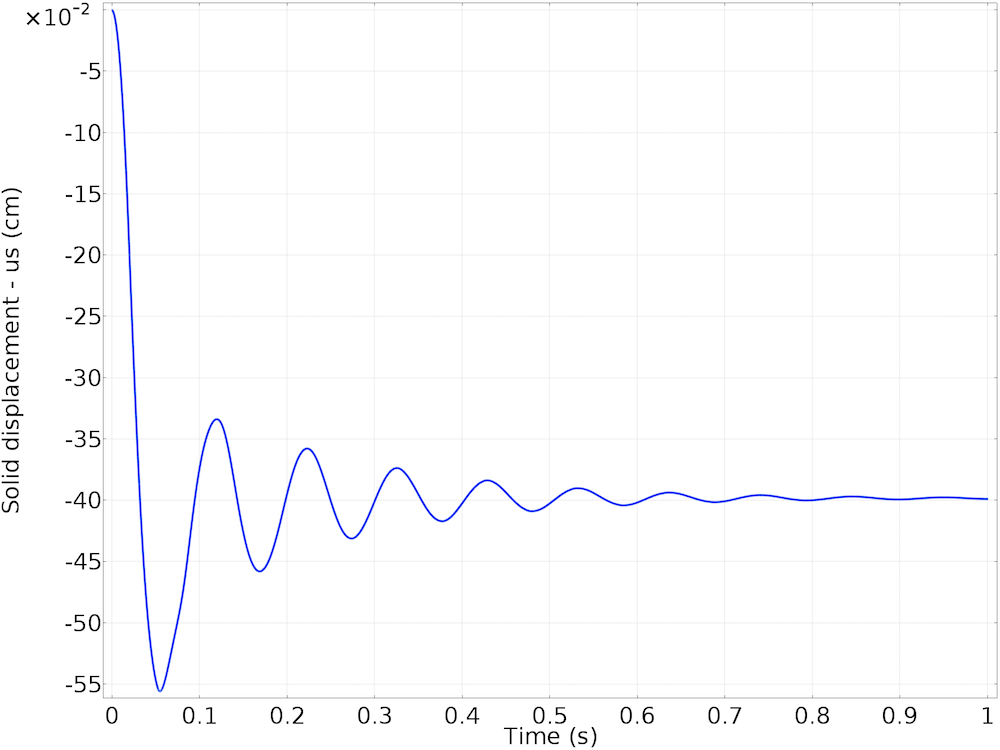
结语
在这篇博客中，我们演示了如何对浮球的振荡运动进行建模。文中，球体及其运动被看作是轴对称的，没有旋转运动。通常，如果需要，可以将此处讨论的建模策略应用于旋转和平移模型。对这种情况进行建模，需要使用常微分方程求解刚性物体的其他旋转运动。相反，使用固体力学 接口的内置功能来自动解决刚体运动会容易得多。该接口也允许模拟一个更大的系统，在该系统中，气流会变为湍流，并且可以在所有方向上产生运动。
单击下面的按钮，访问此博客中介绍的模型的文件：
评论 (51)
兆长 王
2020-08-06您好，可以请教您这些建模的问题么
hao huang
2020-08-06 COMSOL 员工您好，建模相关问题可发送邮件至 COMSOL 技术支持邮箱：support@comsol.com
聪 郑
2020-08-06你好，COMSOL有没有关于两个物体碰撞反弹的案例呢？不是这个案例中的两相流中的碰撞，而是两个物理刚性的碰撞反弹。谢谢！
屹磊 金
2020-08-20 COMSOL 员工在我们开放的结构力学培训课程中有关于两个物体碰撞反弹的演示。在课程第三部分的1小时54分处，课程链接：http://cn.comsol.com/video-training/structural-mechanics-cn-prt3
武智 元
2020-08-30您好，有无液滴碰撞固体壁面反弹的案例，谢谢！
hao huang
2020-08-31 COMSOL 员工您好，可参考案例”喷墨打印机喷嘴 – 水平集方法“：
案例链接：https://cn.comsol.com/model/inkjet-nozzle-8212-level-set-method-1445
在 COMSOL 开放的结构力学培训课程中有关于两个物体碰撞反弹的演示,在课程第三部分的1小时54分处,
课程链接：http://cn.comsol.com/video-training/structural-mechanics-cn-prt3
sa ali
2020-11-19您好，模拟落在水面上的球体模型案例文件没有可不可以发
Ying (Grace) Xu
2020-11-24您好，请查看下方链接下载：
http://cn.comsol.com/model/modeling-a-sphere-falling-on-a-water-surface-12655
sa ali
2020-11-25这我看了只有ppt,没有模型文件
Ying (Grace) Xu
2020-11-26很抱歉给您造成了困扰，经核实该案例中的 mph 文件目前暂未提供。
yi wang
2021-02-26如何在三维模型中的一个球体域（球体外壳带一层无限元）中，定义该球体域的上半球材料为空气、下半球材料为水的一个球体呢？有无相关案例？
背景：该球体域用于AC/DC模块，仿真浅水区中的天线在空气和水交界面附近的电磁场分布情况
kai zhang
2021-03-11 COMSOL 员工无限元域的添加可以参考案例：http://cn.comsol.com/model/simulation-of-an-electromagnetic-sounding-method-for-oil-prospecting-8607
该案例中是采用电磁波接口，因此用PML域描述无限大空间。
Lin Li
2021-05-10您好，有没有物体在空气中自由下落的详细案例
洋洋 张
2021-05-12 COMSOL 员工您的问题描述有些模糊，您可以将您的问题详细描述（包括是否考虑物体变形、空气流场分布等内容）发送至support@comsol.com，我们会有专业工程师为您解答。
Yong Qi Xu
2022-03-04您好，请问有没有给两相中的一相添加初速度的案例参考呢？比如说在空气中初始时刻就存在初速度的液滴，而不是像静止
靠重力加速的液滴。
另，相场、水平集和动网格比较的那个矩形板案例在案例中心中只有ppt，对矩形板的移动建模我也想了解
灿 李
2022-04-15您好，想问一下有没有具体的操作步骤。另外想问一下“不支持时间导数逐点约束。”该如何去解决。
越 赵
2022-08-08 COMSOL 员工您好，该博客模型暂时没有逐步的建模操作指导，您可以点击获取模型文件，在下载文件处下载pdf文件获取建模指导，并可以根据用到相同物理场的其他模型建模指导文件逐步建模。
晨杰 王
2022-07-23您好，有没有颗粒受到电场力和流体体积力运动的动网格的模型案例
越 赵
2022-08-08 COMSOL 员工您好，颗粒受到电场力和体积力运动的问题不需要使用动网格的方法来模拟，你可以使用COMSOL中的粒子追踪物理场接口来模拟该问题，建议您参考区带电泳案例：https://cn.comsol.com/model/zone-electrophoresis-47641。
亦凡 吴
2022-07-27请问是否有更多运动固体接触流体的案例（不考虑固体形变）以及如何仿真一些简单的流体固体接触过程中发生的拓扑变化（实际仿真过程中动网格的网格会反转）
越 赵
2022-08-08 COMSOL 员工建议您在COMSOL首页的搜索框中输入“FSI”或者“流固耦合”以获取更多的关于流固耦合的案例及博客。
方玲 梁
2022-09-22可以回复我的留言吗？ 谢谢！
方玲 梁
2022-09-22您好, 如果球体尺寸较大，如直径为3mm的五倍以上，球体密度也比水大，方程(1) (2)还适用吗??
越 赵
2022-10-10 COMSOL 员工您好，方程1描述了流体施加到固体表面的力，方程2描述了球体在受力下的运动方程，这两个方程和球体的直径和密度无关，均适用。
lucky 王
2022-09-23你好请问有没有关于带膜的物体在流体的运动呢
元举 牟
2022-10-11您好，有无小球受到电磁力驱动运动的相关案例呢，谢谢
Qihang Lin
2022-10-26 COMSOL 员工6.0 版本中新增磁机械力接口可以直接将两者进行耦合，参考案例：http://cn.comsol.com/model/102811
新成 宫
2023-03-02请问，是否有充满液体的复杂多路径单输入单输出的腔体，模拟一球体进入与排出的案例，谢谢希望可以得到您的回复，674826342@qq.com
Haoze Wang
2023-03-08 COMSOL 员工暂时无相似案例，建议参考本博客提供的思路完成建模。
猛 杨
2023-08-28您好，请问这种模型能否用流固耦合、相场模型一起做呢
Haoze Wang
2023-08-30 COMSOL 员工您好，相比于直接用ODE求解刚体的运动，使用流固耦合的求解难度会大一些，相关案例请参考两相流流-固耦合：http://cn.comsol.com/model/two-phase-flow-with-fluid-structure-interaction-4515
文杰 于
2023-11-071
Haoze Wang
2023-11-14 COMSOL 员工您好，此模型是二维轴对称模型，变量spf.T_stressz本身的单位是N/m^2，使用积分算子intop1后，单位是N
文杰 于
2023-11-08有这个mhp吗 我想看下方程一
hao huang
2023-11-14 COMSOL 员工发送电子邮件至 support@comsol.com ，获取模型文件。
文杰 于
2023-11-27你好我想问一下 我用流固耦合模拟二维球体在矩形管道竖直下落 管道上方给的压力出口，壁面均是无滑移壁面，材料给的刚体，质量给的ρπd^2/4，惯性矩给的ρπd^4/32，旋转中心选的质心，低Re数，40左右，为什么球体刚开始下落一直向右偏移啊，不是竖直下落。
Haoze Wang
2023-11-28 COMSOL 员工您好，建议检查划分网格是否对称，如果预期结果是竖直下落，建议利用网格用中的复制操作，将网格设置为关于中心轴完全对称的，以减少网格对结果的影响。
文杰 于
2023-11-28谢谢
文杰 于
2023-11-281
Haoze Wang
2023-11-30 COMSOL 员工您好，关于具体的模型问题，建议将您的模型发送至技术支持中心（https://cn.comsol.com/support），由专业的工程师调试模型后回复您。
一帆 吴
2023-12-31你好 我想问一下 我做三维动网格模拟球体在管道中沉降，为什么球体下落时，速度先增大 之后呈波动式一直减小啊，顶面给的压力出口 底面给的开放边界，球体受到重力，从顶面向底面沉降
越 赵
2024-01-02 COMSOL 员工您好，理论上，刚开始球体速度小，流体的阻力小，所以重力和阻力的合力向下，球体会加速，随着速度增大，阻力也会逐渐增大，合力逐渐变小，加速度变小，最终达到一个稳定的速度，该速度下的重力和阻力相等，球体做匀速运动。我们在做数值仿真的时候，通常会因为网格的设置、物理场模型设置不合理等因素形成偏差，这需要结合具体的模型设置来判断，建议您将模型上传到COMSOL技术支持中心（https://cn.comsol.com/support），根据您模型的设置可以给出更有针对性的建议。
一帆 吴
2024-01-03我顶面给的压力出口 方管其余壁面全是无滑移璧，二维的时候速度增加到最大值就稳定了 三维增加后一直减小 都是一样的条件
一帆 吴
2024-03-10你好 我想问一下 我动网格自动重新划分几次后出现了网格反转，可以用反转之前也就是前一个时步的网格，用解的继承用这个网格接着算吗 不然每次从头开始算太花费时间了
Hao Li
2024-03-11 COMSOL 员工吴一帆，您好！
感谢您的评论。
可以的，在每个研究步骤的设置中可以选择变形构型的网格计算。
如果有进一步问题，建议您联系COMSOL的技术支持团队：
在线支持中心：cn.comsol.com/support
Email: support@comsol.com
谢谢！
诗翰 陈
2024-07-02您好 我想问一下要是我是把小球固定在一个上下运动的杆上呢，就是杆的上下运动带动球的运动，球和水面接触产生水波，研究水波的振幅这个时候该怎么建立模型啊
Yi Li
2024-07-08 COMSOL 员工思路和本案例基本一致，使用动网格描述杆和球的运动，使用两相流模型解析水波，如果有进一步问题，建议您联系COMSOL的技术支持团队cn.comsol.com/support， Email: support@comsol.com，谢谢。
迪 胡
2024-07-22您好，请问有水渗透过纱布的相关模型吗
Haoze Wang
2024-07-29 COMSOL 员工您好，暂无相关案例。建议您参考相似案例“纸条芯吸”：https://cn.comsol.com/model/wicking-in-a-paper-strip-79061
Zilong Li
2024-09-20您好，关于二维轴对称边界我有一些问题急需解决：我使用二维轴对称组件模拟一个充有液体的圆柱型封闭腔。流体是剪切增稠液，圆柱壳体是超弹性材料。由于壳体较软，我使用“流固耦合”，也就是双向流固耦合模块，对圆柱上表面进行准静态压缩。但是我的瞬态模拟都失败了，通过观察动网格，发现轴对称边界上，所有的流体网格的左边像被固定在轴对称边界上一样，随着压缩过程，最上方和上表面膜接触的一个流体单元网格最终都会被挤压至畸变。请问您知道这种情况该如何解决？
王 刚
2024-09-29 COMSOL 员工通常情况下，对称轴上的边界为“对称/辊支承”边界条件，从而可以在切向上运动。如果您的模型是这样设置，却出现所描述的现象，建议提交到 support@comsol.com 创建技术咨询工单。