从大型地质区域到纳米级结构,所有长度尺度上都会发生多孔材料中的流动。虽然许多应用都可以用达西定律来模拟,但是在工业应用中,速度场和压力梯度之间的关系不再是线性的,达西定律不能提供准确的结果。在这篇博客中,我们将更深入的研究多孔介质中可能出现的不同流动状态,以及如何描述它们。
在微观尺度上模拟多孔介质中的流动
为了深入理解多孔材料中的流动特征,我们有必要仔细研究它的微观结构。这不仅使我们能更深入的理解多孔材料,也有信心使用宏观方法来模拟多孔材料中的流动。
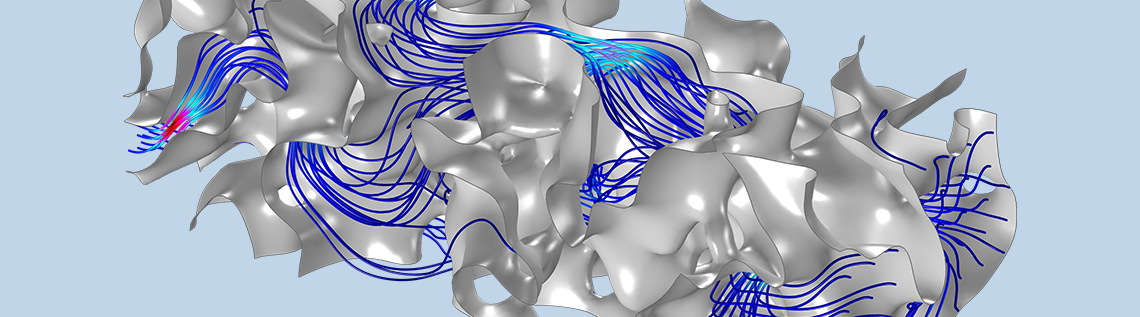
下面的动画显示了一个尺寸为 2 cm × 2 cm × 6 cm 的复杂多孔结构,以及使用线性纳维-斯托克斯方程计算的流型。
一个小的多孔块中的流型。
这个多孔块中有流速低的区域和流速高的区域,也有根本不发生流动的区域。即使多孔结构是不规则的,但当其被放大多孔,同一样本中的不同区域的流动特性是相同的。这种结构被称为 表征体元(REV)。采用表征体元的平均值可以得到一个宏观方程,详见下一节内容。
为了表征流动并获得有关宏观方程的信息,下面几个数值很重要:
- 孔隙率 \epsilon_p=\frac{V_\textrm{pore}}{V_\textrm{tot}},描述孔隙体积与总体积的比率,可以通过几何结构计算获得
- 沿流动方向(纵向)的压降 \Delta p/L,可以通过计算或预定义获得
- 表观速度 u=\frac{Q} {A},或通过结构的体积流率,由 Q (m3/s)除以总横截面积 A(m2 )获得。
宏观尺度上的流动
达西定律是描述多孔材料流动的基本方程,它最初只是一个经验定律,后来在理论上由纳维-斯托克斯方程推导出。它描述了速度场 \mathbf{u}(m/s)与压力梯度 p(Pa)之间的线性关系。
(1)
其中,\kappa(m2) 是多孔介质的渗透率, \mu (Pa·s) 是流体的动力黏度。
在如填充床或颗粒土等规则结构中,渗透性可以由 Kozeny-Carman 关系推导:
(2)
其中,d_\textrm{p} (m) 表示有效粒径(对于球形颗粒,它等于球体直径)。
线性达西定律适用于低速流动。与自由流动一样,多孔介质中的雷诺数
(3)
也用于表征流动,式中 L (m) 是特征长度尺度。
对于 Re<10,线性达西定律是有效的。因此 孔隙尺度流动可以被描述为蠕动流,其中惯性力比黏性力小得多。地下水流和其他低速和(或)高黏度流动的应用就是这种情况。然而,在大多数工业应用中,例如在填充床反应器、过滤器甚至食品工业中,都涉及到更高的流速,包括黏度非常低的气流。在这些应用中,仅使用 方程1 是无法描述的,还必须引入非线性项。这被称为非达西流,表述如下:
很明显,可以看到等式右侧的左边项对应于达西定律。至于非线性项,由 Forchheimer 方程可知,
(4)
其中,\beta 是惯性阻力系数,c_F 是 Forchheimer(无量纲)参数。
对于填充床应用,可以使用 Ergun 方程描述,使用以下关系式:
(5)
在高雷诺数下,黏性效应比惯性效应小,并且 Ergun 方程中的非线性项占主导地位,被称为 Burke-Plummer 方程。
这些方程已经可以很好地描述多孔介质中的非线性流动,但下面的图表会更便于观察。为了更好地观察,我们以平均粒径为 d_p=0.1 (mm) 的填充床中速度与压降的关系为例来说明。在下图中,Kozeny-Carman 描述了线性极限,Burke-Plummer 描述了二次极限。Ergun 和 Forchheimer 方程都可以描述线性和二次极限,两者之间的区别在于是根据 方程2 还是 方程5 计算渗透率的。
Kozeny-Carman、Forchheimer、Ergun 和 Burke-Plummer 关系的比较。
除上述考虑的情况之外,还有一种用于处理特殊气体流动的完全不同的非达西定律,即气体分子的平均自由程与孔隙尺寸大致相同的情况。在这种情况下,气体分子与孔壁的碰撞比与其他情况下气体分子的碰撞更频繁。这就是所谓的滑移流状态,从纳米材料到气体储藏模拟。其典型应用涉及范围很广。在这种情况下,渗透率方程为
(6)
其中,p_\textrm{A} 是绝对压力 (Pa) , \kappa_\infty 是高压下的渗透率 (m2),相较于分子之间的碰撞,分子与壁的碰撞与可以忽略不计。
Klinkenberg 参数 b_\textrm{K} (Pa) 取决于多孔介质的渗透率,可以在文献中查到 b_\textrm{K}
\propto\kappa_\infty^{-0.36}(参考文献 1)。
COMSOL 中的多孔介质流模块包含了上述所有渗透率模型。Forchheimer 和 Kozeny-Carman 方程在多孔介质流动的其他模块中也可以使用。
COMSOL 软件中渗透率关系的所在位置。
非达西流,从微观到宏观尺度
那么,如何将这两种方法联系起来呢?第一个模型,即表征体元,给出了速度与压力梯度的关系,也可以确定孔隙率和渗透率。同样,还可以观察不同数量级的压降流动行为。由于结构复杂,多孔结构模拟的计算成本相对较高,因此必须合理地求解。此外,与平均方程(方程2–方程 6)相比,纳维-斯托克斯方程本身就更为复杂。
使用宏观方法可以得到非常好的近似值。达西定律适用于小压降和低速流动,而 Burke–Plummer 方程适用于大压降和高速流动。
Forchheimer 方程可以很好地计算过渡区域。在本文的示例中,将 Forchheimer 方程与来自微观模型的数据相拟合,获得了 Forchheimer 参数 c_\textrm{F},该数据通常是通过实验确定的。
结束语
在这篇博客中,我们从微观和宏观层面研究了多孔介质中的流动,并演示了宏观方法可以得到非常好的近似值,并且有各自的适用领域。
多孔微通道散热器的优化案例模型就是使用 Forchheimer 方程模拟的一个工业应用示例。
在讨论了多孔介质中的流动之后,接下来我们将讨论多孔介质中的传热,敬请期待!
动手尝试
单击下面的按钮,进入 COMSOL 案例库,您可以下载 MPH 文件,尝试自己动手模拟文中介绍的案例模型。
参考文献
- Y. Wu, K. Pruess, and P. Persoff, “Gas Flow in Porous Media With Klinkenberg Effects“, Transport in Porous Media, vol. 32, pp. 117–137, 1998.
- J. Bear, Dynamics of Fluids in Porous Media, Courier Corporation, 1988.



评论 (6)
津杏 陈
2024-09-18请问如何在3d微观多孔介质内加入相场两相流动,同时涉及毛细压力?
Xiaohan Jiang
2024-09-20 COMSOL 员工您好,建议参考以下案例:https://cn.comsol.com/model/capillary-filling-1878。该案例所描述的就是液体在毛细力作用下的液面上升过程,可使用的接口包括水平集或相场。
紫芹 张
2024-11-07老师您好,如果我想要研究微米尺度弯曲膜孔内流体流动的数值模拟研究 ,对其初始速度和压强进行设置该如何进行呢,我在蠕动流文本下的初始值速度场进行调整几个速度绘制出来的速度图都是一样的,我不太明白问题出在哪里,请老师看到给我回个信,急需,感谢!
hao huang
2024-11-13 COMSOL 员工您好,可以保持默认初始值,但在边界条件处注意初值和边界条件不匹配的话会触发无法获取初始值的问题。关于设置了初始值却没有变化的问题,通常不会发生,需要查看具体的模型设置。
Ya Wang
2024-12-18老师,您好,我之前在技术邻网站(https://www.jishulink.com/post/318599)上看到关于耦合流动定律的简介,但是在官网上没有找到相关的说明,想了解有关Darcy-Brinkman模型与Navier-Stokes方程耦合的应用,麻烦老师帮我看看此模型是否是官方发布的教程,不胜感激!
Haoze Wang
2024-12-20 COMSOL 员工您好,目前最新版本的COMSOL(v6.3)中用于耦合多孔介质流和自由流动的接口为“自由和多孔介质流动,达西”和“自由和多孔介质流动,Brinkman”。您咨询的模型因发布时间早,现已不公开,请使用新版本中的接口进行建模。