模拟电磁波问题中的金属对象

金属是一种高导电材料，能够非常好地反射入射的电磁波—光、微波及无线电波。当通过 RF 模块和波动光学模块模拟频域电磁波问题时，您可以通过其中的几个选项来模拟金属对象。这里，我们将介绍阻抗、过渡边界条件和完美电导体边界条件，并说明每类条件何时使用。

什么是金属？

对于什么是金属这个问题，我们可以从用于求解电磁波问题的 Maxwell 控制方程组开始。考虑以下频域形式的 Maxwell 方程组：

上述方程通过 RF 模块和波动光学模块的电磁波，频域接口求解。方程求解了工作（角）频率 \omega = 2 \pi f 下的电场 \mathbf{E}。其他输入项包括以下材料属性：\mu_r 是 相对磁导率、\epsilon_r 是 相对介电常数，\sigma 是电导率。

出于本文的讨论目的，我们将假设集肤深度相对较小且有损耗的材料都是金属。有损耗材料指任何介电常数或磁导率为复数值、或电导率非零的材料。也就是说，有损耗材料会向控制方程引入一个虚数值项。这会在材料内产生电流，集肤深度是电流进入材料内深度的测量指标。

工作频率非零时，电磁感应都会将有损耗材料中的电流推向边界处。集肤深度是指电流减小到 63% 时进入材料的距离，可以通过以下公式计算：

其中 \mu_r 和 \epsilon_r 都可以是复数值。

在极高的频率（接近光学波段）下，材料接近等离子共振，我们实际上会通过复数值介电常数来表征金属。但当在低于这些频率下对金属进行模拟时，我们可以假设介电常数为一、磁导率为实数值，电导率非常高。因此上述方程可以简化为：

不过在您开始利用 COMSOL Multiphysics 进行模拟前，首先应计算或粗略估算所有模拟材料的集肤深度。集肤深度和零件尺寸信息，这两点将确定能否使用阻抗边界条件或过渡边界条件。

阻抗边界条件

既然已经知道了集肤深度，我们希望能将该值与模拟对象的特征尺寸 L_c 进行对比。L_c 有几种定义方式。根据具体情况，特征尺寸可以定义为体积与表面积的比值，或模拟对象最薄部分的厚度。

我们假设一个 L_c \gg \delta 的对象；也就是说，对象远大于集肤深度。虽然会有电流进入对象内部，但集肤效应会将这些电流推到表面上。因此，从模拟的角度来看，我们可以将电流看作在表面上方流动。此时就可以使用阻抗边界条件，它会将边界“背后”的所有材料处理为无限大。从电磁波的角度来看，这一点成立，因为 L_c \gg \delta 说明波不会穿透对象。

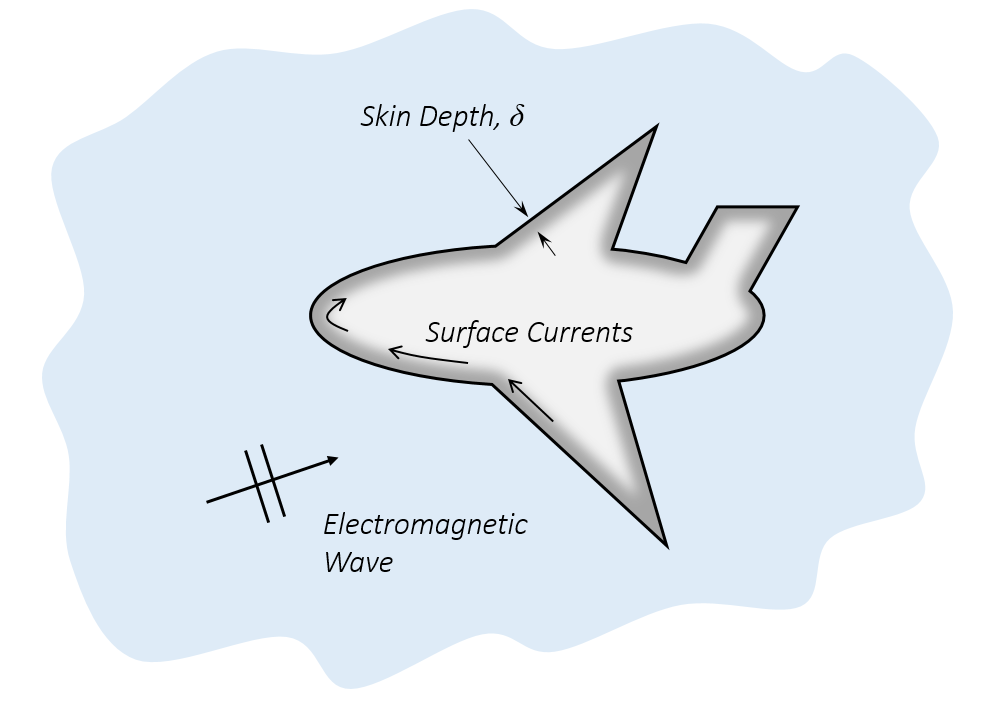
如果集肤深度远小于对象，就可以使用阻抗边界条件。

借助阻抗边界条件 (IBC)，我们可以假定电流完全在表面之上，因此不必再模拟模型金属域内任何部分的 Maxwell 方程组。所以，不必再对这些域的内部进行网格剖分，并能显著减少计算工作量。此外，IBC 还计算了由有限电导率造成的损耗。对于 IBC 适用情况以及与解析结果的对比，您可以查看腔体谐振器的 Q 因子和谐振频率教程案例。

随着 L_c / \delta \rightarrow \infty，IBC 将逐渐更精确；对于类似球体的光滑对象，即使 L_c / \delta \gt > 10 ，它仍能保持精确。对于类似楔形的锋利对象，拐角处会略微不精确，不过正如 “通过圆角消除电磁场的奇异性” 博客中的讨论，这属于局部影响，也是向模拟引入尖角后的一个固有问题。

现在，如果我们要处理类似铝箔这种一个维度远小于其他维度的对象呢？此时，一个方向上的集肤深度可能会与厚度相当，因此电磁场将部分穿透材料。此时就不再适合使用 IBC，我们将使用过渡边界条件。

过渡边界条件

过渡边界条件 (TBC) 适用于模拟对象的厚度与特征尺寸和曲率相比较小的导电材料层。即使厚度是集肤深度的数倍，还是可以使用 TBC。

TBC 会将材料属性及膜厚度作为输入项，并通过膜厚度及切向阻抗来计算阻抗。这些可以用于将膜两侧表面的电流关联起来。也就是说，TBC 会造成所传输电场的下降。

从计算的角度来看，为了计算 TBC 两侧的电场，边界处的自由度数将增加一倍，如下图所示。此外，还将计算通过膜厚度的总损耗。有关该边界条件使用的示例，您可以查看分光器教程案例，它利用一个复数值介电常数模拟了银薄层。

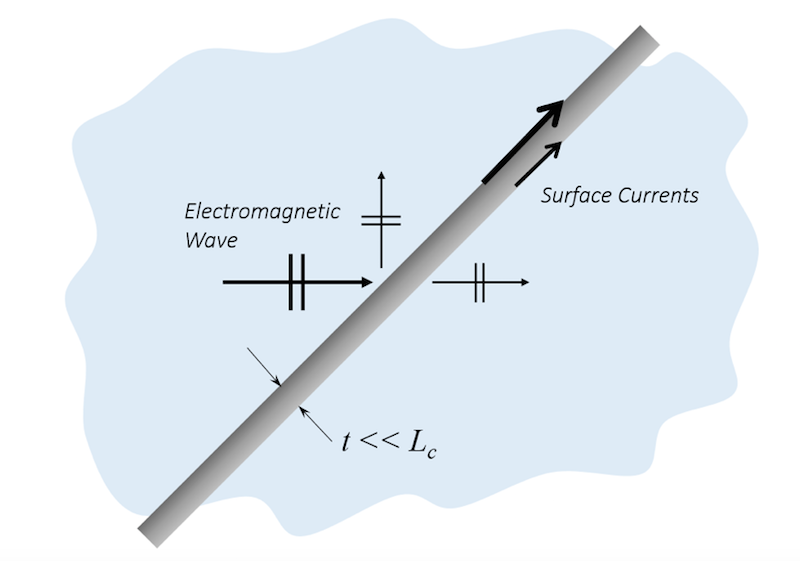
过渡边界条件会计算边界两侧的表面电流。

增加表面粗糙度

截至目前，TBC 和 IBC 都假定表面是完美的。我们一般认为平面边界在几何上是完美的。正如 “线性静态问题的网格剖分注意事项” 博客中的介绍，弯曲边界可以在所用有限元网格的精度内被解析，即几何的离散误差。

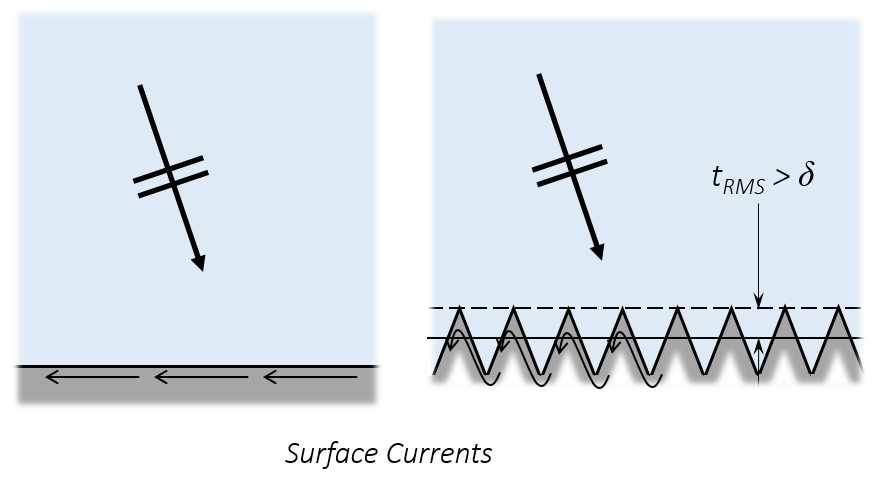
与平滑表面相比，粗糙表面会阻碍电流。

但所有真实表面都存在一定的粗糙度，而且可能很大。表面的不完美将影响电流的纯切向流动，并会有效降低表面电导率（如上图所示）。在 COMSOL Multiphysics 5.1 版本中，我们可以通过向 IBC 和 TBC 条件增加表面粗糙度特征来分析该影响。

对于 IBC，输入是表面高度粗糙度的均方根 (RMS)。对于 TBC，输入为膜厚度变化的均方根。粗糙度的幅值应大于集肤深度，并远小于零件的特征尺寸。表面的等效电导率会随粗糙度的升高而降低，如 E. Hammerstad 和 O. Jensen 在 “微带线计算机辅助设计的精确模型” 论文中的介绍。雪球模型是第二个粗糙度模型，用到了 P. G. Huray 在“信号完整性基础” 中提到的关系式。

完美电导体边界条件

我们还应该再分析一种理想化的情况 — 完美电导体 (PEC) 边界条件。对于无线电和微波领域的许多应用而言，金属边界处的损耗要远小于系统内的其他损耗。例如在微波电路中，电介质基板处的损耗通常远大于任何金属喷镀处的损耗。

PEC 边界是一种无损耗表面；能够 100% 反射入射波。该边界条件可以满足许多模拟需求，可以用在模型开发的早期阶段。有时，查看您的设备在零材料损耗下的表现也会很有意思。

此外，您可以将 PEC 边界条件作为对称条件使用，简化您的模拟。根据对场的预先判断，您可以使用 PEC 边界条件以及其补充，完美磁导体 (PMC) 边界条件，来使电场强制对称。计算完美导体球的雷达截面教程案例介绍了如何将 PEC 和 PMC 边界条件作为对称条件使用。

最后，COMSOL Multiphysics 中还包括表面电流、磁场和电场边界条件。提供这些条件主要是考虑数学上的完整性，因为我们永远也无法事先得知表面上的电流和电场。

小结

在本篇博客中，我们重点介绍了如何借助阻抗、过渡及完美电导体边界条件来模拟金属表面，并说明了每种边界的应用场景。不过，如果您无法使用其中任意一种边界条件呢？或者您模拟零件的特征尺寸与集肤深度类似？此时，您将不能再使用边界条件；您需要显式模拟金属域，类似于对其他所有材料的处理。这是该系列的下一个主题，请继续关注。