在很多情况下,我们可能会对模拟周期性（即使非正弦的）电信号感兴趣，目的是计算由此产生的电场、热损耗和温度变化。例如，电脉冲列可以被施加到人体组织中进行神经调控、电穿孔或热消融等。虽然我们可以通过时域仿真来模拟这类信号，但是也可以通过傅立叶变换方法来高效计算线性响应。接下来，让我们了解更多内容！
目录
简介
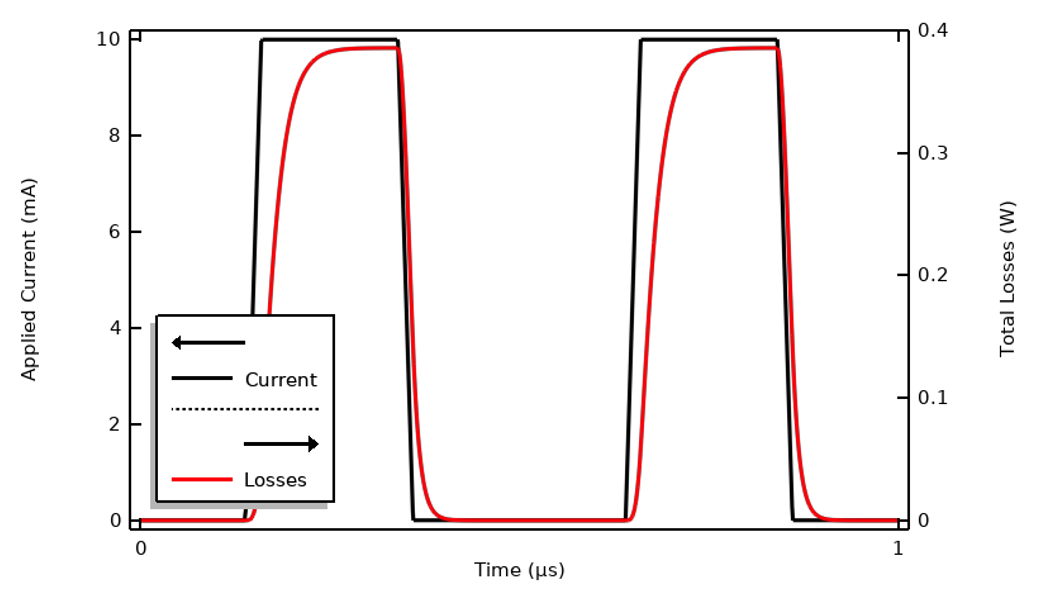
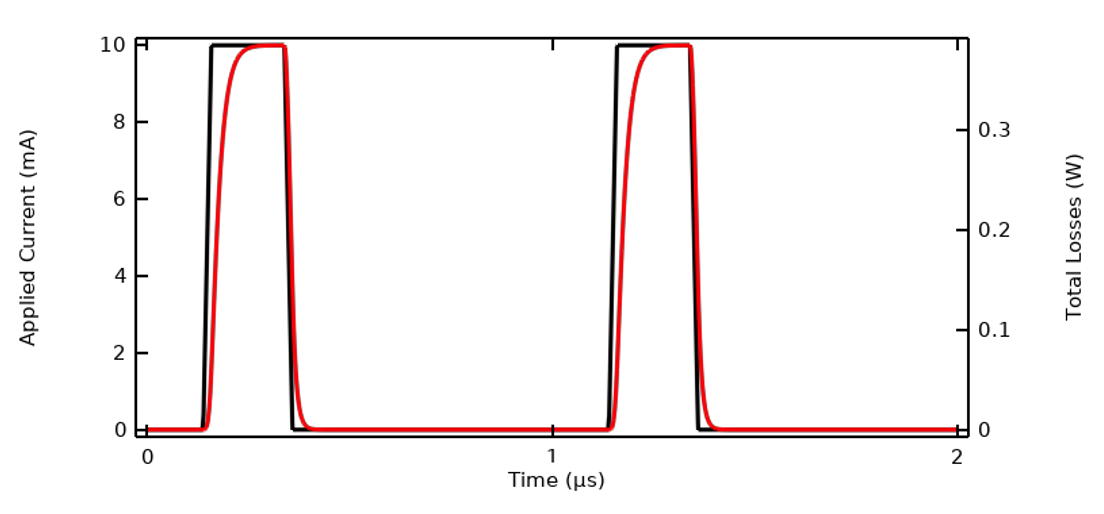
我们将继续使用上一篇博客：理解瞬态电磁激励选项中使用的示例模型，并使用 电流 接口来求解。我们在上一篇博客中重点介绍了这个接口，并证明了它足以求解此类模型。以一个电流激励周期为 1µs 的梯形脉冲波形模型为例来说明。该模型可在时域中求解，终端电压和总损耗如下所示。
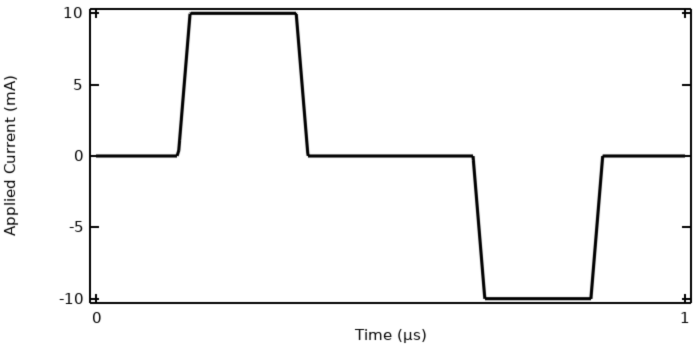
向模型施加的电流为梯形脉冲波。
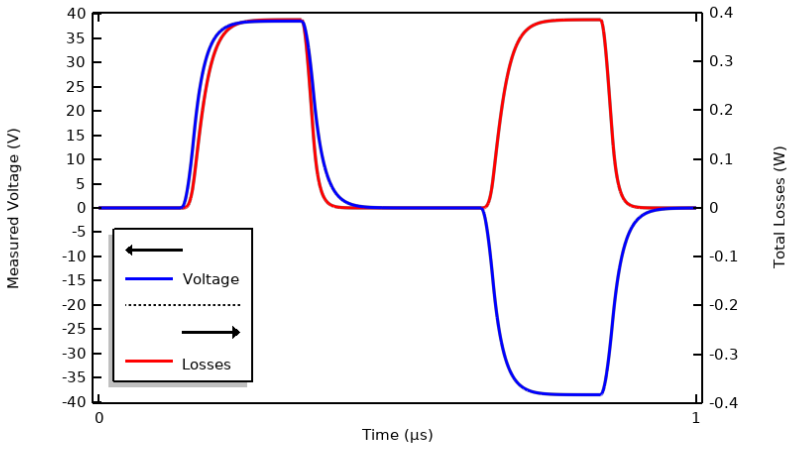
计算的一个周期内的终端电压和材料损耗。
我们还可以对此模型进行扩展，求解温度并使电导率成为温度的函数，从而将其转化为双向耦合的多物理场模型。我们将使用以下表达式：\sigma (T) = 0.03\exp \left(-\frac{T-20^\circ \text{C}}{20\text{K}}\right) \text{S/m}。
建模域的侧边和底部采用了固定的温度边界条件。在一个时间段（1µs）内求解模型，可以检查该时间段内的温度变化。如下图所示，温度变化很小。
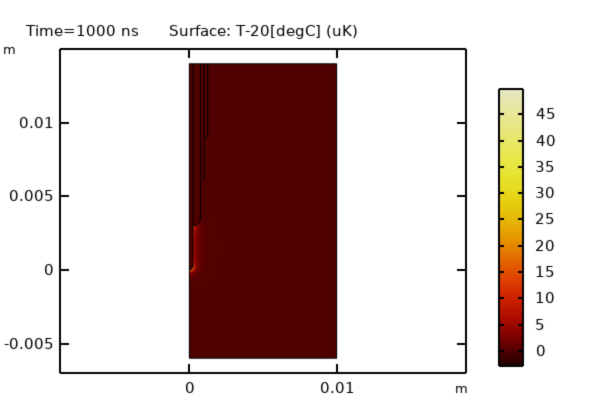
1µs 后的温度变化很小。
然而，我们需要求解的温度变化时间要比一个周期长得多，因此这种模拟方法的计算成本太高。我们需要寻找其他方法。不过，在此之前，我们需要对这个模型和结果做一些说明：
- 外加电流围绕周期平均值零变化，因此输入信号没有直流分量。
- 计算得出的终端电压和损耗在脉冲之间归零。
- 电导率和相对介电常数都不直接取决于电场。
- 终端电压滞后于电流，说明系统具有很大的电容。
- 在一个激励周期内，温度上升的幅度非常小。
由于观察到温升在与电激励周期相似的时间跨度内非常小，我们可以将电问题看作时间上的局部线性问题。我们可以通过对外加信号进行傅立叶变换，然后求解频域模型，并使用逆傅立叶变换来重建电气模型的瞬态结果，从而重现结果。这样，我们很快就能了解到输入信号中哪些谐波对发热有重大影响。
我们可以使用双向耦合模型求解时间跨度比激励周期长得多的瞬态温度变化问题，该模型在求解温度场问题的同时，还求解了多个电流 接口问题，输入信号的每个重要频率分量都有一个电流接口。这样做能大大提高计算效率。COMSOL 学习中心文章：了解周期信号及其频率组成、使用逆快速傅立叶变换重建瞬态信号和设置和求解电磁热问题介绍了这种模拟方法的几个步骤。接下来，我们将对这些步骤进行总结。
了解输入信号的频率组成
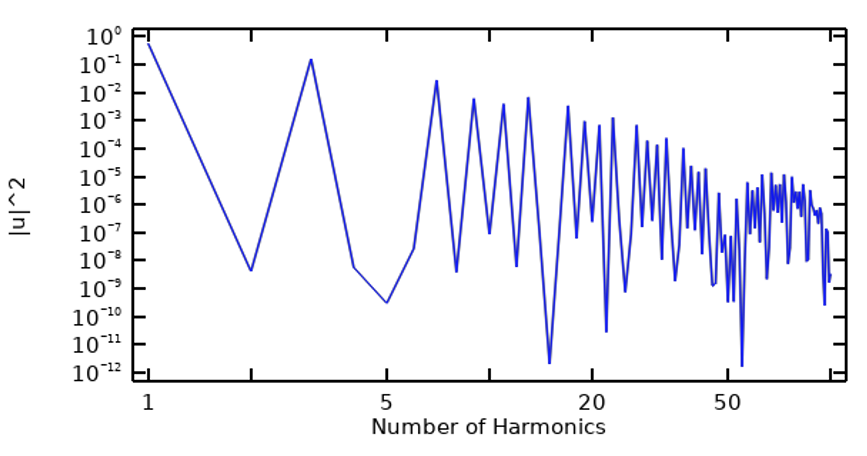
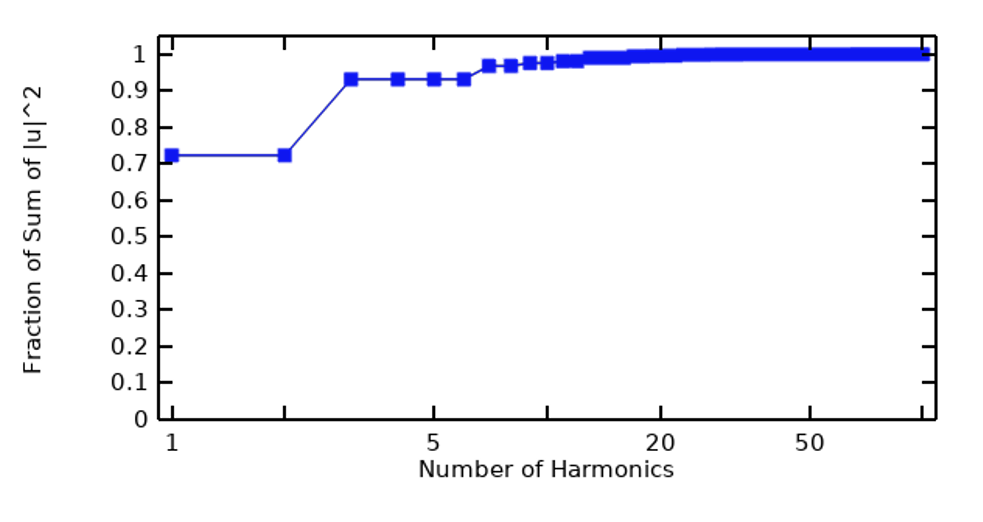
从周期信号开始，我们可以对信号进行快速傅立叶变换，来检查其频率组成，这可以通过各次谐波的幅度以及当前谐波之前的累积总和来实现。在下图中，左边的图像是梯形脉冲波的频率组成，右边的图像是累积总和。
梯形脉冲波的频率组成（左）和累积总和（右）。
通过这个初始步骤，我们可以看到，至少在这个例子中，只有数量相对较少的谐波贡献了信号中的大部分能量，某些谐波的贡献可以忽略不计。
在频域中求解
除了施加信号的快速傅立叶变换，我们还需要使用一个在所有频率幅值内相同的激励，来计算系统对频域激励的响应。请注意，这并不代表系统在所有频率上的响应都是相同的，我们在博客：理解电流建模的激励选项中对此进行了深入探讨。下图所示为在一定频率范围内扫描的结果，即周期平均损耗图。从图中可以推断出，我们正在使用的模型具有随频率显著变化的阻抗。在这种情况下，我们将求解前 100 次谐波，只要知道哪些频率重要，就可以运行一组较小的频率。
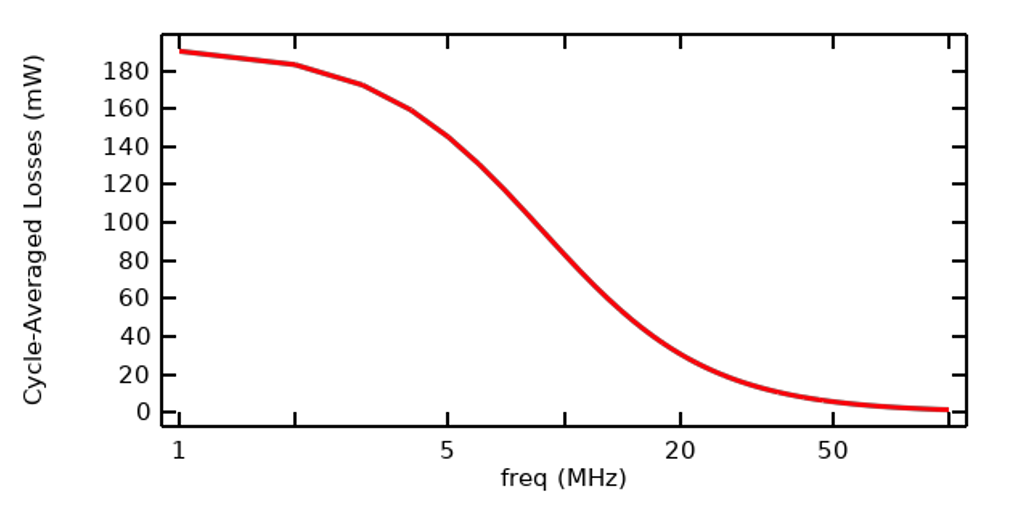
在所有频率下使用等效激励，样本中的周期平均损耗与频率的函数关系图。
重建瞬态结果
由于我们已经有了输入信号的快速傅立叶变换，只要计算出频域结果，并对所有考虑的频率进行单位激励，就可以使用逆快速傅立叶变换 (IFFT) 重建系统的瞬态响应。下图的结果显示了逆快速傅立叶变换的计算结果与瞬态计算结果吻合的很好，而且逆快速傅立叶变换方法的计算量较小。
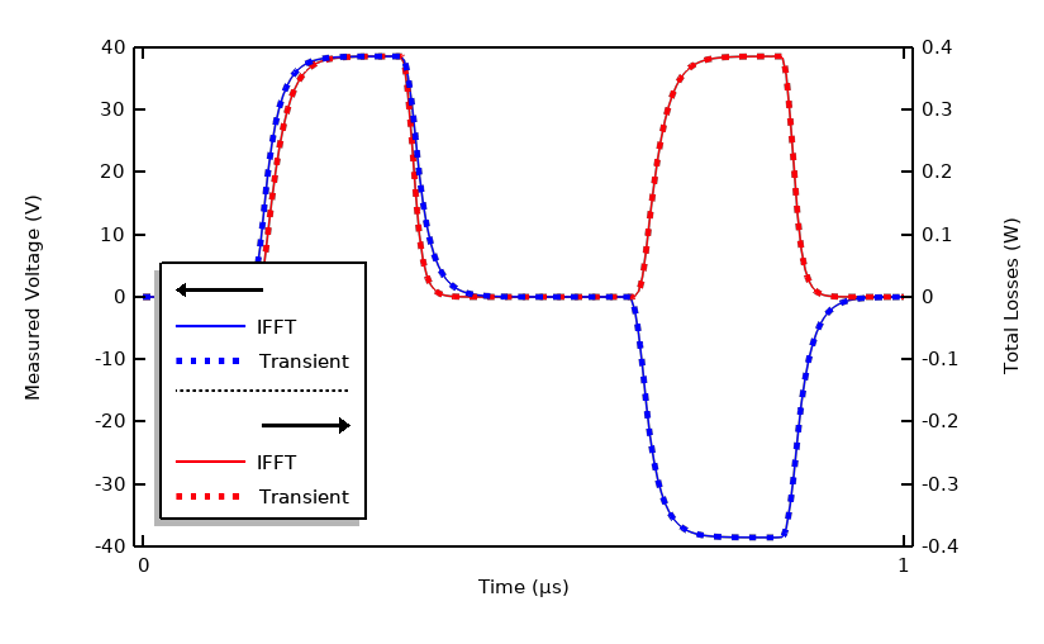
瞬态结果与使用 100 次谐波的逆快速傅立叶变换重建系统的计算结果的比较。
虽然在瞬态结果具有极好的一致性非常有用，但我们通常只对加热感兴趣，因此与其根据时域的一致性来计算逆快速傅立叶变换结果，还不如比较一个周期内的时间积分损耗。对于这个施加的信号，只需求解 1 次、3 次、7 次和 9 次谐波，就能模拟 99% 的损耗。也就是说，尽管瞬态结果明显不同，但总的积分损耗结果却相当吻合。
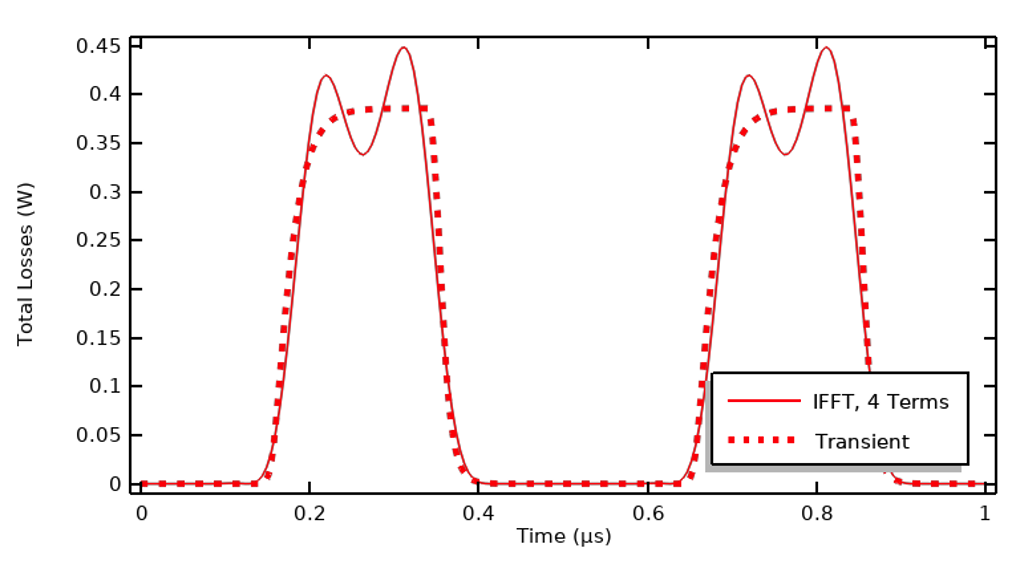
时域损耗与仅使用 4 次谐波通过逆快速傅立叶变换重建系统计算的损耗比较。
在上图中，我们可以看到，虽然瞬态结果的一致性看起来不是那么好，但整个时间段内积分损耗的一致性小于 1%。
使用快速傅立叶变换结果进行热分析
到目前为止，我们已经研究了如何重建单个周期内的瞬态损耗变化，但出于热分析的目的，我们可能会对更长的模拟时间感兴趣，因为温度变化的时间跨度要比电信号的时间跨度长很多倍。如果材料的电导率随温度变化，就需要在模型中加入物理场的双向耦合。如果尝试同时求解电场和温度场，并采用足够精细的时间分辨率来模拟电激励，那么最终会得到一个需要很长时间才能求解的模型。虽然有时这样做是合理的，但我们往往需要一种更快的方法，而这正是我们迄今为止计算出的数据发挥作用的地方。
如下图所示，根据前几次谐波的贡献总和，可以将时域损耗近似为时间上的均匀损耗。在热时间尺度远长于电时间尺度的假设条件下，这种方法是有效的。
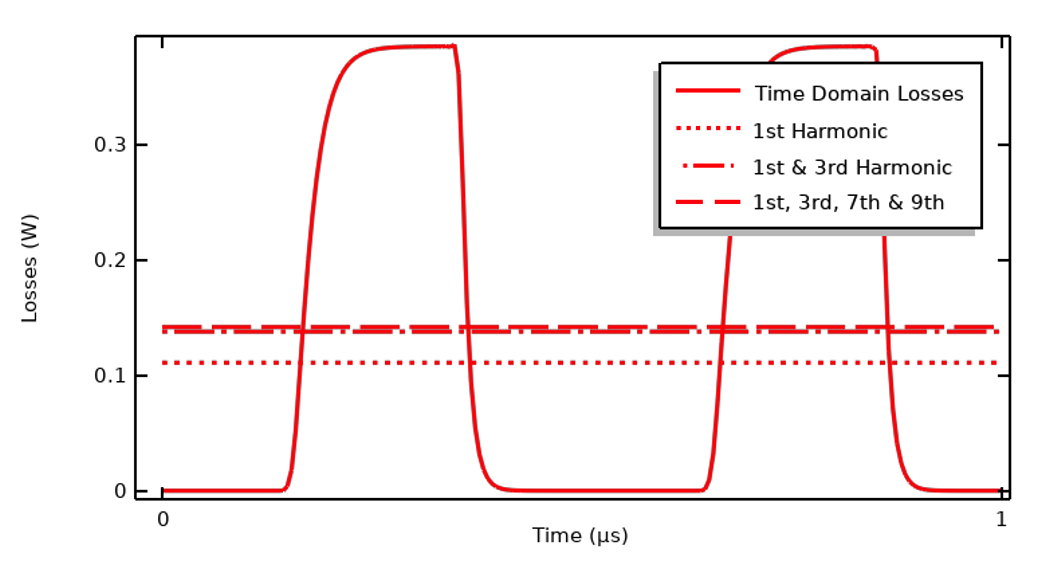
比较时域损耗与几个谐波计算的周期平均值之和的曲线图。
正如我们之前所观察到的，对于该输入信号，我们只需要基波、3 次谐波、7 次谐波和 9 次谐波就可以捕获到一个周期内 99% 的热现象。这意味着我们可以建立一个新模型，其中包含四个不同的电流 物理场接口，每个接口在频域中针对不同的谐波求解，并将每个谐波的外加电流大小乘以输入信号的相应傅立叶系数。然后，这些接口可与瞬态（或稳态）热模型一起求解，后者将计算温度变化，并纳入双向耦合，因为电材料特性是温度的函数。这种方法的计算效率相对要高得多，而且可以建立三维几何模型。有关如何建立这类模型（输入信号的快速傅立叶变换结果用于定义热载荷）的指南，请参阅 COMSOL 学习中心的文章：设置和求解电磁热问题。
利用外加电流波形谐波总和引起的周期平均加热，在三维模型中计算出的温度升高。
改变脉冲类型和间距
如果要模拟脉冲序列，即严格意义上的正信号，会发生什么情况也值得探讨。这种信号有直流分量，理论上会使逆快速傅立叶变换的工作变得更加复杂，因为还需要考虑稳态解。但由于我们只关心加热，而且如果在脉冲之间损耗降为零，那么激励的符号并不重要。也就是说，无论电流流向如何，电热都是一样的。如果随着时间的推移，脉冲之间的热降至零，那么在逆快速傅立叶变换中就不需要考虑热的直流分量。因此，即使在处理严格意义上的正输入信号时，也可以将其视为正负转换信号，这样做只是为了简化逆快速傅立叶变换重建系统。下图中的信号和前面介绍的信号在计算损耗方面是相同的。
与对称信号相比，严格为正的输入信号会产生相同的热，只要热曲线在两者之间归零即可。
我们还可以改变脉冲之间的间距，从而增加输入信号的周期，因此我们可能会认为需要重新进行快速傅立叶变换。然而，由于在原始信号中，脉冲之间的热降为零，因此增加热为零的时间并不会改变单脉冲造成的损耗。也就是说，如果我们有一个脉冲间距时间较长的脉冲序列，只需对脉冲间距时间较短的信号进行快速傅立叶变换即可，因为这足以准确预测热曲线了，而且还能节省计算量。在求解双向耦合热问题时，外加信号必须按占空比平方根的系数进行缩放。在下图中，脉冲持续时间相同，但周期加倍，因此占空比为 0.5。
增加脉冲间距时间不会改变每个脉冲的热曲线。
忽略电容效应，进一步简化分析
到目前为止，我们所考虑的示例设计（就材料特性和波形而言）是为了说明快速傅立叶变换方法最有用的案例。这种复杂程度并非总是需要的。回到第一次绘制的外加电流和终端电压图，用不同的样本材料（导电率是原来的10倍）重新绘制，结果将与下图类似。相对于周期，电压和电流之间的滞后可以忽略不计，这意味着几乎不存在电容效应。或者说，系统阻抗几乎是纯电阻性的，并且在相关频率范围内保持不变。同样，如果使用相同的波形，但速度慢十倍，响应也会相似。
将电导率提高 10 倍将改变系统的响应。电容效应现在可以忽略不计。
假设我们处理的是一个几乎纯电阻系统，并假设电导率相对于外加信号的频率组成是恒定的，那么就有可能将电气模型简化为一个稳态直流问题，从而完全忽略电容效应和由此产生的位移电流。这样，电流 物理场接口就能以稳态 形式求解，而外加直流信号就是瞬态信号平方的周期平均值的平方根：
无论激励是以电流、电压还是终端电压表示，这个表达式都是相同的。只要电气特性相对于频率和电场强度是恒定的，使用这种简化方法是有效的。
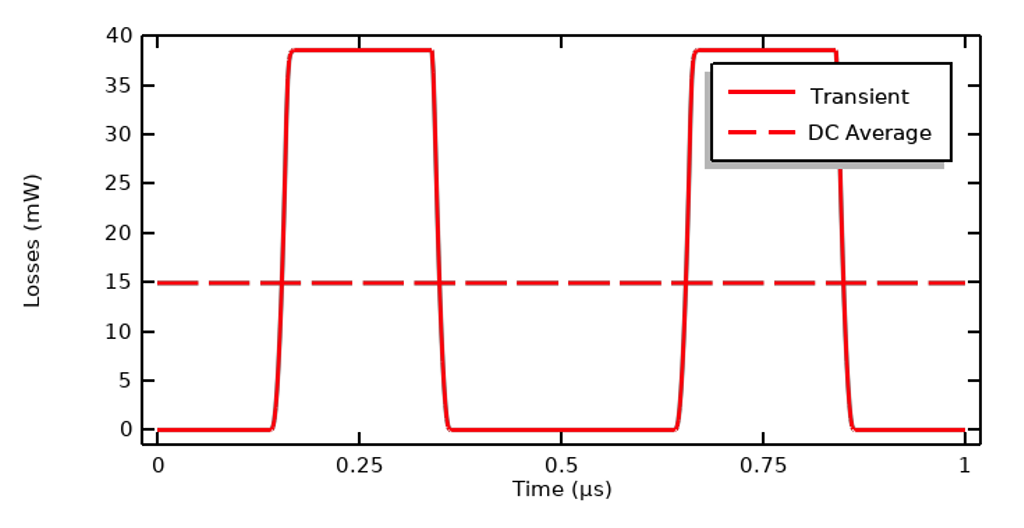
近乎纯电阻材料的时域损耗和直流等效平均值。
结束语
在这篇博客中，我们研究了如何建立周期性电激励模型，以及如何将其简化为单个周期。通过对输入信号进行快速傅立叶变换，可以确定重要的频率组成，通过求解一系列频率和逆快速傅立叶变换研究步骤可以预测瞬态系统响应。
快速傅立叶变换和逆快速傅立叶变换的结果可用于预测随时间变化的响应，并可用作电热仿真的输入。将周期信号近似为若干次谐波之和的方法尤其有效，这样我们就可以将其作为双向耦合的多物理场问题进行高效处理。对于某些类型的问题，我们可以通过完全忽略频率组成来进一步简化。
如果您的仿真涉及这方面的内容，那么在建立多物理场模型时，需要充分了解所有这些复杂性和简化性。
评论 (0)