
每次利用 COMSOL Multiphysics 求解电磁波问题时,我们都会开发一个包含多个域和边界条件的模型,并且在域内使用各种材料模型来表征不同物质。从数学的角度来看,所有这些材料最终都会在控制方程内以相同的方式进行处理。让我们来分析这些材料模型,讨论何时应使用这些模型。
我们在求解哪些方程组?
博客将介绍电磁波,频域接口内使用的频域形式 Maxwell 方程组,您可以在 RF 模块和波动光学模块找到这个接口。博客内容也适用于波动光学模块的电磁波,波束包络公式。
假设材料响应与场强线性相关,我们将能在频域写出 Maxwell 方程组,因此控制方程将能写为:
此方程求解了工作(角)频率 \omega = 2 \pi f 下的电场 \mathbf{E},其中 c_0 是真空中的光速。其他输入项包括以下材料属性:\mu_r 相对磁导率、\epsilon_r 相对介电常数和 \sigma 电导率。所有这些材料输入可以是正值或负值、实值数或复值数,还可以是标量或张量。材料属性可以随频率变化,不过如果我们只需分析一个相对较窄的频率范围,那一般不需要考虑该变化。
我们接下来将详细分析每一种材料属性。
电导率
电导率量化了材料的导电能力,是电阻率的导数。 我们通常在稳态 (DC) 下测量材料电导率,从以上方程可以看出,材料的等效电阻率将随频率的升高而增大。我们通常假定电导率与频率一致,不过我们稍后将讨论几个材料电导率会随频率变化的模型。
如果材料的电导率非零,当向材料施加电场后,它将开始传导电流并会因电阻损耗而耗散能量,即焦耳热。此时,温度会上升,并导致电导率发生改变。您可以输入任意函数或列表数据来表示电导率随温度的变化,也可以使用软件内置的线性电阻率模型。
线性电阻率模型常用于模拟电阻率随温度的变化,公式为:
其中 \rho_0 指参考电阻率、T_{ref} 指参考温度,\alpha 是电阻温度系数。您可以指定或通过计算得到随空间变化的温度场 T。
电导率作为实值数输入,而且它也可以具有各向异性,即材料电导率会在不同的坐标方向发生变化。例如在层压材料中,如果您不希望显式模拟单独的每一层,那就可以使用此方法。您可以为复合材料输入一个经实验确定或在单独的分析中计算得到的均匀电导率。
RF 模块还提供了其他两个选项来计算均匀电导率:Archie 定律(用于计算充满导电流体的不导电多孔介质的等效电导率)和混合了多种材料的多孔介质模型。
Archie 定律模型常用于模拟饱含海水、原油或其他电导率要高于土壤的流体的土壤。
多孔介质模型提供了三个选项来计算混合材料(最多包含五种材料)的等效电导率。 首先是体积平均电导率,公式为:
\sum \theta_i \sigma_i
其中,\theta 是每种材料的体积分数。模型适用于各种材料的电导率相似的情况。如果电导率的差别很大,那更适合使用体积平均电阻率:
\sum\frac{\theta_i}{ \sigma_i}
最后,幂律公式给出的电导率介于其他两个公式之间:
\prod\sigma_i^{\theta_i }
这些模型只适用于材料属性变化的长度量级小于波长的情况。
相对介电常数
相对介电常数量化了当向材料施加电场后材料的极化程度。通常我们可以称所有 \epsilon_r>1 的材料为介电材料,即便真空 (\epsilon_r=1) 也可以被称作电介质。我们还经常使用介电常数来描述材料的相对介电常数。
材料的相对介电常数通常是复值数,其中负的虚部表示当电场方向随时间改变时,材料中的损耗。当材料中的电场随时间改变时,材料会以热的形式耗散部分电能。此时,原子周围电子云的形状随电场改变,产生了这种我们称为介电损耗的现象。介电损耗的概念不同于之前讨论的电阻损耗;但它们的数学处理完全相同,都是作为控制方程中的一个复数值项进行处理。请记住 COMSOL Multiphysics 遵循了以下惯例:负的虚部(正的电导率值)将造成损耗,而正的复值组分(负的电导率值)将在材料中产生增益。
软件提供了七个相对介电常数模型;我们接下来将具体介绍这些模型。
相对介电常数是 RF 模块的缺省选项,可以输入实值或复值标量或张量。电导率部分提到的多孔介质模型同样适用于相对介电常数。
折射率是波动光学模块的缺省选项。您可以单独输入折射率的实部和虚部,即 n 和 k,同时相对介电常数是 \epsilon_r=(n-jk)^2。该材料模型假定电导率为零,并假定了单位相对磁导率。
损耗角正切需要输入实值相对介电常数 \epsilon_r'和标量损耗角正切 \delta。相对介电常数由 \epsilon_r=\epsilon_r'(1-j \tan \delta) 计算,且材料电导率为零。
通过介电损耗选项可以输入相对介电常数 \epsilon_r=\epsilon_r'-j \epsilon_r'' 的实部和虚部。 请注意符号:使用该接口时,如在虚部 \epsilon_r'' 输入一个正的实值数,将造成损耗,因为软件内部会将其乘以 -j。您可以浏览金纳米球的光散射模型示例,学习该材料模型的使用。
Drude-Lorentz 弥散是基于 Drude 自由电子模型和 Lorentz 振荡模型开发的材料模型。Drude 模型 (\omega_0=0) 用于金属和掺杂半导体,Lorentz 模型描述了声子模及带间跃迁等谐振现象。通过加和来结合这两个模型,将能精确描述各类固体材料。它预测了复相对介电常数随频率的变化:
\sum\frac{f_k\omega_p^2}{\omega_{0k}^2-\omega^2+i\Gamma_k \omega}
其中 \epsilon_{\infty} 是对相对介电常数的高频贡献、\omega_p 是等离子体频率、f_k 是振荡器强度、\omega_{0k} 是谐振频率,\Gamma_k 是阻尼系数。由于模型计算了复值介电常数,COMSOL Multiphysics 内的电导率将设为零。这是模拟依赖于频率的电导率的方法之一。
Debye 弥散模型是 Peter Debye 基于极化弛豫时间开发的材料模型。模型主要用于极性液体。它预测了复相对介电常数随频率的变化:
\sum\frac{\Delta \epsilon_k}{1+i\omega \tau_k}
其中 \epsilon_{\infty} 是对相对介电常数的高频贡献、\Delta \epsilon_k 是对相对介电常数的贡献、\tau_k 是弛豫时间。由于模型计算了复值介电常数,电导率假定为零。这是另一种模拟依赖于频率的电导率的方法。
波动光学模块中的 Sellmeier 弥散模型主要用于光学材料。它假定电导率为零、单位相对磁导率,并基于工作波长 \lambda 而非频率定义了相对介电常数:
\sum\frac{B_k \lambda^2}{\lambda^2-C_k}
其中系数 B_k 和 C_k 确定了相对介电常数。
您可以根据技术文献给出的材料属性在这七个模型中进行选择。请记住,从数学角度来看,它们在控制方程中的输入方式相同。
相对磁导率
相对磁导率量化了材料对磁场的响应。我们将所有 \mu_r>1 的材料称为磁性材料。铁是地球上最常见的磁性材料,但我们很少在 RF 或光学应用中使用高纯铁,更常使用的是铁磁性材料。这类材料会表现出强烈的各向异性磁属性,可以通过施加 DC 磁场控制。与铁不同,铁磁性材料的电导率较低,因此高频电磁场能够透入材料并与材料主体发生相互作用。参数化环形器结构教程演示了如何模拟铁磁性材料。
可以通过两个选项指定相对磁导率:相对磁导率模型(RF 模块的缺省选项)和磁损耗模型。相对磁导率模型支持您输入一个实值或复值标量或张量。电导率部分提到的多孔介质模型同样适用于相对磁导率。与上文提到的介电损耗模型类似,磁损耗模型中相对磁导率的实部和虚部可以作为实值数输入,虚数磁导率将在材料中造成磁损耗。
模拟与网格剖分注意事项
在所有电磁模拟中,我们都不应忽视集肤深度这个重要的概念,即材料中的电场减小到表层电场值的 1/e 的距离。集肤深度可以定义为:
我们可以看到相对介电常数和磁导率均为复值。
您应始终检查集肤深度,并与您模型域的特征尺寸进行对比。如果集肤深度远小于对象,您可以按照 “模拟电磁波问题中的金属对象” 博客中的做法将域作为一个边界条件模拟。如果集肤深度与对象尺寸相仿或更大,电磁场将透入对象并在域内发生明显的相互作用。
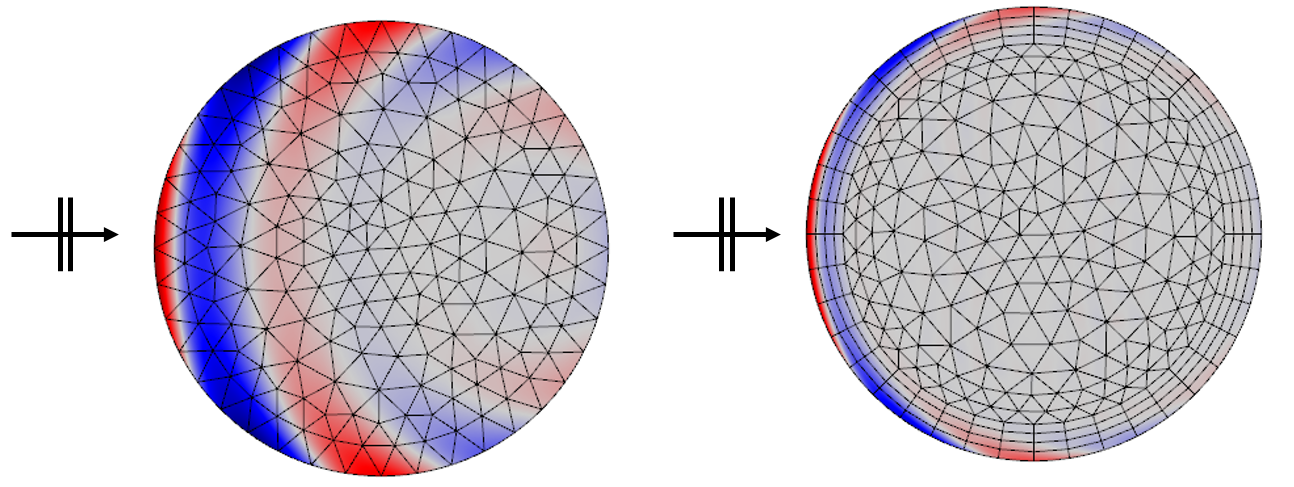
入射在电导率及集肤深度不同的对象上的平面波。集肤深度小于波长时,使用边界层网格(右)。绘制了电场。
如果集肤深度小于对象,那建议使用边界层网格剖分来求解边界法向方向上的场中的强烈变化,每单位集肤深度应至少使用一个单元,同时应使用至少三个边界层单元。如果集肤深度大于介质的等效波长,那就可以通过在每波长应用五个单元来求解介质本身的波长,如上方左图所示。
小结
在本篇博客中,我们介绍了 COMSOL Multiphysics 中用于定义电磁波模型中材料属性的几种方法。我们发现在特定频率范围内,用于定义相对介电常数的材料模型也可以用于金属材料。另一方面,根据 “模拟电磁波问题中的金属对象” 博客中的介绍,我们还可以通过边界条件定义金属域。结合我们之前发布的关于模拟开放边界条件及关于模拟端口的博客,我们已经基本掌握了电磁波模拟的所有相关基础知识。不过,我们还有一些要点尚未涉及,请继续保持关注!



评论 (0)