武士刀（katana）是几个世纪前的日本武士使用的一种兵器，弯曲的形状和锋利的单刃是其典型特征。这篇博客，我们将讨论如何使用 COMSOL Multiphysics® 软件建立一个简单的武士刀模型，并通过模拟局部淬火过程来探讨其特性。
内容简介
著名的武士刀
很少有武器能像日本武士（samurai）的随身武器——武士刀一样闻名于世。武士刀以锋利著称，只有在最后关头才会出鞘，武士刀及其与主人之间近乎神圣的联系激发了多部现代电影、电视剧和书籍的创作灵感。在电影《杀死比尔 I》（Kill Bill I，2003）和《杀死比尔 II》（Kill Bill II，2004）中，Uma Thurman 扮演的“新娘”在现代东京挥舞着武士刀；在 James Clavell 的经典小说《幕府将军》（Shogun，1975）中，James Blackthorne 船长被吹到日本海岸，并被日本武士俘虏。
一名日本武士，照片由摄影师 Felice Beato 拍摄于 1860 年。这张照片在美国属于公有领域，它在日本的版权于 1970 年到期，而且 Uruguay Round Agreements Act 也没有恢复其版权。来源：Britannica。
当然，武士刀的大部分恶名是因其使用者而获得的。但是，日本刀匠是如何为日本武士打造这些武器的呢？他们是如何在刀刃的软硬之间实现微妙的平衡，使武士刀既锋利无比，又有足够的韧性来承受反复的冲击？为什么武士刀的刀刃是弯曲的，而不是笔直的？这篇文章，我们将介绍如何模拟武士刀的局部硬化过程，并研究其中包括的物理效应，来看看能否对这一历史上著名的武器制作过程有所了解。
金属加工模块
金属加工模块是 COMSOL Multiphysics® 的一个附加产品，可用于模拟如钢铁等铁合金和 Ti-6Al-4V 等钛合金的相变，以及钢淬火和增材制造等应用。例如，钢淬火可用于汽车变速箱部件的淬火仿真，增材制造则涉及打印过程中出现的反复冷却-加热循环。耦合了固体力学和传热的相变仿真，能够模拟塑性和相变潜热等效应。
局部硬化
大多数情况下，仅需要对组件的部分区域进行淬火。例如，感应淬火就是这样一种工艺。它通过线圈施加强交变磁场，从而在组件表面产生感应电流。然后对组件进行淬火，使组件表面区域发生马氏体转变。这种局部淬火工艺通常用于车轴和齿轮等传动组件，以提高耐磨性和抗疲劳性。
火焰淬火是另一种可用于获得组件硬表面的工艺。这种工艺不使用交变磁场，而是通过将气体火焰施加在组件表面进行局部加热，然后进行淬火处理。
当然，感应淬火和火焰淬火是相对新颖的热处理工艺，数世纪以前的日本刀匠根本无法使用。制作传统的日本武士刀使用的是另一种局部淬火工艺。对于武士刀这种类型的兵器来说，最好的状态是刀刃锋利且边缘坚硬（理想情况下是纯马氏体），同时剑脊最好具有韧性，例如珠光体，否则可能会在受到冲击时断裂。对武士刀进行不同程度的局部硬化的传统方法是，通过在刀刃上涂抹绝缘黏土来影响刀浸入水中时向周围水体传递热量。刀身的不同区域会被涂上不同厚度的黏土，刀刃附近涂的黏土层较薄，其他部分涂的黏土层较厚。
热处理过程涉及的多物理场
钢构件的热处理仿真需要确定模型中应涉及的相关物理现象。
从根本上说，热处理过程由与外部热交换产生的热量传递驱动。组件（此处为武士刀）内部温度的变化会引起冶金相变（奥氏体分解为铁素体、珠光体等）。在相变过程中，会产生潜热，从而影响温度。与热膨胀和相间密度差异相关的体积变化会导致组件变形，进而产生机械应力和塑性应变。而众所周知，在存在机械应力的情况下发生的相变会导致材料产生非弹性应变，即所谓的相变诱导塑性（TRIP）。淬火过程本质上是多物理场相互作用的过程，并且各个冶金相具有不同的材料属性，因此会产生平均的、与相组成相关的复合材料行为。
对于本文所建立的武士刀热处理模型，我们进行了以下简化：
- 忽略了相变过程中的潜热
- 忽略了相变诱导塑性应变
武士刀热处理过程中涉及的多物理场如下图所示。
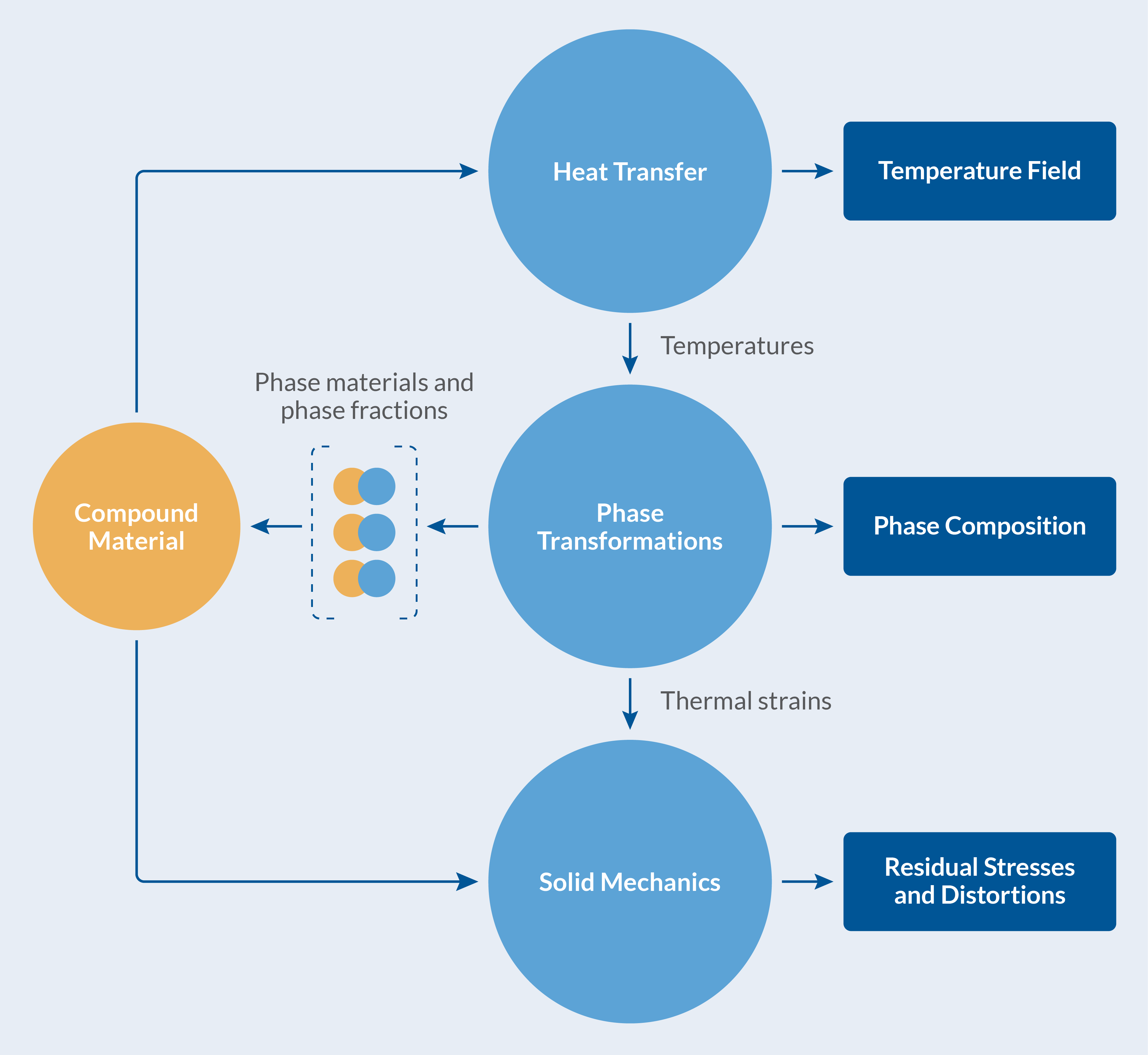
武士刀热处理过程中涉及的多物理场。
武士刀的材料
传统的武士刀制作是在刀刃的不同部分使用不同类型的钢材。通常，刀刃与刀身内芯材料不同，最显著的区别是碳含量不同。碳含量以及其他合金元素的含量对钢材的热性能和机械性能以及相变特性都有很大影响。在此，我们将其简化为单一钢材，其合金含量如下表所示：
| 元素 | 重量百分比（wt%） |
|---|---|
| C | 0.63 |
| Mn | 0.9 |
| P | 0.04 |
实际上，钢材中还含有其他合金元素，但为了简单起见，除碳（C）之外，我们只考虑锰（Mn）和磷（P）。
武士刀的几何结构
武士刀的几何结构，刀身长度为 50 cm（左），刀身横截面高度为 2.8 cm（右）。
相变仿真
不同相组成的钢材性能不同，因此需要对各种可能的相变进行表征。在室温下，钢的基本组成为 50% 铁素体和 50% 珠光体。首先加热武士刀，直到其基本组成完全转变为奥氏体。然后在水中淬火，以获得最终的相组成。这种相组成在空间上会有所变化，通常是铁素体、珠光体、贝氏体、马氏体以及可能的残留奥氏体的某种组合，见下图。材料相的空间变化受每个材料点在冷却过程中所经历的温度的影响。
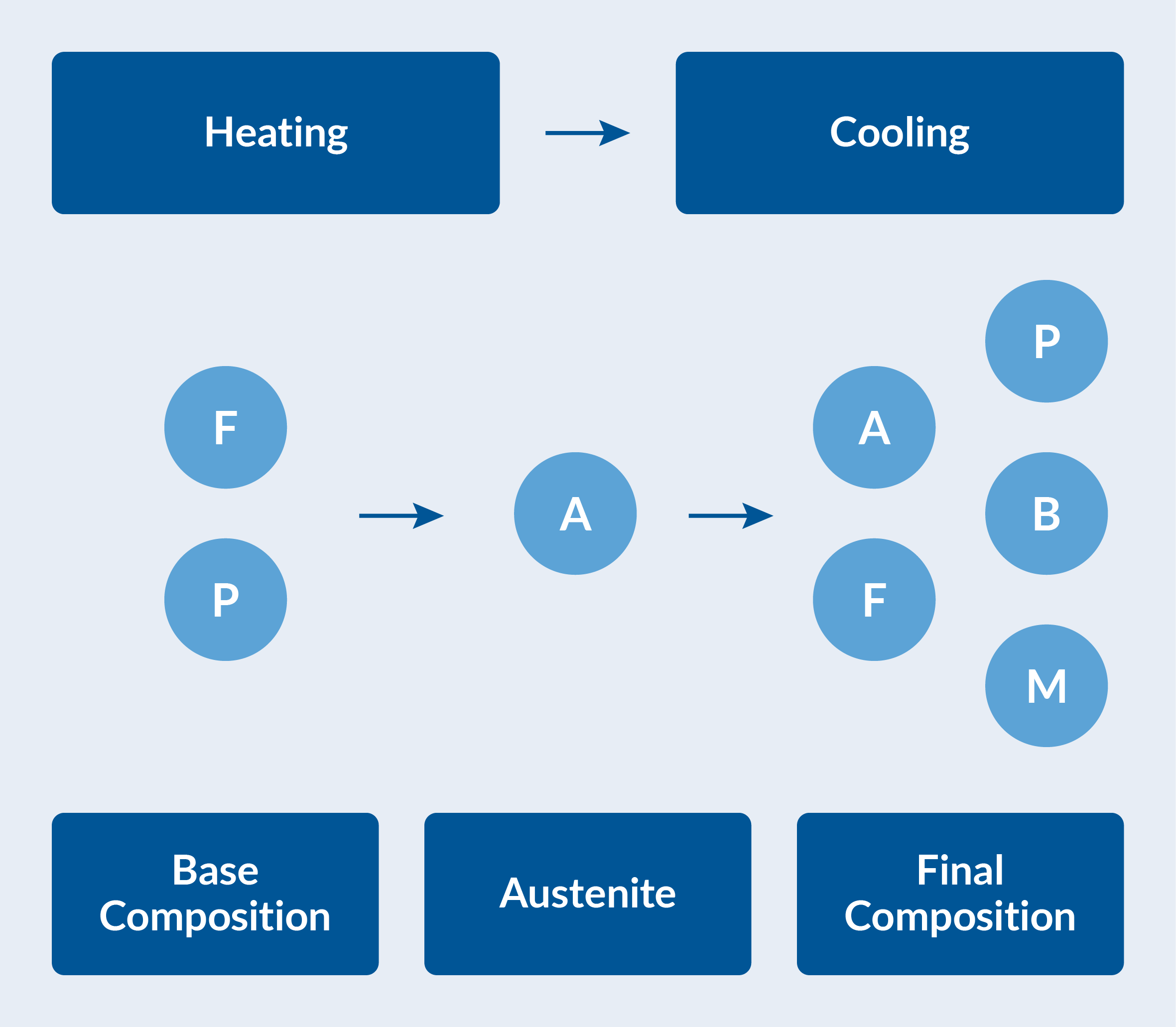
加热和冷却过程中的相组成。铁素体（F）和珠光体（P）的基本组成在加热时转化为奥氏体（A）。奥氏体在冷却过程中分解为铁素体、珠光体、贝氏体 (B) 和马氏体 (M)。
加热
加热模拟不仅是为了模拟铁素体-珠光体钢的奥氏体化，也是为了模拟加热时产生的热应变。请注意，我们本来可以在冷却开始时施加初始应变，以包括热应变，从而忽略加热，但我们选择在冷却模拟前进行加热模拟。不过，由于我们并不关心奥氏体的形成本身，因此使用 Leblond-Devaux 相变模型来模拟铁素体-珠光体基本组成中奥氏体的形成。相变模型使用了 附加源相 子节点，因此铁素体和珠光体在奥氏体的形成过程中都是源相。奥氏体 (A)、珠光体 (P) 和铁素体 (F) 的相分数速率分别由以下公式给出：
其中，奥氏体的平衡相分数为 1（完全奥氏体化），时间常数设为 60 s:
此外，我们只允许在加热过程中进行这种相变，具体方法是使用 变换条件 子节点， 在该节点中输入以下条件 c:audc.Tt>0。
冷却
当完全奥氏体化的武士刀在水中淬火时，奥氏体会分解成铁素体、珠光体、贝氏体和马氏体的组合。整个刀身不同位置的冷却速度，会形成不同的相含量。这表明，与加热模拟相比，冷却模拟时需要对相变进行更详细的描述。因此，使用 Johnson–Mehl–Avrami–Kolmogorov(JMAK) 相变模型模拟奥氏体分解为铁素体、波来石和贝氏体的过程。该模型适用于扩散相变模拟。它有三个参数：
- 平衡相分数, \xi_\mathrm{eq}
- 时间常数, \tau
- Avrami 指数, n
平衡相分数表示目标相的平衡相分数，可视为长期渐近线。例如，对 Fe-C 图中的奥氏体和铁素体两相区域应用杠杆原理，就可以计算 A_{e1} 和 A_{e3} 温度之间的铁素体平衡相分数。要确定其余参数，可以利用时间-温度-转变 (TTT) 图。TTT 图通常显示每种冶金相开始形成的时间和每种转变结束的时间。TTT 图假定在等温条件下进行，也就是说如果要通过实验获得 TTT 图，首先应将试样快速冷却到“目标温度” T_\mathrm{0}，然后保持在该温度。在一定温度范围内，通常是从奥氏体化温度到马氏体形成温度范围内重复这一过程。
下列示意图中，下半部分显示了一个 TTT 图，其中两条曲线分别表示形成 1% 和 99% 的目标相所需的时间。这些分数都是相对相分数，表示在每个温度水平下，目标相与该温度下可达到的最大值的比例。相对相分数由 X =\xi^\mathrm{d}/\xi^\mathrm{d}_\mathrm{eq} 给出，其中平衡相分数一般与温度有关。请注意，如果已经通过实验确定了这两条 TTT 曲线，就可以在每个温度下精确拟合 JMAK 相变模型。然后，中间相对相分数将由 JMAK 模型的公式决定。示意图的上半部分显示了在 T=T_0 下，由特定相变模型控制的目标相的演变过程。
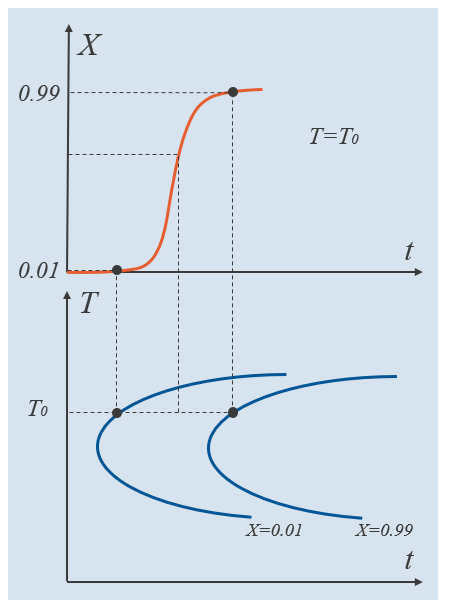
相对相分数为 0.01 和 0.99 时的 TTT 曲线示例。图中标出了中间相对相分数。
在 COMSOL Multiphysics® 中，JMAK 相变模型以速率形式表示，因此适用于非等温条件。不过，在 TTT 意义上，我们可以对 JMAK 模型进行符号积分。目标相随时间的演变过程变为：
经过一些处理后，可以将这个等式重新写为：
如果使用上图中的开始和结束时间以及相分数，假设平衡相分数已知，就可以确定 Avrami 指数 n 和时间常数 \tau:
这正是 相变 节点中 JMAK 相变模型的 TTT 图数据 表述方式。
在当前的武士刀淬火模型中，我们使用了三组虚构但合理的开始和结束 TTT 曲线，分别将奥氏体分解为铁素体、珠光体和贝氏体。铁素体数据的一部分如下表所示：
| T \, (^{\circ}C) | t_1 \, (s) | t_{99} \, (s) |
|---|---|---|
| 575 | 2.2 | 43 |
| 580 | 0.22 | 2.1 |
| 585 | 0.075 | 1.42 |
| 590 | 0.076 | 1.47 |
| 595 | 0.078 | 1.47 |
| 600 | 0.079 | 1.49 |
| 605 | 0.081 | 1.54 |
| 610 | 0.084 | 1.58 |
| 615 | 0.086 | 1.63 |
| 620 | 0.090 | 1.70 |
| \vdots | \vdots | \vdots |
| \vdots | \vdots | \vdots |
| 730 | 5.8 | 110 |
| 735 | 13 | 254 |
| 740 | 41 | 820 |
| 745 | 322 | 6246 |
为了完成相变模型的定义，还需要确定:
- 铁素体、珠光体和贝氏体在各自相变过程中与温度相关的平衡相分数。
- 相变的温度上限和下限。例如，A_\mathrm{e3} 定义了铁素体转变的起始温度，而 M_\mathrm{s} 则是马氏体的起始温度。
平衡相分数和不同的转变温度使用 奥氏体分解 接口下的 钢成分 节点，根据化学成分计算。
我们只允许在冷却过程中发生这些相变，与加热过程一样，使用 相变条件 子节点 控制，在该节点输入以下条件 c:audc.Tt<=0。
当结合使用铁素体、珠光体和贝氏体相变的 TTT 曲线时，就可以使用 奥氏体分解 接口计算出 TTT 图。下图显示了计算出的 TTT 图。为了模拟这种情况，我们在零维中使用 奥氏体分解 接口，并通过选择相节点中的 计算转变时间 来获得达到特定相分数的时间。
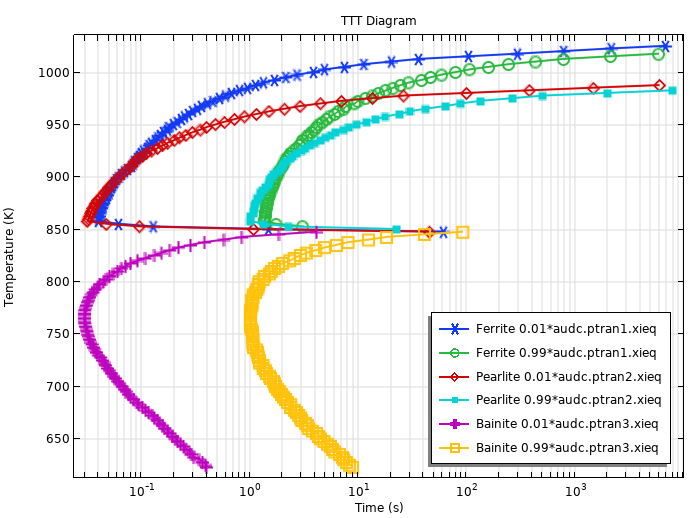
使用虚构的 TTT 数据计算出的 TTT 图。
马氏体相变由 Koistinen–Marburger 相变模型描述。定义该模型需要两个参数：
- Koistinen–Marburger 系数，\beta
- 马氏体开始温度，M_\mathrm{s}
与等温条件下考虑的扩散铁素体、珠光体和贝氏体转变不同，马氏体转变本质上取决于温度速率。根据 Koistinen–Marburger 模型，马氏体的形成速率通过 \beta 系数与冷却速率成正比。
在定义了所有相变之后，我们还可以计算连续冷却转变（CCT）图。下图所示为 CCT 图，其中奥氏体化温度为 900 °C，冷却速度范围为 0.1 K/s 至 1000 K/s。图中的 1% 线表示已形成的铁素体、珠光体、贝氏体和马氏体相。奥氏体也显示了 1% 线，表示奥氏体分解完成，即几乎所有奥氏体都分解成了其他相。
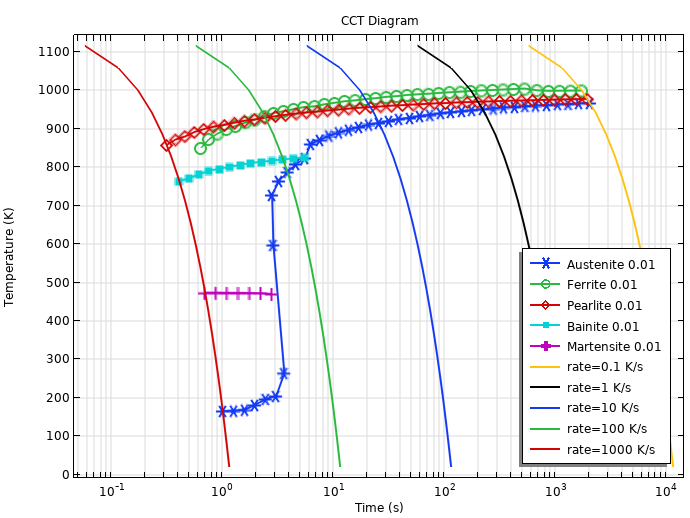
根据 TTT 数据计算的 CCT 图。
材料的机械和热性能
要建立武士刀这样的钢铁组件的淬火过程的详细模型，需要了解其机械和热性能。这些性能在不同相（如奥氏体和铁素体）之间存在差异，而且还取决于温度。对于弹塑性特性，一般还取决于应变和可能的应变率。通过实验获得一整套材料特性既耗时又昂贵，因此往往难以实现。在实践中，会使用其他来源，包括文献中的实验数据和计算的材料特性。本模拟的目的是演示武士刀的淬火过程，因此我们对模型进行了如下简化：
- 弹性特性在各相之间保持一致，但其余特性在各相之间有所不同。
- 导热系数和热容量与温度有关。
- 初始屈服应力与温度有关。
- 各相的硬化行为是线性的、各向同性的，并且与温度有关。
- 热膨胀系数不变，但体积参考温度不同。
各相的材料特性与演变的相组成（相分数）可一起用于计算有效材料属性。这项工作是在金属加工模块中自动完成的，计算出的有效材料属性被收集在 复合材料 中，与其他物理场接口共享，见下图。
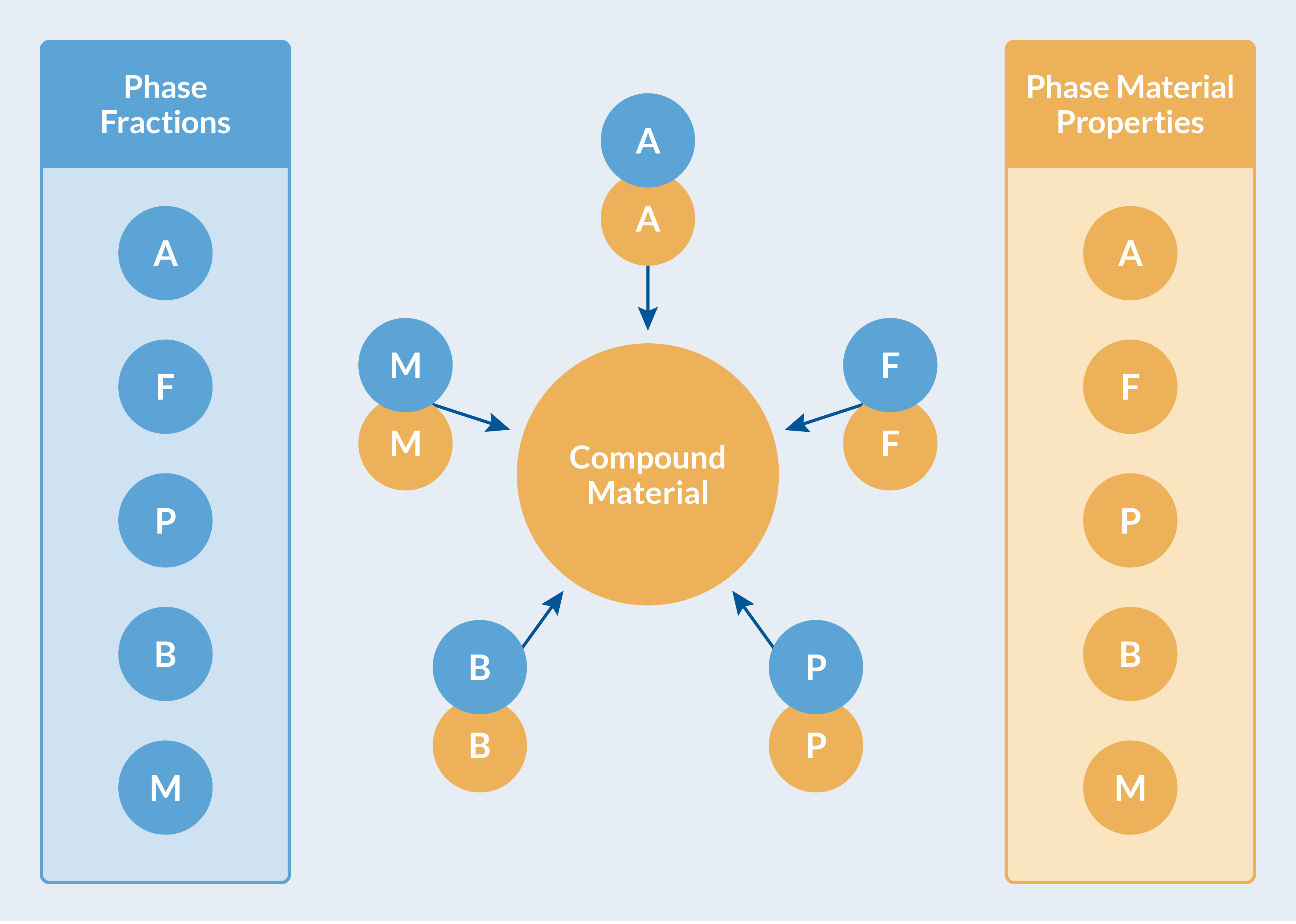
计算出的有效材料属性被收录在 复合材料 中 。
传热仿真
使用 固体传热 接口来模拟武士刀内的热传递以及与周围环境的热交换。为简化问题，我们忽略了辐射传热，仅通过对流传热来模拟刀刃到周围环境的热传递。在刀片表面指定了一个热通量，并使用与温度相关的热传导系数表征。
加热
加热武士刀是为了使铁素体-珠光体基本组分奥氏体化。为了模拟这一过程，我们使用了一个简化的对流模型，采用恒定的传热系数 300W/m^2K 。在加热的第一分钟内，环境温度从室温跃升至 850°C，然后在整个加热过程中保持恒定。选择总时间是为了使材料完全转变为奥氏体，并且加热时武士刀内的热梯度要足够低，以防止热致塑性应变。
冷却
为了模拟不同厚度的隔热黏土的效果，刀片边缘附近区域的传热系数与刀片上部的有所不同。
下图显示了表示薄层和厚层黏土随温度变化的传热系数。
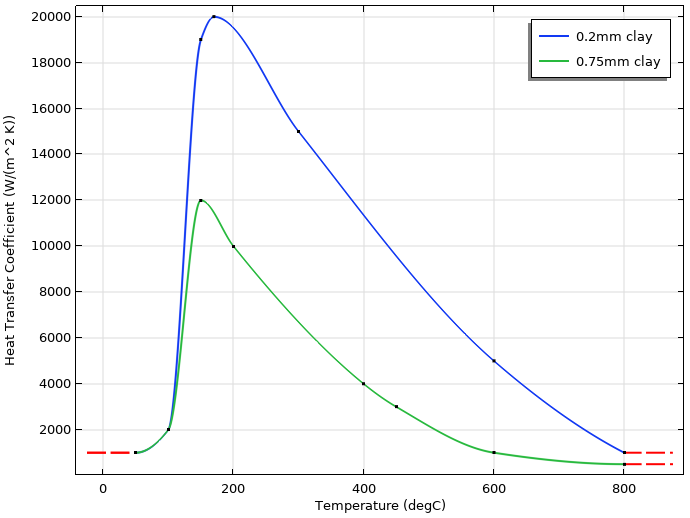
薄层（0.2 mm）和厚层（0.75 mm）黏土随温度变化的传热系数。薄层用于刀片边缘，厚层用于刀片其余部位。
应力和应变仿真
使用 固体力学 接口计算武士刀在热瞬态过程中的应力、应变和变形。我们在前面已经指出，热膨胀和各相之间的密度差异会导致组件变形以及机械应力和塑性应变。因此用 奥氏体分解 接口模拟这些效应，并通过 相变应变 多物理场耦合转移到 固体力学 接口。我们预计武士刀会有明显的弯曲。细长结构的弯曲不一定会产生较大的材料应变，但是会涉及有限旋转，因此分析是几何非线性的。预计弯曲也会产生塑性应变，因此使用 线弹性材料 的 塑性 子节点考虑这一点。
结果
武士刀最显著的特征之一就是刀刃弯曲。有趣的是，这种弧度是在淬火过程中产生的，而不是在热处理之前将刀刃弯曲所致。由于刀刃靠近边缘的部分较薄，隔热黏土也涂得更薄，因此温度迅速下降，刀刃最初会随着奥氏体冷却和收缩而向下弯曲。当温度降至马氏体开始温度以下时，奥氏体开始转变为马氏体。转变为马氏体的过程伴随着体积膨胀，从而在刀片边缘产生压应力。随着冷却向刀脊部位推进，冷却速度降低，其他冶金相也随之形成。刀刃从最初的向下弯曲过渡到最终的传统弧形。下图显示了冶金相的最终组成。值得注意的是，刀刃是马氏体，因此硬度较高，但刀脊主要是珠光体，因此韧性更好。
冷却时的马氏体相分数（上）、轴向应力（中）和温度（下）。
淬火后的最终组成。刃口具有理想的硬马氏体结构，刃脊大部分为珠光体。
学以致用
在这篇博客中，我们展示了如何使用 COMSOL Multiphysics® 模拟武士刀的淬火过程。通过仿真，我们解释了武士刀的弯曲形状是如何形成的，以及使用黏土进行局部淬火的简化传统工艺如何制作出刀刃硬而刀芯软的刀片。当然，对武士刀进行建模只是出于我们的好奇心，但它表明 COMSOL Multiphysics® 可用于模拟一般的钢淬火，不仅可以计算冶金相的组成，还可以预测变形和残余应力。
动手尝试
想尝试自己建立武士刀的局部淬火模型吗？COMSOL 案例库中提供了相应的模型文件，欢迎下载。
评论 (0)