
正如之前在 “非线性问题的载荷递增“博客中所讨论的,当求解一个问题时,我们可以从一个已知解的无载荷问题开始,然后使用延拓法逐渐递增载荷来进行求解。这个算法同样适用于理解接近失效的载荷时的情况。然而载荷递增并非适用于所有情况,在某些情况下可能无法发挥效用。本篇博客中,我们将介绍如何通过非线性递增改进问题的收敛。
非线性递增示例
再次考虑下图中含非线性刚度的弹簧系统,对其施加应力。
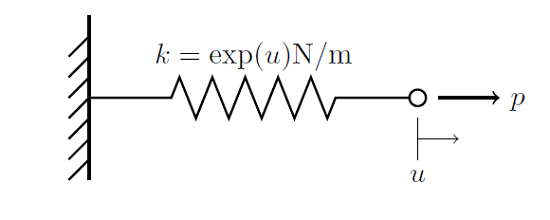
我们发现可以使用阻尼 Newton 法求解该问题,或是使用延拓法并递增载荷,从而为 Newton 法提供一个好的初始条件。现在我们来检验如何递增非线性。首先,让我们再来看一看描述单一节点上受力平衡的方程:
可将以上等式写成通式:f(u)=p-k(u)u ,其中 k(u) 是非线性弹簧刚度。现在我们可以使用以下刚度来求解不同的问题:
也就是说,我们将弹簧的刚度方程分为两部分:一个线性项 k(u_0),以及一个非线性项 \left[ k(u) – k(u_0) \right],接着引入一个附加参数 \beta,插入在线性项和非线性项之间。然后对一系列带有参数 \beta 的问题使用与之前相同的 Newton 法,并使参数 \beta 从 0 递增到 1 。也就是说,使用延拓法从一个(容易求解的)线性问题递增到一个(更难的)非线性问题。
接下来使用这种该法求解上述例题。初始弹簧刚度 k(u)=\exp(u)被改写成:
我们从求解 \beta=0 的情况开始,得到一个线性弹簧刚度 k(u)=\exp(u_0),所以现在需要做的就是找到一个线性化起点 u_0。在这个案例中,如果选择 u_0=0,那么 f(u,\beta=0)=2-\exp(0)u = 2-u。回想之前关于求解线性稳态有限元模型的讨论,我们学到总能使用一次 Newton 迭代来求解线性问题。现在递增参数 \beta,结果如下:
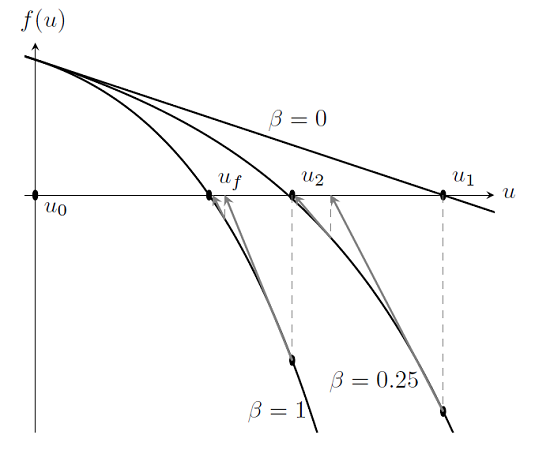
可以明显看到,只有一小部分从 \beta=0 开始的解需要对 \beta=0.25 求解。所以我们可以重复 \beta=1 的步骤并从完全线性情形递增到完全非线性情形。
这一方法很有吸引力,因为我们总能找出线性问题的解,所以总能求解 \beta=0。您只需考虑该对哪些点 u_0 进行初始线性化以及应该使用哪种非线性递增。
我们也可使用非线性递增的概念来解决非线性项不连续可导的情形。让我们回忆一下求解非线性稳态有限元问题 博客中的案例:具有分段常数弹簧刚度的系统,u\le1.8 时 k=0.5,1.8<u<2.2时k=1 ,以及 u\ge2.2时 k=1.5,将构成受力平衡方程:
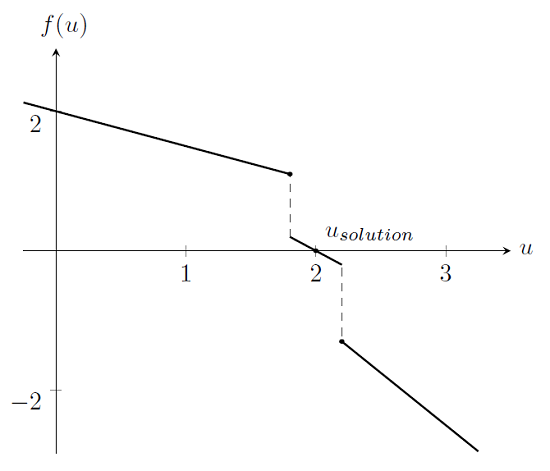
正如之前看到的,这个问题无法用 Newton 法求解,除非您碰巧在解的(非常小)收敛半径内开始求解。但现在考虑将原始的弹簧刚度替换为可以递增的平滑刚度:
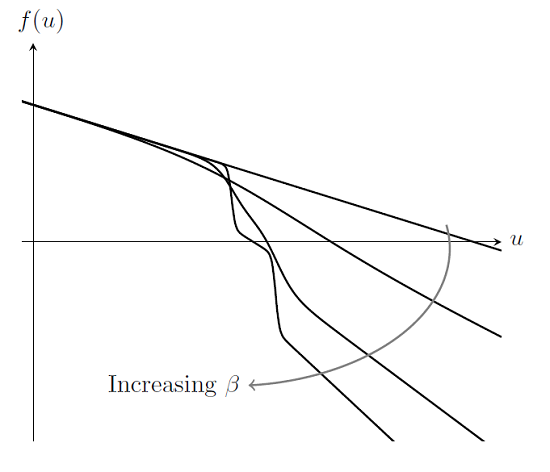
显然该问题可以求解,而且我们可以使用这个方法得到原始问题的大致解,它仅要求我们得出一个大致的平滑方程和非线性递增路径。
当您遇到具有上述阶梯行为的问题时,就可以尝试使用双折线非线性求解器代替 Newton 法。双折线求解器是一个置信域求解器,适用于求解 Newton 法可能会在不同区域内震荡的问题。结构接触问题就是这类问题的良好物理示例,即当两个物理进行物理接触时,会产生载荷的突然转移。
改善非线性问题收敛性的结束语
我们已经介绍了两种改善非线性问题收敛性的方法:载荷递增和非线性递增。在实际操作中,您可以选择其中的一种做法,以及对材料属性及载荷进行恰当设置,从而能够结合这两种做法。很难说哪种方法的表现更优异,对于每个模型,您可能需要进行一些不同的尝试,包括载荷递增路线、非线性递增以及线性化初始条件的选择等。同样,当您预期解可能会在不同情形下产生震荡时,双折线求解器会比 Newton 法更有效。随着经验的增加,您将能形成一种工程直觉,从而能够找出所求解问题的最佳求解方式。
博客中介绍的方法,主要适用于求解难以找到良好初始条件的非线性稳态有限元问题,或者包含强非线性以及不连续性材料属性的问题。实际操作中,您将能通过这些方法解决很多问题。此外,您还应注意到,求解非线性问题时需要不同的网格剖分方法。这将是我们接下来会阐述的主题,请继续关注。



评论 (0)