从测量中获取结构力学的材料数据（第二部分）

在本系列的第一篇博客中，我们讨论了将测量材料数据转化为本构模型时的一些注意事项；并详细介绍了超弹性材料。今天，我们将讨论如何使用非线性弹性和弹塑性材料，并将介绍一种您可以直接在 COMSOL Multiphysics 中使用您的测量数据的方法。

非线性弹性材料

一些材料会在较小的应变下表现出明显的非线性，例如，铸铁和部分陶瓷；但当移除这个较小的应变时，材料又将按照同样的应力-应变路径返回初始态，作出弹性响应。这就是非线性弹性模型。

我们在之前一篇博客中讨论了超弹性材料，那为什么不能通过其中的一个模型来拟合材料（比如球墨铸铁）的应力-应变测量曲线呢？答案是超弹性材料模型适用于较大的应变。弹性体的长度可能达到原始长度的数倍，而金属和许多脆性材料的弹性范围通常小于 1%。

例如非常受欢迎的 Mooney-Rivlin 模型，它在小应变下的表现就基本为线性，因此不适用于本博客所讨论的情况。在 Ogden 模型中，将应力作为拉伸力的总和计算。但对于小应变，拉伸范围大约为从 0.999 到 1.001。为了预测明显的非线性，幂律指数应非常高。我们无法对该方程执行数据的稳态拟合。对于脆性材料中存在的小应变，可以通过工程应变更自然地表征变形。您可以在博客”为什么需要所有这些应力及应变“中读到有关各种应力和应变测量的介绍。

为了解决这一问题，COMSOL 针对小应变提供了一组非线性弹性模型。这些材料模型位于固体力学和膜接口下，需要耦合非线性结构材料模块或岩土力学模块。我们将分析如何使用这些材料。

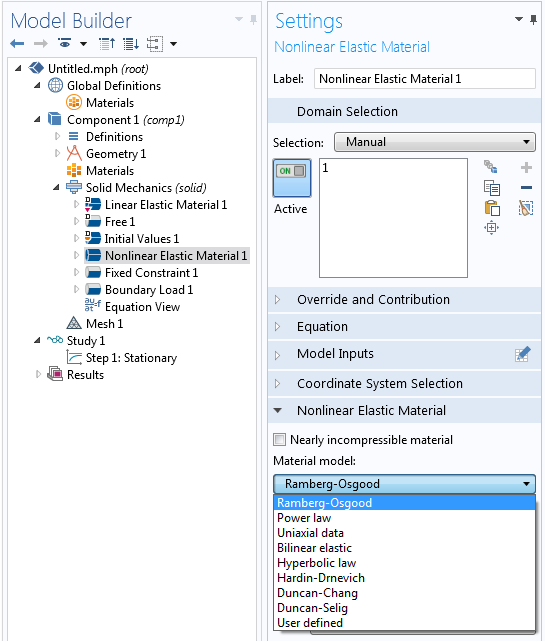
在 COMSOL Multiphysics 中选择非线性弹性材料模型。

COMSOL 共提供了 9 个非线性弹性材料模型，部分模型包含由几个参数决定的简单数学公式。其中一个材料模型特别适合用于处理应力-应变实验数据，即单轴数据。显而易见，该模型是基于测量数据进行分析。我们将分析该模型的设定：

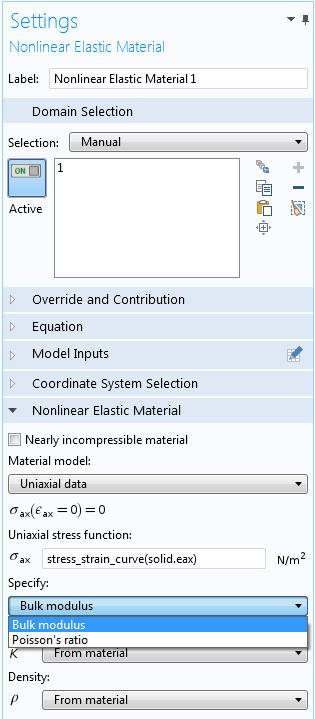
单轴数据非线性弹性模型的设定。

模型的主要输入是单轴应力关于单轴应变的函数。在本示例中，测量数据以内插函数的形式给出，名称为 stress_strain_curve，它也可以是解析表达式。可以通过数据点数量的形式显式输入内插函数，或直接导入数据文件。这里导入的是 Excel® 文件。操作需要 LiveLink™ for Excel® 附加模块、不过也支持从列表文本文件中读取数据。

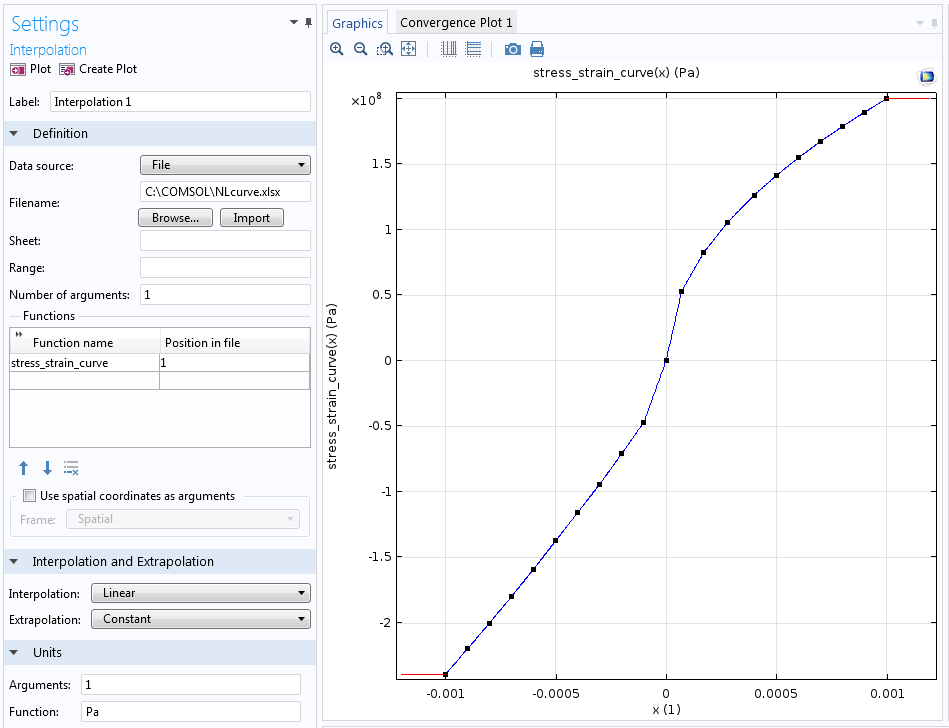
导入的单轴应力-应变曲线。

但单轴曲线提供的信息不足以完整定义多轴本构定律。因此将需要再做一个假设，这也是您需要提供常泊松比或体积模量的原因。对许多材料而言，泊松比为介于 0.2 到 0.3 之间的常数就能给出一个较好的近似。这也是我们完成材料模型所需的全部信息。

如研究上方的应力-应变曲线，您将发现拉伸与压缩下的曲线不同。但在多轴应力状态下，材料中的某个点可能在一个方向经历拉伸，并在另一个方向经历压缩。那应使用材料曲线的哪个分支呢？材料模型为各向同性，因此所有方向的刚度相同，但体积变化才是决定因素。如果局部体积变化为负，那就应使用压缩分支。

理论注解

从理论角度来看，只应在以下情况采用各向同性非线性弹性材料：

• 平均应力（“压力”）或体积模量只是体积应变的函数。
• 剪应力或剪切模量只是剪应变的函数。

如果违反这些条件，您可以设计一个支持能量提取的应力-应变循环，也就是永动机。

所有内置材料模型都能满足上述条件。例如，在双线弹性材料的设定，您需要输入拉伸与压缩的体积模量，而非您之前设想的杨氏模量。

大部分结构分析会将杨氏模量和泊松比作为弹性材料的主要参数。但上述要求规定如果杨氏模量依赖于应变，那么……

• 描述该依赖性的函数只能有一些非常具体的形式。
• 泊松比也必须为应变的函数，因此该函数将非常难以表达。

那如何才能在上方输入一个带有常泊松比的单轴数据？答案是我们定义一个关于体积模量和剪切模量的容许函数。这个函数与杨氏模量无关，即使这是您能直接从图中获取的结果。

即使如此，我还是见过不少成功模型，它们在各向同性和正交各项异性弹性材料模型的杨氏模量中引入了应变依赖关系。从工程实际来讲，这的确行得通。在弹性随应力变化的材料教程模型中，我们介绍了如何定义依赖于应力的杨氏模量。此方法的使用关键在于结构正在承受的主要为比例载荷，即主应变的方向不旋转。

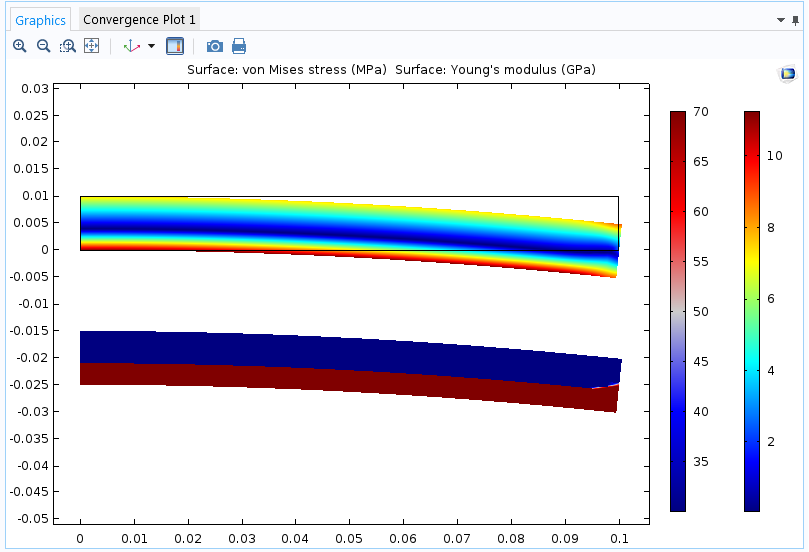
悬臂梁处于拉伸和压缩状态时杨氏模量的不同值。在梁的自由端施加了一个弯矩。上图为 von Mises 应力；下图为杨氏模量的当前值。

当您通过内置模型或自定义表达式模拟非线性弹性时，需要明确区分切线刚度和割线刚度。非线性弹性模型的表达式通常与线性模型类似，但弹性系数会依赖于应力或应变，因此它不再是一个常量！假定剪应力 \tau 与剪应变 \gamma 满足如下关系式

那么，剪切模量 G_S(\gamma) 应为割线剪切模量。用总应变乘以割线模量，得到总应力。另一方面，切线剪切模量 G_T(\gamma) 是应变发生微小变化时经历的刚度，如下图所示。

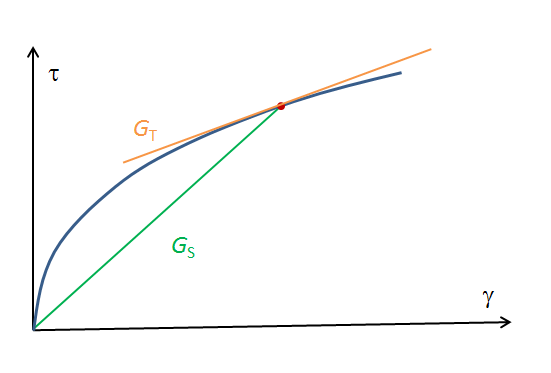
从数学角度来看，两个模量间的关系为：

您的测量数据通常为以下形式

意思是割线刚度实际为：

当使用此表达式将应力-应变曲线转化为割线形式时，特别应考虑零应变下的除零问题。

此外，您还可能碰到某个材料已被拟合到含特定指数 n 的幂律中的情况。这可能意味着

或

COMSOL Multiphysics 的幂律模型中用到了更通用的第一个定义，在半对数绘图中，应变指数 n 与应力-应变曲线的斜率相关。

通过非线性弹性近似塑性

纯拉伸试验无法确定测量得到的特定非线性是否由塑性造成。此时，还应再分析卸载曲线。下方动画取自之前的一篇博客，较好地表示了这一点。

非线性弹性材料简介博客介绍了如何通过非线性弹性模型模拟塑性。

除了使用单轴数据模型，还可以简单通过 Ramberg-Osgood 非线性弹性材料模型来替代完整的弹塑性模型。使用非线性弹性材料的计算成本明显要低，但它的使用限制呢？

• 显然，载荷只能持续上升。
• 如果同时承载了多个外部载荷，例如，压力载荷与热膨胀，它们通常与彼此不成比例，可能使局部应力变为非比例。
• 三维响应通常并不相同，即使单轴应力-应变曲线与非线性弹性模型和全弹塑性模型完全相同。对金属塑性而言，比如 von Mises 流动法则，塑性变形将保持体积不变。在对应的非线性弹性模型中，情况并非如此。

结束语

当选择适合的材料模型时，您必须考虑整个分析的精度。在工程领域，我们通常会碰到各类问题，比如信息不完整，载荷、材料的同质性以及结构实际尺寸不确定等。您还可能会在选择边界条件时引入一些近似。但整个工程项目的质量往往取决于最薄弱的一环，而它也许并非材料模型的精确数学基础。

在之前的博客中，我曾提到过“简单将应力-应变曲线作为输入并不见得是一个好方法。”

那为什么我今天会改变观点呢？答案是我们在处理单轴数据模型时将使用真实的测量。对所有的超弹性模型和大部分的非线性弹性模型而言，必须将测量数据拟合至含多个参数的数学模型中。如果没有人为的监督，我们将很难安全地进行拟合。