在本系列的上一篇博客文章中,我们阐释了在为真实带电粒子束的释放和传播建模过程时,需要考虑的两个必要概念。首先,我们引入了纯数学意义上的概率分布函数,然后探讨了一种特定的分布类型——二维带电粒子束的横向相空间分布。在本篇文章中,让我们结合所学知识,探究如何对这一类分布中的三维粒子束的初始位置和速度进行取样。
回顾椭圆形二维相空间分布
在开始本篇文章前,首先我们来简单地回顾一下在束流物理中的相空间分布系列的上一篇博客文章中,详细介绍过的二维相空间分布。在真实环境中,非层带电粒子束中的粒子占据了相空间的一部分区域,且该区域通常呈椭圆形。二维相空间椭圆的方程式基于束流发射度 ε 和 Twiss 参数,
(1)
其中,x 及 x’ 分别表示粒子的横向位置和倾角。Twis 参数进一步构成了 Courant-Snyder 条件,
(2)
椭圆区域中粒子的实际位置是可以改变的。两种最常见的相空间密度分布是椭圆内的均匀密度分布与最大值位于椭圆中心处的高斯分布,如下图所示。左右两侧的蓝色曲线均为由方程(1) 描述的相空间椭圆,其中 ε 表示 4-rms 横向发射度。值得注意的是,对高斯分布而言,仍然有一些粒子游离于椭圆之外。这是因为高斯分布始终没有下降为零,所以无论绘制的椭圆有多大,总会有一些粒子位于椭圆之外。当使用 4-rms 发射度来定义方程(1)中的椭圆时,则大约有 86% 的粒子位于椭圆之内。
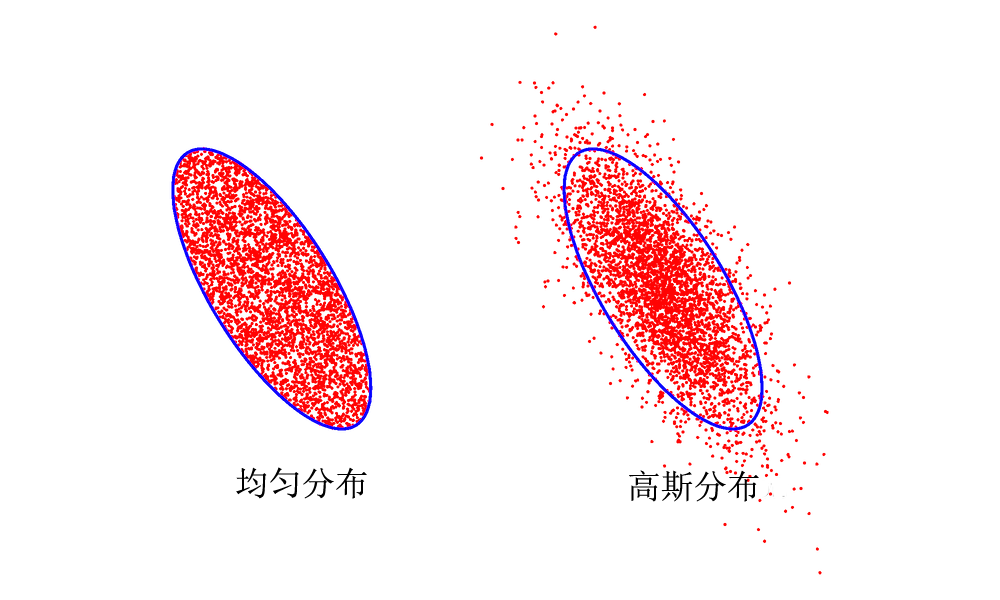
对比均匀分布与高斯分布。
让我们先来考虑一种更简单的情况:在相空间椭圆内的任意一点找到粒子的概率是相同的,而在椭圆外为零。对于这个问题,我们将方程(2)带入方程(1)并求解 x’ 的值
(3)
随后可推出以下概率分布函数
(4)
\begin{array}{cc}
C & -\frac{\alpha x}{\beta} -\frac{\sqrt{\varepsilon \beta -x^2}}{\beta} \textless x' \textless -\frac{\alpha x}{\beta} + \frac{\sqrt{\varepsilon \beta -x^2}}{\beta}\\
0 & \textrm{otherwise}
\end{array}\right.
其中,常数 C 取决于椭圆的大小。粒子概率 g(x) 在给定的 x 坐标下可以表示为
若要将方程(3)取实值的位置也纳入考虑,我们可以将方程写为
\begin{array}{cc}
2C \frac{\sqrt{\varepsilon \beta -x^2}}{\beta} & -\sqrt{\varepsilon \beta} \textless x \textless \sqrt{\varepsilon \beta}\\
0 & \textrm{otherwise}
\end{array}\right.
或将其简化为,
(5)
假设我们要用方程(4)中的概率分布函数来对一群模型粒子进行取样。具体的步骤是:首先根据方程(5)对粒子的初始横向位置进行取样,随后指定适当的倾角,将粒子限制在相空间椭圆内。一种实现方式是从方程(5)开始计算累积分布函数,然后再使用伪随机抽样的方法。另一种可取的途径是利用方程(5)来定义粒子密度,这时我们可以直接在粒子追踪接口的入口 和释放 特征中输入粒子密度表达式。输入完成后,系统便会自动完成归一化。
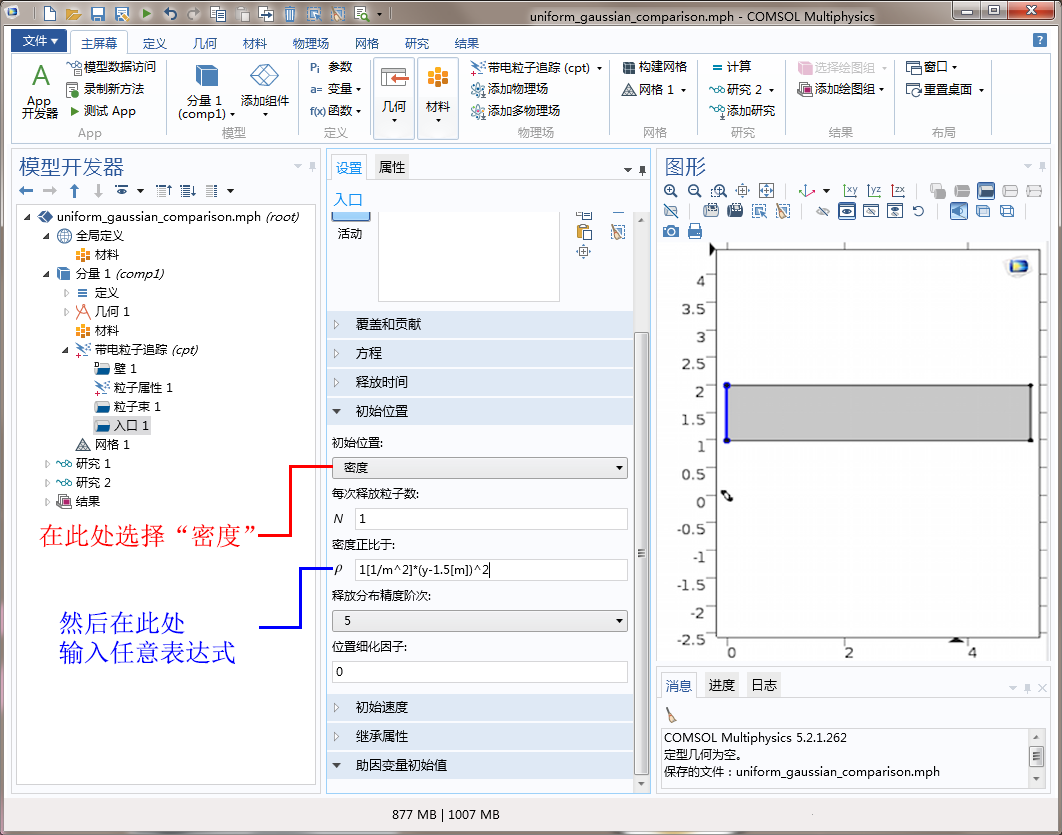
截图显示了如何在“入口”特征中输入粒子密度。
不过,最简便的方法是使用带电粒子追踪 物理场接口中的粒子束 特征。“粒子束”特征可以自动分配相空间中的粒子,同时还能指定粒子束的中心位置、发射度以及 Twiss 参数。
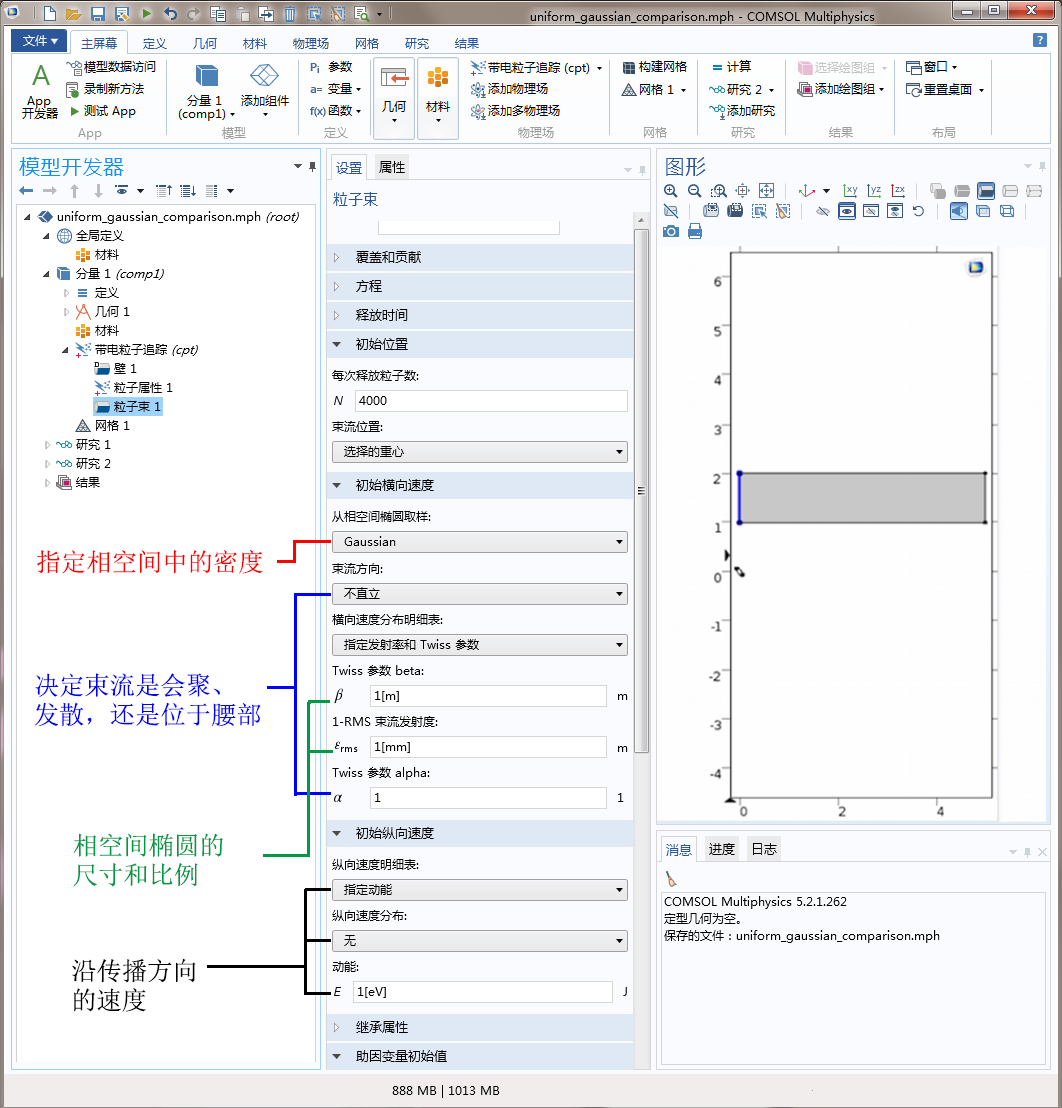
截图显示了如何在“粒子束”特征中输入粒子密度。
模拟三维带电粒子束
到目前为止,我们只对理想化的带状电子束进行了探讨,而忽略了横向位置和速度的面外(y)分量。真正的光束是在三维空间内传播的,并且在两个横向方向上仅延伸了有限的距离。因此,为了绘制完整的束流图像,我们必须引入两个相互正交的横向方向 x 和 y,以及倾角 x' = v_x/ v_z 和 y' = v_y/v_z。

粒子束在三维空间内的传播图像。
相比于二维空间,在三维空间中模拟离子束的释放更加复杂,这是因为在真实的光束中,两个横向方向上的自由度经常会发生耦合。举例来说,假设两个粒子在同一个横向位置上被释放,即 x 坐标和 y 坐标相同。若两个粒子在 x 方向(x’)上的倾角存在大小之分,那么在 x 方向上倾角较大的粒子在 y 方向上的倾角会较小,反之亦然。因此,我们不能只从两个不同的分布中对 x’ 和 y’ 进行取样,因为每个值都会影响另一个值的概率分布。
简而言之,这是因为粒子的横向运动实际上在四维相空间分布中才能进行准确的描述,而不是将两个横向方向当作独立的二维相空间椭圆。由于习惯于在二维或三维空间中观察物体,我们很难呈现出超过三个空间维度的分布情况。
这一点正是“粒子束”特征的最大优势,其设置可专用于对各种内置四维横向空间分布的初始粒子位置和倾角进行取样。常见的四维空间分布包括 KV(Kapchinskij-Vladimirskij)分布、水袋分布、抛物型分布及高斯分布。首先,我们来讨论最简单的分布 KV 分布,然后对这一组中的其他分布类型进行可视化。
在数学上,KV 分布认为束粒子均匀地分布在相空间内的一个无限薄的四维超椭圆体上,其表达式为
+\left(\frac{r_x x' -r'_x x}{\varepsilon_x} \right)^2
+\left(\frac{y}{r_y} \right)^2
+\left(\frac{r_y y' -r'_y y}{\varepsilon_y} \right)^2 = 1
其中,rx 和 ry 为波束在 x 和 y 方向上的最大值,εx 和 εy 为与两个横向有关的发射度,r’x 和 r’y 为束包络边缘的倾角。
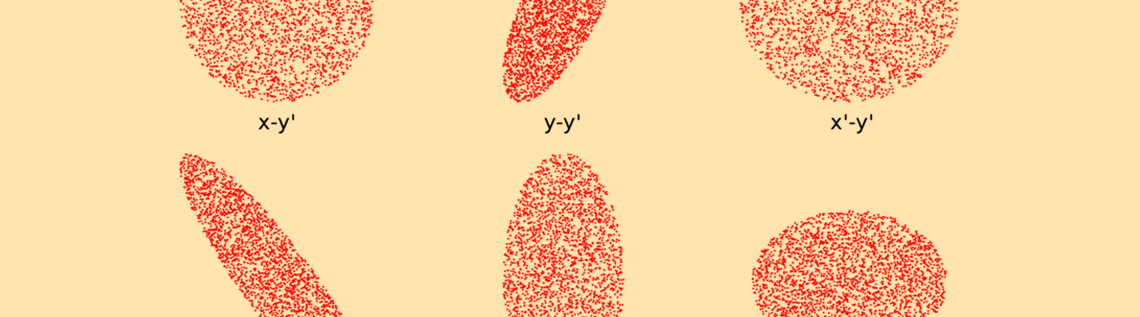
由于四维概率分布函数的可视化比低纬度函数更复杂,通常我们将其投影到较低维度就可以直接实现分布的可视化。KV 分布的一个有趣特性就是,其在任何二维平面内的投影都是一个是均匀密度的椭圆。其在六个平面的投影如下图所示。四维超椭圆体在 x-x’ 及 y-y’ 平面内的投影是倾斜的,因为非零值已指定为每个横向的 Twiss 参数。

六个二维平面内的 KV 分布投影。
对比上方和下方的两组图。
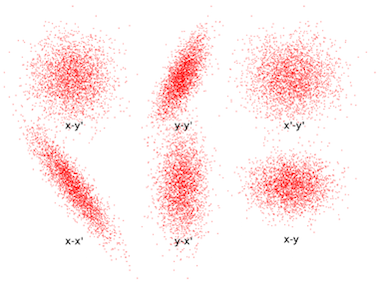
六个二维平面内的水袋分布、抛物线分布及高斯分布的投影。
从上图中我们可以看到,任意情况下二维平面内的投影都是一个椭圆形分布,但只有 KV 分布中的椭圆被均匀填充。
带电粒子束建模总结
有关带电粒子束建模的系列博客到这里就全部结束了,然而我们到目前为止讨论的,仅是束流物理这一复杂技术领域的一些皮毛。当我们讨论三维横向相空间分布时,未涉及到纵向发射度或与此相关的聚束现象。我们也并未区分讨论在束流传播过程中,可能导致其发射度增加、减少或保持不变的现象。
本系列博客文章旨在介绍如何从概率分布函数中进行随机或伪随机取样,以及这种方法对于捕捉真实的高能离子或电子束所起的重要作用。如您想更加深入地了解束流物理学,参考文献 1~3 有将对您大有脾益。如需获取更多关于上文中讨论的四维横向相空间分布的技术细节(包括从这些分布获取伪随机数量取样的算法),您可以参阅参考文献 4~7. 如需深入了解如何在 COMSOL Multiphysics® 软件中应用这些概念,您可以浏览以下资源或联系我们获取相关指导。
查看有关粒子追踪仿真的其他资源
- 查看束流物理中的相空间分布系列的其他博客文章
- 浏览粒子追踪分类中的其他博客文章
参考文献
- Humphries, Stanley. Principles of charged particle acceleration. Courier Corporation, 2013.
- Humphries, Stanley. Charged particle beams. Courier Corporation, 2013.
- Davidson, Ronald C., and Hong Qin. Physics of intense charged particle beams in high energy accelerators. Imperial college press, 2001.
- Lund, Steven M., Takashi Kikuchi, and Ronald C. Davidson. “Generation of initial Vlasov distributions for simulation of charged particle beams with high space-charge intensity.” Physical Review Special Topics — Accelerators and Beams, vol. 12, N/A, November 19, 2009, pp. 114801 12, no. UCRL-JRNL-229998 (2007).
- Lund, Steven M., Takashi Kikuchi, and Ronald C. Davidson. “Generation of initial kinetic distributions for simulation of long-pulse charged particle beams with high space-charge intensity.” Physical Review Special Topics — Accelerators and Beams, 12, no. 11 (2009): 114801.
- Batygin, Y. K. “Particle distribution generator in 4D phase space.” Computational Accelerator Physics, vol. 297, no. 1, pp. 419-426. AIP Publishing, 1993.
- Batygin, Y. K. “Particle-in-cell code BEAMPATH for beam dynamics simulations in linear accelerators and beamlines.” Nuclear Instruments and Methods in Physics Research. Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 539, no. 3 (2005): 455-489.


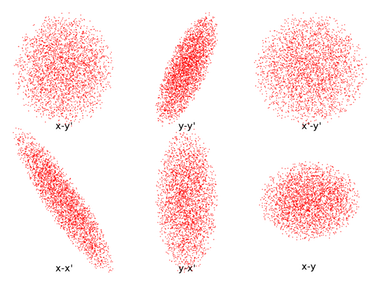
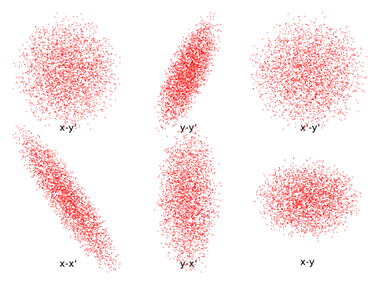

评论 (2)
zang retain
2020-04-23can you send me some tutorial of charged ion motion in electromagnetic filed please ?
王 刚
2020-05-14 COMSOL 员工There some demo examples in Applications Library shipped with COMSOL Multiphysics installation. You can also find these examples in Applications Gallery, e.g., http://cn.comsol.com/models/particle-tracing-module?q=%E7%94%B5.