在上一篇博客文章中,我们讨论了为向后微分法(Backward Differentiation Formulas,BDF)时间步进方法选择时间步和离散阶次的内在机理。这些机理旨在根据指定的容差获得精确解,并保持效率和鲁棒性的平衡。 当碰到较小自动时间步时,我们应采取哪些策略来提高仿真效率?在本篇博文中,我们列举了一些示例,并讨论了如何通过调整求解器设置来应对较小的时间步。
在求解器日志中追踪时间步和离散阶次
当使用 BDF 时间步进方法检查与时间有关的仿真求解器日志时,根据上一篇博客文章中描述的机理,BDF方法的阶次和时间步会发生变化。我们可能会出现以下三种情况之一:
情况 1:变化的时间步和离散阶次
从求解器日志中,我们发现 NLfail=0 和 Tfail=0(瞬态和代数求解器未记录任何失败),但是时间步长和离散阶次都在变化。
对于运行良好的模型,这是一个典型的场景并符合预期。当局部截断误差较小时,时间步长会增加。离散阶次的增加表示具有单调衰减的高阶时间导数的解很平滑。非线性的影响由代数求解器处理,并通过一些额外的代数求解器迭代或某些额外的雅可比(Jacobian)更新反映,但这不会以任何其他方式影响时间步进。
通常,我们不需要每次都调整求解器设置。但是,在我们的实际模拟中,总是存在一些风险:例如,容差太大以及解中的某些效应或细节会丢失;即使所有时间步都满足误差估计,仍无法求解。因此,减小容差并重新仿真是解决这个问题的一个好方法。这会使时间步变得更小并得到精度更高的解,代价是需要更多的 CPU 计算时间。另外,我们还需要注意的是,代数终止的准则与时间求解器的容差直接相关。因此,太大的容差不仅会影响时间离散误差,还会影响终止代数迭代的误差。
因此,在某些情况下,降低容差可以得到具有较好细节的解和更平滑的误差估计,但也会产生更大的时间步。这有点违背常理,因为在这些情况下,降低容差会使时间步进更有效(更快)。
示例:一维黏滞伯格斯方程(Burgers’ Equation)
考虑伯格斯方程
将平滑的阶跃函数作为初始值,扩散系数 c=0.001,对流系数 \alpha=1 和非线性对流系数 \beta=1。
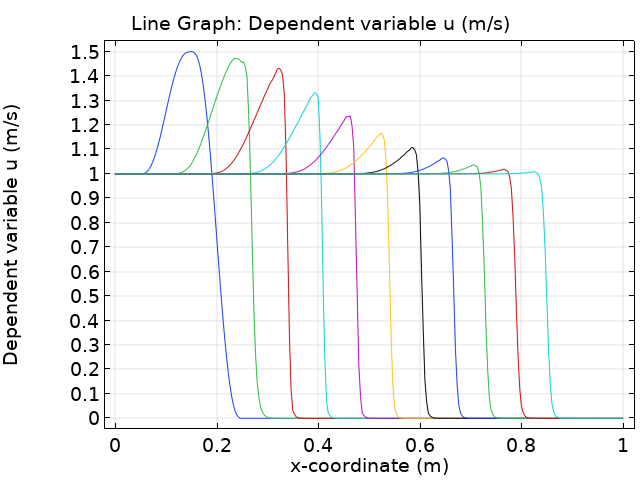
默认的求解器设置在齐次狄利克雷边界条件下,使用二次拉格朗日单元离散在区间 (0,T] \times (0,1) 内求解。由于问题是非线性的,因此形成了一个黏滞冲击的解分布。为了确定合理的网格尺寸和容差,我们首先进行了网格收敛分析。
使用最大单元大小 h_{\rm max} = 1e-6 (对应自由度为 2e6),相对容差 R=1e-5 以及 855 个时间步,对于 T=0.15,得到一个参考解 u_{\rm ref} 。确定最大点误差 e_{P1} := {\rm max}_{t \in (0,T]} |u(t,0.2)-u_{rm ref}(t,0.2)|,e_{P2} := {\rm max}_{t \in (0,T]} |u(t,0.35)-u_{\rm ref}(t,0.35)| ,以及积分误差 e_I := {\rm max}_{t \in (0,T]}\int_0^1 |u(t,x)-u_{\rm ref}(t,x)|dx。如果网格太粗糙或相对容差太大,则解中会出现可见的尖峰(参见下表中的红色数值;尖峰仅反映在 e_{P2} 列中)。
| R=0.01 | R=0.001 | R=0.0001 | R=0.00001 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| h_{\rm max} | # | e_{P1} | e_{P2} | e_I | # | e_{P1} | e_{P2} | e_I | # | e_{P1} | e_{P2} | e_I | # | e_{P1} | e_{P2} | e_I |
| 1e-2 | 106 | 1.5e-2 | 4.9e-1 | 8.1e-3 | 195 | 5.5e-3 | 1.6e-1 | 1.8e-3 | 272 | 9.3e-4 | 1.6e-1 | 1.7e-3 | 380 | 1.6e-3 | 1.6e-1 | 1.7e-3 |
| 1e-3 | 109 | 2.7e-2 | 4.2e-1 | 8.0e-3 | 246 | 6.0e-3 | 1.6e-1 | 1.8e-3 | 508 | 1.7e-3 | 2.1e-3 | 8.3e-5 | 904 | 9.0e-7 | 1.8e-4 | 3.7e-6 |
| 1e-4 | 109 | 2.7e-2 | 4.2e-1 | 8.0e-3 | 246 | 6.0e-3 | 1.6e-1 | 1.8e-3 | 461 | 1.7e-3 | 1.2e-3 | 8.3e-5 | 833 | 1.2e-8 | 3.8e-7 | 1.4e-6 |
| 1e-5 | 109 | 2.7e-2 | 4.2e-1 | 8.0e-3 | 246 | 6.0e-3 | 1.6e-1 | 1.8e-3 | 510 | 1.7e-3 | 1.3e-3 | 8.3e-5 | 855 | 9.8e-9 | 6.3e-8 | 3.5e-9 |
#表示时间步的数量。
从第一列可以看出,如果相对容差 太大,则较细化的网格无法减少误差,因此需要降低默认容差。我们还可以发现,当网格过于粗糙时,仅降低容差并不能减少误差。即使对于较小的容差,对于特定的网格尺寸,误差也会饱和。降低容差时,时间步的数量会增加(请注意,绝对容差与相对容差耦合)。在模拟过程中,耦合开始阶段时间步减小,之后略微增加直到结束。本例中,最大允许容差为 R= 0.0001。对于足够小的容差,误差大小取决于网格分辨率。请注意,更细的网格并不会使时间步数量更多。
我们进一步发现,通过将容差因子从 1 减小到 0.1,可以减少时间步的数量(未在表中显示)。原因是在此设置下,代数求解器的容差较低,并且代数误差对瞬态误差的扰动较小。从求解器日志中,我们还发现 BDF 阶数一直保持为5,直到模拟结束(否则,由于存在代数误差,它会减小)。总的测量误差与计算较少的时间步时相比,大致保持相同水平。该示例很好地证明了使用更严格的容差可以得到更有效的(更快的)时间步。当求解 PDE(偏微分方程)时,如何同时考虑空间和时间误差,这也是一个很好的示例。
此示例中,在 Tfail 或 NLfail 中没有记录任何失败,并且 BDF 阶数从 1 迅速增加到 5,并且之后在 2~5 变化(当容差因子未减小时)。对于这个简单的示例,代数求解器运行良好。即使此求解器使用了更费计算资源的雅可比更新策略(每次迭代),我们也可以从恒定(牛顿)切换为自动(牛顿)并获得相同的运行效果。但是,对于自动高度非线性(牛顿)求解器,我们发现 NLfail 会迅速增加,并且平均每两步就会出现失败。原因是该求解器使用了一个保守的阻尼因子,即使对于良性问题,通常也不会在 4 次迭代中收敛。可以看出,这些失败如何将时间步减少到 1e-5s 而不是 1e-3s 的说明(需要 100 倍以上的步长!)。这是时间步性能的急剧下降。我们可以通过将完全耦合求解器的最大迭代次数从 4 增加到 6(从而使代数求解器有机会完成工作)来解决非线性求解器的失败和较小的时间步。
如果选择阻尼因子 \omega=0.5,最大迭代次数 限制为 2 的恒定(牛顿),也能经常观察到非线性求解器的失败。我们发现,此时时间步长变得比以前更小。当容差系数 增加到 10 时,NLfail 和 Tfail 中有失败记录。打乱代数求解器可能看起来很奇怪,但是它说明了代数求解器设置不正确会破坏瞬态求解过程。当 \beta=0 时(一个线性问题),这些报错仍然存在。进一步增大容差因子 只会在 Tfail 中产生误差(代数求解器会接受较大的误差)。
情况2:NLfail 大于零
从求解器日志中,我们发现 NLfail > 0。
瞬态求解器在每个时间步求解代数问题(可能是非线性的)。每次代数求解器失败时,NLfail 列都会递增。用于代数迭代的雅可比行列式(或雅可比矩阵)的计算成本相对较高,因此,默认情况下极少对雅可比行列式进行重新评估(最小化雅可比行列式)。如果代数求解器不收敛,则时间步减少,重新计算雅可比行列式(雅可比矩阵),并再次求解代数问题,该过程非常耗费计算资源。需要注意的是,由于时间步是雅可比矩阵的一部分,因此采用最小化雅可比行列式 策略也会导致线性问题无法收敛。
如果由于时间步太大而导致代数求解器失败,并且重复发生,那么我们可以在时间步进 设置中启用非线性控制器 来改善这种情况,从而可以更保守地控制时间步,特别是对于高度非线性问题。
如果代数求解器失败,首先,我们可以增加最大迭代次数。其次,在每次迭代(或至少每个时间步一次)中将雅可比更新 变更为开。接着,再尝试不同的加速或增强方法。将安德森加速度(Anderson Acceleration)与分离代数求解器 结合使用将非常有效。如果可用内存允许,改用完全耦合 求解器可能效果会更好。对于完全耦合 求解器,降低恒定阻尼系数或使用自动 阻尼方法可能会有所帮助。
如果代数求解器仍然无法收敛,那么可以将求解器日志 更改为详细,从而获得各个因变量的误差估计(该功能自 COMSOL Multiphysics® 5.5 版开始)。此信息不仅会打印到日志视图,而且还会在单独的收敛图 窗口中显示。有了这些信息,我们就可以找出哪个变量在代数误差中起主导作用,使我们更深入地了解收敛问题。请注意,因变量的误差权重受缩放比例和该变量绝对容差选择的影响。
另一个直接影响代数求解器终止的重要参数是容差因子。数值1意味着代数问题的终止准则与局部时间步误差完全相同。一些物理场接口将此因子修改为较小的数。增加此因子可以更容易地实现收敛准则,但是同时存在代数误差扰动解的风险。因此,选择此因子时需要格外小心。
代数求解器的失败也可能是由线性求解器的失败引起的。线性求解器具有自动 错误检查机制,可防止代数求解器终止。如果“日志” 窗口中 LinErr 和/或 LinRes 列的数字不够小,可能会产生这个问题。为了验证实际情况,我们可以将线性求解器的检查误差估计 (误差 栏下)设置为 是。一旦存在无法在所需精度求解的线性矩阵问题,将停止时间步进并显示错误。
对于直接 线性求解器,我们可以尝试通过启用迭代求精(请参见直接线性求解器的错误栏)和 在非线性求解器中使用 选项来改善情况。对于迭代线性求解器,可以通过增加误差估计中 的因子 来简化终止准则,但是必须谨慎行事,否则会产生更多代数误差而扰动解。
对于迭代 线性求解器,请注意 LinErr 和 LinRes 的数值。如果这些数不够小,则可能存在预处理器无法精确求解矩阵的问题。首先,我们可以检查线性迭代求解器设置是否真正用于求解的矩阵,而不是尝试调整预条件器(使用显示默认求解器)。
示例:多匝线圈的磁场
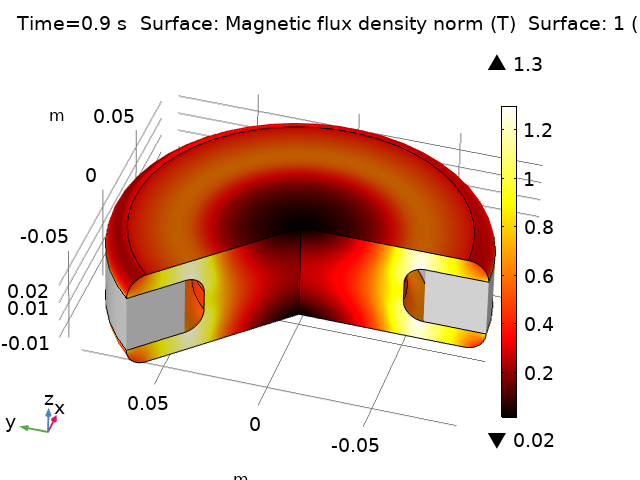
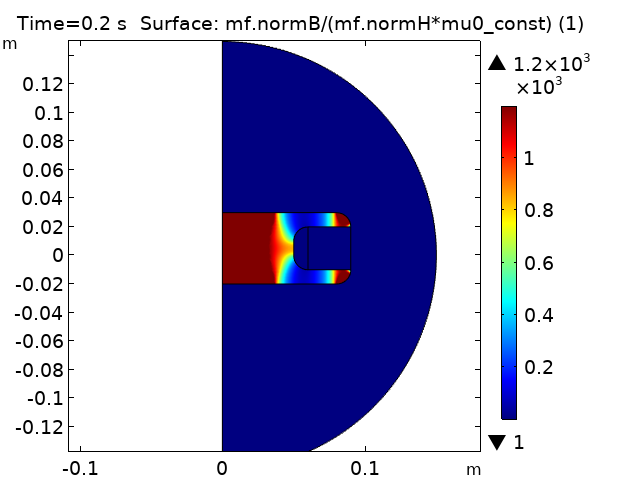
让我们使用带有二阶单元的“磁场”接口研究正弦电流激励的多匝铜线圈的时变磁场。示例铜线圈被空气包围,并由一个软铁片悬挂,该铁片具有非线性本构关系(非线性 B-H 曲线)。
将瞬态求解器的时间列表设置为 range(0,0.1,10),并将默认求解器设置为(完全耦合,恒定(牛顿),直接和最小雅可比更新),正弦线圈激励设置为 10A,我们发现,解扩展至5个周期(在时间为 10s 时结束)使用了大约 100 个时间步实现。需要注意的是,这种物理场的默认时间步方案使用中级作为求解器采取的步长设置。因此,根据指定的输出时间,将时间步长的上限设置为 0.1s。这可以通过检查求解器日志来查看。如果将激励增加到30 A,则需要降低输出时间的上限值(例如,总共需要约 200 个时间步至 0.05s),否则无法得到收敛解。
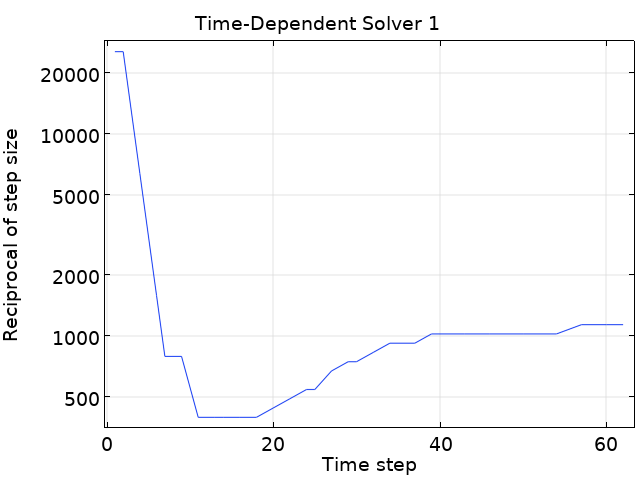
下面,让我们来详细地研究 40A 线圈激励的时间步轨迹。通过输出时间降低最大时间步约束的策略似乎没有效果(即使步长约束降低至 0.001s 也无效)。对于时间 设置为 range(0,0.05,10) 的情况,我们发现 NLfail 有很多失败,并且求解器在 109 个时间步后确实放弃计算,并显示了一条错误消息:
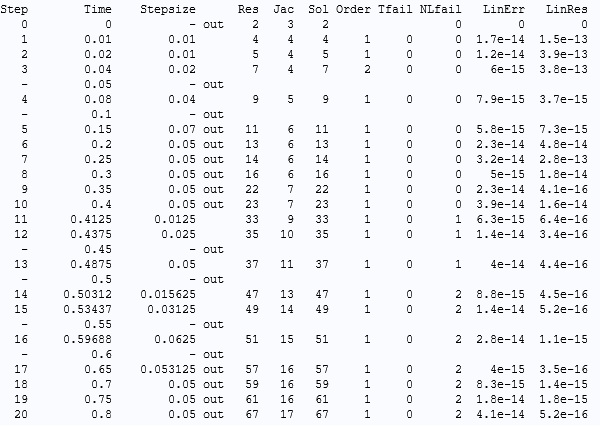
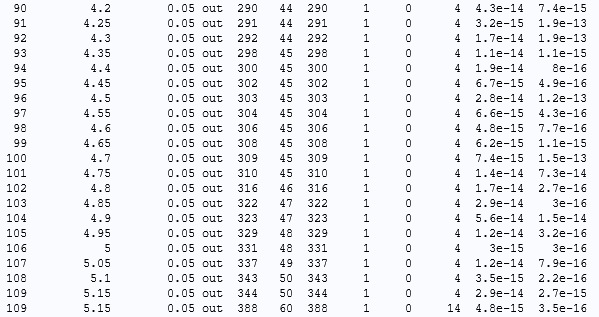
激励为 40A,输出间隔为 0.05s 时,多匝线圈模型磁场的求解器日志和默认设置。
我们可以在上图中最后一行找到失败的原因:10 次重复 NLfail。当出现 10 次错误后,求解器在进行下一步前放弃工作。此时,它已将时间步缩短 1/4 的工作重复了 10 次,对应的时间步缩小了 1,000,000 倍。此时,步长大小可能不是关键的问题。对于每次尝试,非线性求解器都不会在最大迭代次数内收敛。
我们正在模拟五个完整的线圈电流周期,即 10s。对于零线圈电流,矢势为零,因此我们需要仔细考虑比例。我们可以检查日志并看到磁矢势已自动设定为“1”。通过绘制求解器停止工作时的矢势,此时电流不为零交叉处,我们可以将磁矢势的量级估计为 1e-2 Wb/m。由于是根据解的范数,通过自动缩放的默认值来更新绝对容差,因此最好改为手动缩放矢势。
更改求解器设置的策略
按照上述情况 2 的建议,我们更改了求解器设置:
- 将磁矢势更改为“手动缩放”,更改为 1e-2。再次尝试,没有任何改善。
- 将完全耦合 求解器的最大迭代次数 更改为 10。再次尝试,没有任何改善。这似乎是一个非线性的问题。
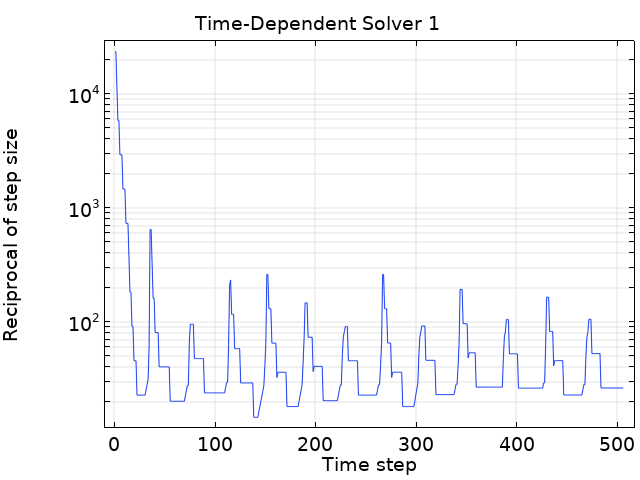
- 将雅可比更新 策略更改为每个时间步一次。再次尝试,我们发现在大约 200 个时间步内得到解,
NLfail没有报告任何失败(但我们仍然无法放开时间步限制)。 - 将雅可比更新 策略更改为在每次迭代。再次尝试,我们发现该措施确实有效!现在,即使使用
自由时间步进,我们也可以在 28 个时间步内完成求解(误差稍大,但误差估计仍满足规定的容差)。 - 接下来,我们需要问自己,采用中级 时间步进以及最大步长为 05s 时的结果是否准确。除了在零交叉处(t=0.5s 的倍数)矢势的计算值为 1e-16 Wb/m 外,矢量势的计算值约为 1e-2 Wb / m。因此,缩放比例似乎是正确的策略。复制上面的解以供参考,并用更严格的公差进行新的计算。
- 将研究中相对容差 更改为 0001,进行收敛性检查,注意相应的绝对容差也将减小。通过对缩小 100 倍容差的问题进行求解,我们对该模型进行了严格而良好的鲁棒性测试。大约需要 200 个时间步,并且代数迭代也要多 5%。
NLfail和Tfail没有出现失败。此计算结果与上述复制解的标称误差约为 1e-5 Wb/m,因此我们可以得出结论,时间离散具有较小的误差。本文未考虑空间误差。 - 激励为100 A时,即使求解器设置已经调整且最大时间步为 0.05s,中级 时间步进和和默认容差仍会产生误差小于1%的结果。
在该实验中,我们发现默认的求解器设置对于10A激励而言是完美的。如果打开激励,则非线性效应会更强。对于求解器而言,这是在低成本和鲁棒性之间进行权衡的问题。在非线性更强的情况下,我们必须手动提高鲁棒性。另一方面,在较低激励的情况下,设置更多的鲁棒性会降低性能。
情况3:Tfail 大于零
从求解器日志中,我们发现 Tfail > 0。
采用瞬态求解器得到时间步失败意味着不满足相对于容差的误差范围,并且需要以较小的时间步来重复计算。通过前面描述的机制确定新的时间步,对于每个失败,Tfail 列都会递增。这可以被视为时间步失败控制器,因为它不能正确预测局部误差的变化。
当务之急,我们应该缩小时间步并重新计算。如果是由于一个不容易预见的瞬态解(由于其非常瞬态的性质)而发生这种情况,则可能难以改进(在所采取的步骤中未加任何控制)。另一方面,如果这种情况定期发生且没有任何瞬态解,则存在改进的空间。
一个常见的原因是误差估计不平滑,因此其误差逐步变大。这可以通过低阶(使用 BDF 求解器)来证明。有时,降低相对容差 或 减小代数容差因子以减少代数错误是一种补救措施。求解PDE问题时,还可能是由于空间网格太粗糙。可以通过细化网格或引入更多的空间稳定性进行补救。此外,还有最后一种措施是改用“手动” 控制时间步进(这对于 Tfail 是不可能的,但是也没有误差控制)。进一步的选项包括使用较小的初始步长 或 在时间步 部分施加最大步长约束 。
NLfail 和 Tfail 还可能都增加。代数求解器的错误可能与时间步的选择机制错误有关。在这种情况下,代数求解器和时间步机制都应进行调整。但是,只有在问题解决得当的情况下,该策略才能成功,否则所有的措施都将无效。
示例:流体阻尼器
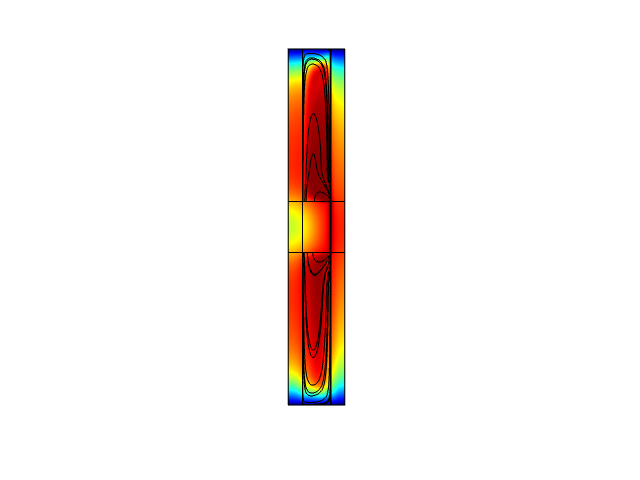
该流体阻尼器案例模型是一个阻隔冲击或抑制由地震和风力引起的震动的装置。该模型模拟了设备中的黏性加热现象。
该模型很好地演示了模拟过程中时间步如何变化。使用默认求解器设置,将记录多次 Tfail 失败。
让我们看看如何防止这些失败以及如何提高仿真性能。由于周期性的载荷,流体可以上下交替运动。这意味着速度和压力梯度场将改变方向并通过一个零交叉(在短时间内所有自由度)。在这种情况下,绝对容差的自动更新会导致复杂化,因为绝对容差将在转折点附近获得非常小的值。通过日志检查并将其与活塞的周期性位移进行比较,可以发现 Tfail 发生在这些点附近。另一方面,量级变化很大。
我们想到的第一个策略是:在“绝对容差”部分中的瞬态求解器上关闭更新缩放的绝对容差复选框。但这是行不通的。注意,在代数变量设置 部分,所述误差估计 被设置为排除代数 ,压力(comp1.p)容差因子 设定为 0.05。
我们尝试在“因变量”节点下的变量 节点上使用手动缩放。在“缩放比例”部分中将“方法”设置为“手动”,压力使用比例 1e7,温度 使用 1e2,速度 使用 1e1。另外,压力和温度的容差系数为 0.1,速度的容差系数为 0.5。此时,不会出现 TFail,但是出现了 6 个 NLFail。相比于原来的 1300 个时间步,该设置仅使用了约 400 个时间步。例如,通过将分离 节点上的最大迭代次数设置为 15,并将 Anderson 加速度的迭代空间维度 设置为 8,可以降低 NLFail。这些更改节约了大量计算时间。
示例:放大电路中的电感器
放大器电路中的电感器示例演示了如何将电路仿真与有限元仿真结合起来。这是一个通过调整容差因子 来优化时间步进方案的示例。在这种情况下,对于雅可比更新 ,具有最小设置的额外代数步进足以节省工作。使用存储在模型中的求解器设置,我们发现 170 步就可得到研究 2 的稳态和瞬态解,出现 10 个 TFail 和 1 个 NLfail。
通过将容差因子 降低到 0.1 并将最大迭代次数 增加到 6,我们发现步数减少为 127(出现 2 个 TFail 和 0 个 Nfail),而无需更改雅可比更新设置。其余的 Tfail 来自初始步长。也可以通过将初始步长降低到 1e-9s 来避免这些错误。但是,这样做效果不佳。对于此示例,可以使用更严格的容差来显著提高求解效率。
结论
本篇博客文章中,我们介绍了一些提高仿真效率的策略,包括在求解器设置中如何“旋转按钮”以及可以从瞬态求解器日志中获取什么信息。有关这些主题的更多内容,可以从 COMSOL 知识库中获取。
相关资源
阅读以下 COMSOL 知识库中的文章,了解更多相关信息:



评论 (11)
炳均 陈
2021-08-31在粒子追踪模块中模拟粒子飞行时间,区间为0到19300ns,当我减小时间步从9ns减小到1ns后,结果出现了不收敛。当我保持时间步为1ns,减小区间为0到1930ns后,结果收敛。请问如何保持区间0-19300ns,时间步为1ns?
现在的问题是,要么需要增加时间步,要么需要减小时间区间。如何维持较大的时间区间,并维持较小的时间步,并收敛呢?
王 刚
2021-09-01 COMSOL 员工具体情况具体分析,建议把模型发到 support@comsol.com,让工程师帮忙检查一下。
Jie Caleb
2022-05-26我也遇到了与楼上相同的问题,我的是等离子体介质阻挡气体放电模型,如何保证大的时间区间段,并且设置成较小的时间步呢?
洋洋 张
2022-05-26 COMSOL 员工可以展开求解器配置,点击瞬态求解器-时间步进,手动设置求解时间步长。参考链接:https://cn.comsol.com/support/knowledgebase/1254
Tong Xu
2023-12-15我的优化为什么只停留在2%,循环的计算,已经算了5小时
涵玉 徐
2023-09-24请问,就算产生了Tfails是不是没法说明这个瞬态求解是无法计算的?毕竟Tfails仅仅是自适应时间算法使用的步长没通过测试,再缩小一次步长罢了。
Qihang Lin
2023-09-25 COMSOL 员工您的理解正确,就算累积了Tfails也可继续计算,可能在缩小步长后得到收敛结果,可以继续算下去。
涵玉 徐
2023-09-27谢谢你
李托夫斯基
2024-02-19请问在情况3的流体阻尼器示例中,压力、温度和速度的缩放比例大小是由什么确定的呢?
越 赵
2024-03-05 COMSOL 员工您好,变量的缩放比例通常是根据该变量本身的数量级确认的,需要将较大的值缩放到1-10这个量级进行求解,详细可以参考:https://cn.comsol.com/support/knowledgebase/1240
明 赖
2025-02-14在进行电场和流场耦合过程分析流体流动粒子分析时,出现的报错“非线性求解器不收敛”,请问怎么去解决呢?