带标签的博客文章 CFD 模块
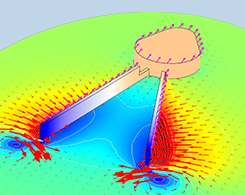
使用 COMSOL 模拟多体机构中的流-固耦合
要模拟高级FSI场景,如游泳机制或风力涡轮机叶片周围的气流,您可以使用流体-结构交互作用,配对多物理耦合。

仿真 App 助力 ABB 牵引电机公司实现数字化
下面是一个使用COMSOL Server™优化研发过程的真实例子:在ABB牵引电机公司,工程师们在电机设计中使用模拟应用程序来分析CFD和热量。

主题演讲视频:通过仿真优化电缆系统
电缆为高空飞机、地下矿井和海上风电场提供电力。根据使用情况,电缆的形状、尺寸和环境可能有很大不同——所有这些因素都会影响其性能。

主题演讲视频:EPFL 通过仿真拿下超级高铁大赛冠军
EPFLoop 团队凭借其设计的超级高铁舱站上了 COMSOL 用户年会 2018 洛桑站的领奖台,他们展示的方案让观众们大饱眼福。

介绍2种网格自适应方法——实现更高效的计算
网格自适应的目标是通过修改网格来实现更高效地求解。通常,我们希望使用尽可能少的网格单元来获得精确的解,以及在不太重要的区域使用较粗的网格,而在感兴趣的区域使用较精细的网格。有时,我们甚至可能会考虑各向异性单元。从 5.4 版本开始, COMSOL Multiphysics® 软件内置了一些增强方法以调整网格。今天,让我们来看看在 COMSOL 软件中,如何使用网格自适应方法实现更高效的计算。 确定所需网格单元的大小 要调整网格,我们必须知道实际所需的网格单元大小。但是,在实际工作中需要进行大量的研究才能找到合适的单元尺寸。对于稳态和特征值问题,我们可以使用COMSOL Multiphysics 中的自适应和误差估计功能,基于内置的误差估计自动调整网格。 在COMSOL 软件中,网格自适应方法不仅局限于进行误差估计,还可以更加灵活地应用。比如,我们可以先在粗网格上求解一个较简单的问题,然后基于此解,通过计算的表达式来控制一个较难问题的单元尺寸。另外,还可以使用导入的插值函数或自定义的任何函数。 本文不涉及这方面内容,而是假设已经隐式或显式地知道所需的单元大小是 x,y 和(在 3D 中)z 的函数。这意味着一个网格单元的边长由该边中点坐标的函数表达式确定。通常,不可能完全满足此要求,即使是一个三角形也需要满足三角形不等式。但是,请记住:大小表达式表示空间中每个点上所需的单元边长。 根据大小表达式调整网格的 2 种方法 在 COMSOL Multiphysics 中的 网格节点,可以通过2 种不同的方法来构建适应大小表达式的网格。 第一种方法,我们可以在网格划分序列中使用大小表达式 属性来改变生成网格的大小。如果使用研究中的网格自适应功能,则相当于选择了 重建网格 选项,其中的自由网格生成器(自由三角形网格,自由四边形网格和自由四面体网格)会考虑这个大小。另一方面,结构化方法(例如映射 和扫掠,和某种程度上的边界层)会忽略大小表达式属性(根据定义,结构化网格不能遵循大小可变的字段)。简单来说,就是如果我们构建的是结构化网格,可能无法使用此方法。 另一种方法是使用 自适应 操作。此操作通过单元细化和粗化来修改现有的网格。我们可以在具有任何单元类型的网格上以及在导入的网格上使用自适应操作。这是一种更强大的方法,并且能够更好地遵循指定的大小表达式。但是,结果通常不如从头开始生成的网格平滑。 下面,我们将详细讨论这两种方法,看看结果有何不同。 使用大小表达式属性 如前所述,使用大小表达式属性方法通常能获得高质量的网格。但是,如果它产生的单元质量较差,则可能不遵守所需的大小(例如,进行快速大小转换时)。有关网格质量的讨论,请阅读 COMSOL 博客文章:如何检查 COMSOL Multiphysics® 中的网格。由于网格在每一次适应时是从零开始构建的,因此对于复杂的几何形状而言,此过程可能很耗时。 使用大小表达式属性对圆形几何的三角形网格应用一个表达式,结果具有高质量的网格单元和平滑的尺寸过渡。 如果我们具有已知的大小表达式(例如,全局插值函数),则在背景栅格上进行计算通常会很方便(在上图中的栅格基础上计算)。我们需要确保栅格分辨率足够高以捕获大小表达式描述的所有特征。 当大小表达式取决于已知的空间变化量(例如材料)时,我们可以使用初始表达式计算选项。之后,可以使用模型中的任何表达式。软件将会在求解前计算表达式(对应于获取求解步骤的初始值命令,可用于研究步骤)。我们还可以指定某个研究步,因为一些表达式的值取决于研究。 最后,我们还可以在现有解上计算。表达式类型为错误指示器 用于内置错误估计,但我们也可以使用任何大小表达式——这可能依赖于现有的解。例如,我们可能想在应力较大的地方细化网格。 使用自适应操作 另一种方法是基于现有的网格进行修改以匹配所需的单元大小。这就是自适应 操作的作用。它适用于所有尺寸,也可作用于导入的网格。它的许多选项和输入字段与大小表达式 属性相同。 该操作有三种适应方法:最长边细化,常规细化 和通用修改。两种细化方法是基于单元边的二等分法,由于这些单元边太长,保留了所有现有的网格顶点,因此这些方法无法粗化网格。 自 5.4 版本开始,COMSOL Multiphysics 软件内置了通用修改 方法。顾名思义,就是以非常通用的方式修改网格: 单元可以被细化 如果网格太细,可以通过删除顶点来粗化网格 可以通过单元修改,移动网格顶点来提高网格质量 使用自适应操作的通用修改方法,对 大小表达式属性应用同一表达式。虽然对于大多数应用而言,网格单元质量足够高,但是大小过渡不如从头开始生成的网格平滑。 如果将适应方法更改为最长边细化,结果如下图所示。将太长的边一分为二,直到网格被充分细化。此网格操作非常快,但是即使输入网格的质量很高,该方法通常会产生低质量网格单元。 与上述模型相同,但是将自适应方法设置为 最长边细化。这里,我们可以看到原始三角形形状产生的图案。 支持所有单元类型 自适应 操作可用于所有单元类型的网格,也可以作用于结构化网格域(虽然,网格自适应后通常不再是结构化)。但是,当在复杂单元(二维中的四边形,三维中的六面体、棱柱、锥形)中使用此方法时,我们必须要小心,因为结果可能很差。下面,我们来看看在这种情况下单元尺寸大小是如何过渡的。在二维模型中,将三角形插入到四边形网格中。 左:圆形几何中默认的自由四边形网格。以最大角度质量对单元进行着色。右:网格适应为与上面相同的大小表达式后的结果。请注意在尺寸过渡区域中三角形是如何使用的。 在三维结构中,通常将四面体和锥体用于尺寸过渡区域,在合适时也可以插入其他单元类型。下图显示了具有粗糙六面体网格的圆柱体,该圆柱体使用 0.02 + z*z 表达式进行适应。 适应前后的圆柱体网格。 […]

模拟含低渗透性晶体的多孔介质中的多相流
建立相输运模型有助于研究多孔介质中的多相流(如地下水通过土壤)。

使用激波管仿真 App 研究激波现象
冲击波过去只是一个理论问题。 然后,冲击管使实验成为可能,但它既昂贵又低效。

主题演讲视频:仿真助力心脏泵设计改进
心力衰竭是一个全球性的健康问题,影响着数百万人,使他们无法正常生活。但是,如果有一种装置可以让患者的心脏保持跳动,甚至提高他们的生活质量,将会怎样呢?
