带标签的博客文章 技术资料

如何在求解模型后使用作业序列保存数据
2025年 4月 24日
这篇博客可以指导用户如何在求解模型后,自动化常见任务。阅读博客,了解如何使用作业序列功能。

模型求解完成后如何自动导出图像
2025年 4月 23日
你知道 COMSOL Multiphysics® 可以在模型求解完成后自动导出结果图像和动画吗?点击此处,了解详情。

如何导入图像并放样成实体
2025年 3月 21日
假设你想模拟一个不规则的形状,比如人类的头部。如何建立几何图形呢?在这篇博客中,我们将介绍如何通过导入图像和放样实体来实现这一点。

提升带通滤波器器件仿真效率的方法
2024年 7月 18日
在频域中使用有限元法设计具有高 Q 值的带通滤波器类型的器件时,可使用本篇博客中介绍的一些方法来提升仿真效率。
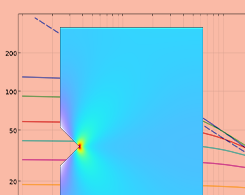
如何评估奇异应力场?
2024年 3月 21日
探讨奇异应力场的性质,并了解在 COMSOL Multiphysics® 中使用的一些可能的计算方法。

复合材料模块简介
2024年 1月 24日
阅读这篇博客,探索复合材料模块,一个包含模拟层状复合结构的专用功能的COMSOL Multiphysics®附加产品。
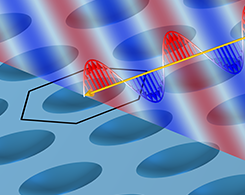
理解高阶衍射
2024年 1月 9日
探索如何使用埃瓦尔德球来研究平面周期性结构的衍射。(亲自动手实践案例模型,获得完整的图片!)

批处理扫描功能的优势
2023年 5月 19日
你有没有过通宵运行大量参数化扫描,第二天早上发现仍未完成求解的经历?在等待最后几个参数收敛的时候,你可能希望先查看已经计算出的参数解。
