当电磁辐射平面波(例如光)入射到平面周期性结构上时,可能会发生高阶衍射。根据斯涅耳定律,光不仅会发生反射和折射,也能散射到多个不同的方向,这种现象称为衍射级。我们使用几何方法可以知道什么时候会出现衍射级,以及光会散射到哪些方向。接下来,让我们了解更多详细内容。
理解平面周期性结构的衍射
我们以入射到具有无限周期的平面结构上的平面光波为例来说明。该平面上方和下方的介质可以具有不同的折射率,并假定为无损耗和无限域。在这些介质的交界面,存在材料性质和形状等复杂的周期性结构。入射到周期性结构上的光至少会发生镜面反射,也会发生折射(称为镜面透射),通常还会有一些损耗,因为电磁能会转化为热能。反射角和折射角可以通过斯涅尔定律计算,但入射光在周期性结构中的反射、透射或损耗的部分需要进行数值分析。
以一定角度入射到平面周期性结构上的平面波。突出显示了周期性结构的一个基本单元。
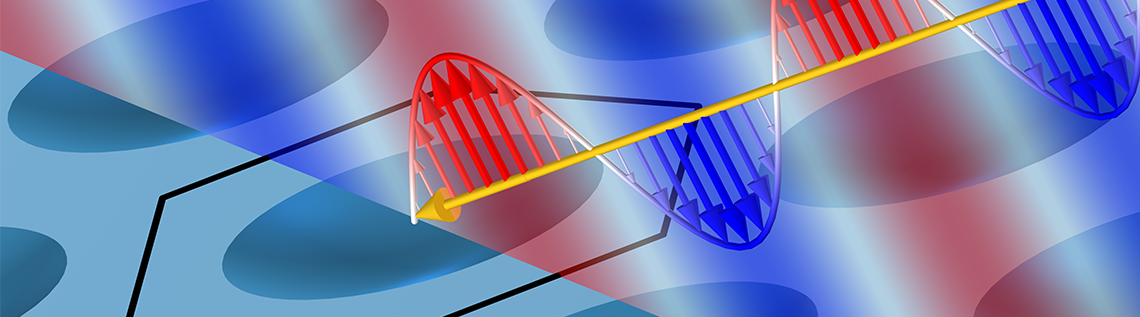
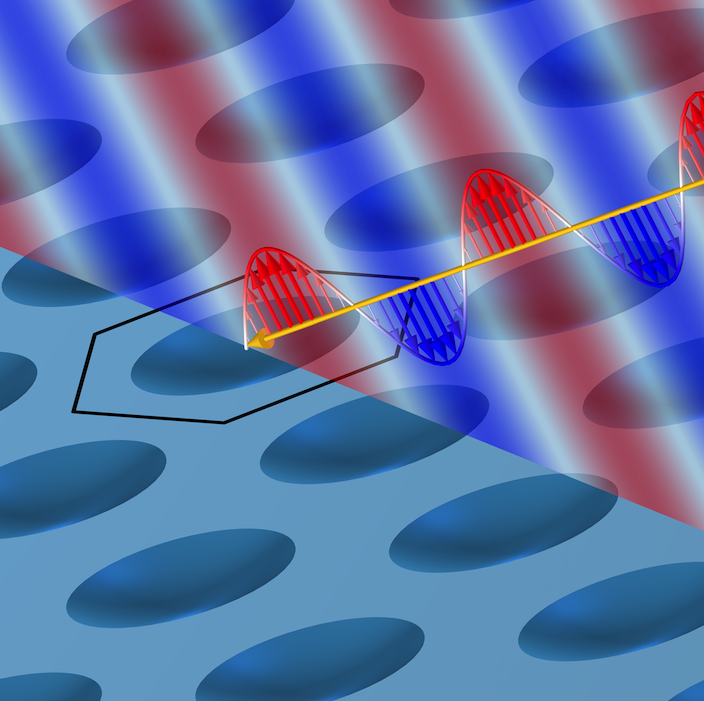
如前所述,也存在高阶衍射的可能性。当周期性结构散射的光被相长干涉到不同的方向时,就会出现这种情况。下面展示了这种结果的一个示例。
入射到周期性基本单元的线性偏振平面波(黄色)示意图。在反射(红色)和透射(蓝色)中,入射光被散射成几个不同强度和偏振的衍射级。
要确定这些进入其他相似方向的光的比例,同样需要建立一个数值模型,但要了解光会散射到哪些方向,可以通过一种被称为埃瓦尔德球结构的纯几何方法来实现。在开始数值分析之前,熟悉这种方法很有帮助,这也是我们将在这篇博客中介绍的内容。埃瓦尔德球几何结构既可用于单向周期性平面结构,也可用于面内双向周期性结构。
单向周期性结构
像光栅这样的平面周期性结构仅在一个方向上具有周期性变化,即该结构沿三维方向没有变化。当入射光在三维空间的法线平面上传播时,模拟可以被简化为沿一个方向具有周期性的二维平面。
以一定角度入射到单向周期性结构上的平面波,在结构或场中沿面外方向没有变化。突出显示了一个基本单元。
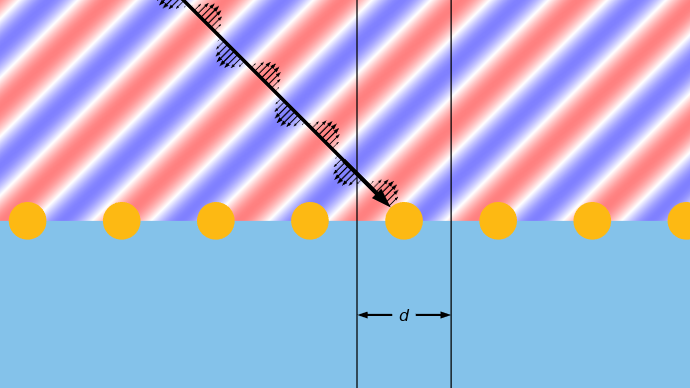
对于这些结构,我们只需考虑基本单元间距 d,并首先在 倒易空间中绘制一组晶格点,因此下图中的尺寸单位为逆长度。这些晶格点的连线对应于周期性结构的界面平面。晶格点之间的间距为 2\pi/d,晶格点的索引从第四个晶格点 m=0 开始,可将其视作位于基本单元的中间。然后,在晶格点连线的上方和下方绘制两个半圆。反射侧的半径为 n_{r}2\pi/\lambda_{0} ,透射侧的半径为 n_{t}2\pi/\lambda_{0},两侧的折射率分别为 n_{r} 和 n_{t},\lambda_{0} 为自由空间波长。对于与法线夹角为 \theta_{inc} 的入射光,这些圆的公共中心与晶格的第零个点偏移了 sin(\theta_{inc})n_{r}2\pi/\lambda_{0}。位于这些半圆内的晶格点对应于可能的衍射级。
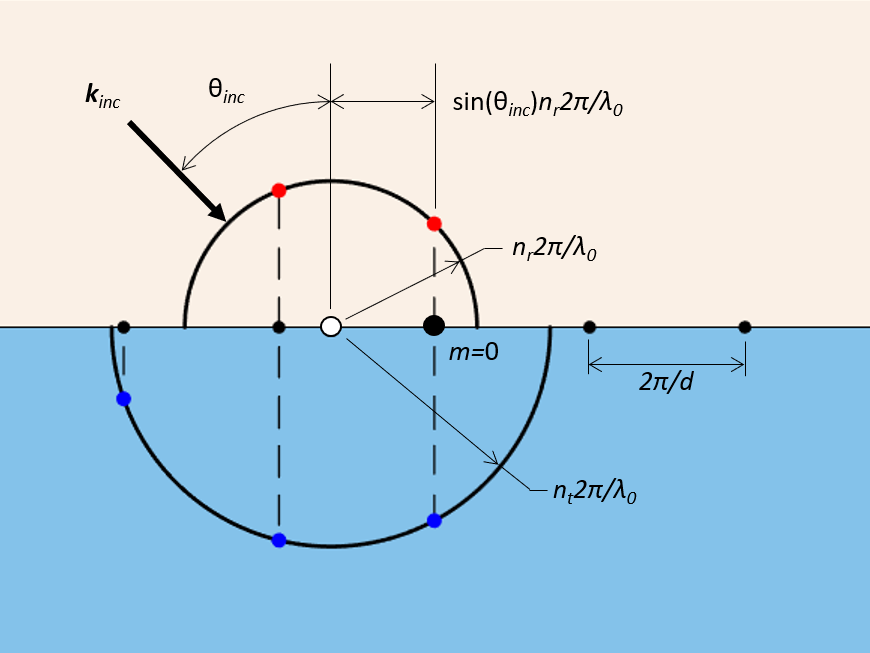
用于确定单向周期性平面结构的衍射级的几何结构,该平面结构被一定角度入射的平面波照射。请注意半圆(白点)的中心是如何偏离第零晶格点的。
这种结构还可用于确定衍射的方向,并为每个方向分配一个索引。从半圆中心投影到晶格点的矢量对应于每个衍射级的 \textbf{k} 矢量。这些晶格点的索引在两侧的符号相反。指向第零个晶格点的箭头始终存在,代表镜面反射和透射。其他衍射级的存在取决于波长、折射率、间距和入射角度。COMSOL案例库中包含两个建立此类模型的案例:使用 RF 模块的表面等离激元线光栅(RF)和使用波动光学模块的表面等离激元线光栅分析仪(波动光学)。
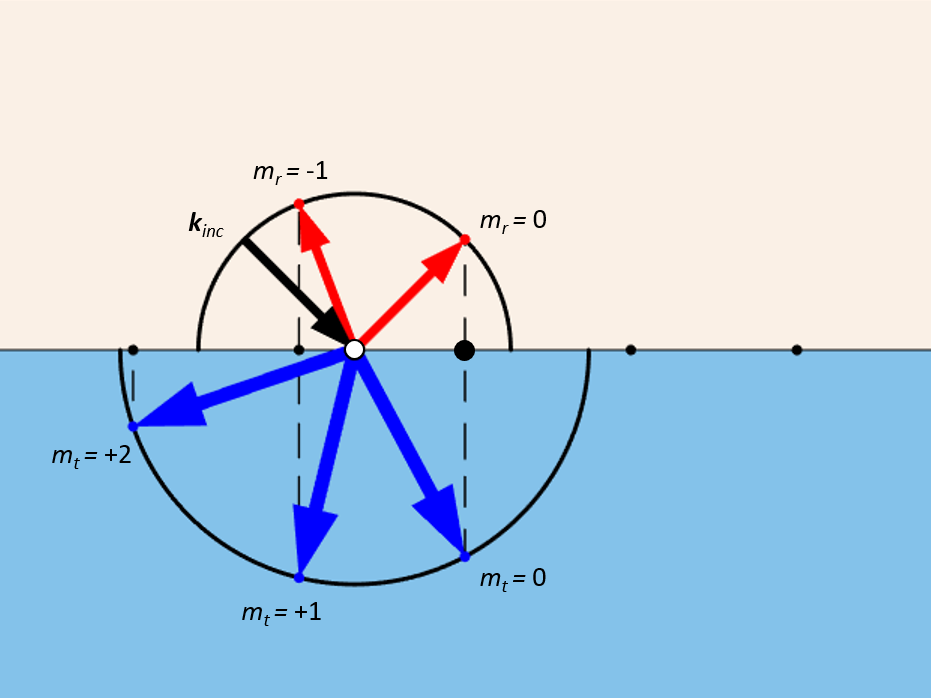
单向周期性平面结构各种衍射级的波矢量。请注意反射衍射级与透射衍射级之间索引符号的变换。
双向周期性结构
现在,我们来看看在两个方向上具有周期性的平面结构的衍射情况。下图显示了构建平面的矩形、菱形和六边形基本单元。这些单元由两个单元矢量定义:\textbf{a}_{1} 和 \textbf{a}_{2},它们从一个点开始,沿着相邻的边到达下一个顶点。虽然我们可以自由使用任何坐标和方向,但本文将始终选择 \textbf{a}_{1} 向量与全局笛卡尔 x 轴对齐,并始终从光照方向俯视基本单元。此外,还有两个基向量 \textbf{b}_{1} 和 \textbf{b}_{2},描述了基本单元在平面上的移动方式,用于构建平面。也就是说,要构建整个平面,需要在 m\textbf{b}_{1}+n\textbf{b}_{2} 的基础上复制基本单元,而 m 和 n 的值可以是任意整数。这两个矢量的叉积大小可用于计算基本单元的面积:A_{c} = ||\textbf{b}_{1}\times\textbf{b}_{2}||。

矩形、菱形和六边形基本单元构成了二维平面。单元矢量与单元的两条边相对应,而基矢量则描述了如何移动单元来构建平面。
这些基矢量用于定义两个倒易空间衍射矢量:\textbf{d}_{1} = 2\pi(\textbf{b}_{2} \times \textbf{n})/A_{c} 和 \textbf{d}_{2} = 2\pi(\textbf{n} \times \textbf{b}_{1})/A_{c},其中\textbf{n} = (\textbf{b}_{1} \times \textbf{b}_{2})/A_{c} 是周期性平面的法向量,即 +z 轴。这些衍射矢量与基矢量垂直,并通过取整数和在周期性平面上创建衍射晶格:m\textbf{d}_1+n\textbf{d}_2,晶格中的每个点对应于 \textbf{d}_{1} 和 \textbf{d}_{2} 方向上 m 和 n 的索引对。在基本单元的传输侧,点的位置相同,但索引调换,且符号相反。
现在,我们可以在三维空间的周期性平面上将这些衍射点可视化,并在平面上方和下方添加一个半径等于材料中波矢量的半球。通过半球,我们可以得知在反射和透射中存在哪些衍射级。刚开始,我们以点 m = 0, n = 0 为半球中心,代表法向入射光线。
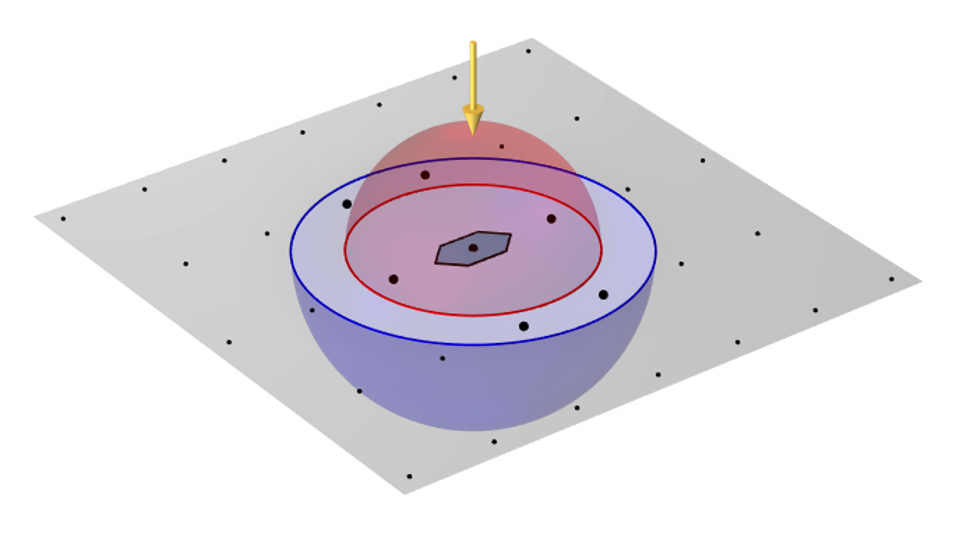
平面波光(黄色箭头)通常入射到一个周期性六边形单元上。衍射点绘制在周期性平面上,位于反射半球和透射半球内的突出点表示将出现的衍射级。
接下来,我们来看看入射仰角和入射方位角变化时的情况。考虑到我们习惯上选择保持 \textbf{a}_{1} 向量与球坐标的 +x 轴对齐,增大入射仰角意味着入射波矢量首先绕 –y 轴旋转;然后,入射方位角增大,入射波矢量随之绕 +z 轴旋转。因此,入射仰角从 0^{\circ} \le \alpha_{1} < 90^{\circ} 开始,入射方位角从 0^{\circ} \le \alpha_{2} < 360^{\circ} 开始,如下图所示。入射波矢量和周期性平面的法线定义了入射平面。当光从法线入射:\alpha_{1} = 0^{\circ}, \alpha_{2} = 0^{\circ},入射平面被定义为 xz 平面。

入射仰角和入射方位角表示入射波矢量(黄色)的一系列连续旋转,先是绕 –y 轴旋转,然后绕 +z 轴旋转。图中也显式了入射平面。
入射角的变化改变了半球中心的位置。从半球中心到 m = 0, n = 0 点的倒易空间距离为 k_{r} = \text{sin(}\alpha_{1}\text{)}2π/ \lambda_r,该位置在平面内的移动量为 k_{x} = -k_{r}\text{cos(}\alpha_{2}\text{)} 和 k_{y} = -k_{r}\text{sin(}\alpha_{2}\text{)},如下图所示。因此,仰角和方位角的变化往往会导致出现不同的衍射级。
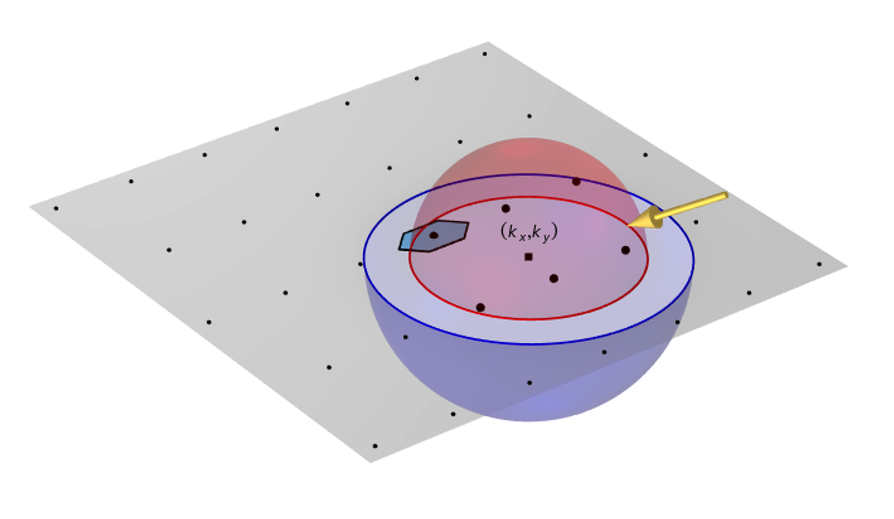
以非零仰角和方位角入射的平面波光会移动半球的中心,从而产生不同的衍射级。
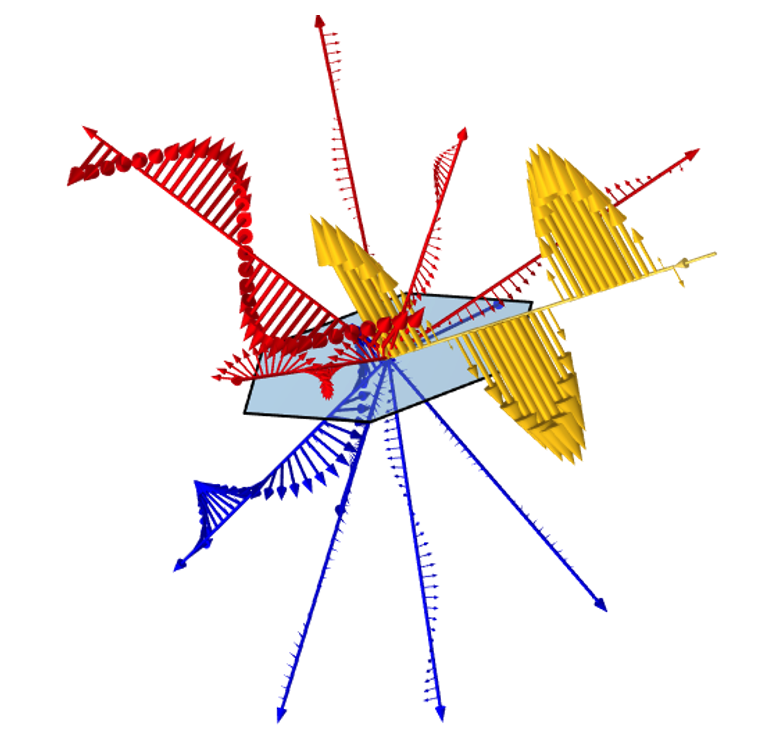
通过这些半球,我们还引导每个衍射级的波矢量。将衍射级点投影到半球上,会得到另一组点,而每个衍射级的波矢量等于从半球中心到这些投影点的矢量。
将衍射点投影到半球上,就得到了每个衍射级的波矢量。这种几何结构说明了入射光(黄色)在反射(红色)和透射(蓝色)时将衍射到哪个方向。您可以使用鼠标与此三维模型进行交互:左键单击旋转,右键单击平移,滚轮滚动缩放。
最后,通过这些矢量,我们还可以知道偏振状态。对于每个衍射级,偏振状态都会根据琼斯矢量的面内和面外分量表示。每个衍射级的平面都是波矢量和周期性平面的法矢量所描述的平面。对于所有衍射级,琼斯矢量的面外分量对应于电场平行于周期平面的波。
衍射级方向描述了一组平面,用于定义每个衍射级的偏振状态。突出显示了入射面和一个衍射级。您可以使用鼠标与该三维模型进行交互:左键单击旋转,右键单击平移,滚轮滚动缩放。
结论
综上所述,我们可以得出以下结论:使用埃瓦尔德球的几何构造可以理解平面性周期结构衍射,并且能够得知在反射和透射中会出现哪些较高的衍射级。我们还可以得知波矢量以及用于定义琼斯矢量方向的平面集。在求解数值模型时,会自动得到这些信息,因此这种几何构造并不是必须的,但它有助于我们建立理解和直觉。
进阶学习
如果您想学习高阶衍射建模,下面的示例模型是很好的起点,这些模型可以使用 RF 模块或波动光模块建立。
- 使用RF模块建立的模型:
- 使用波动光学模块建立的模型:



评论 (4)
海祺 张
2025-04-07请问COMSOL软件中可以忽略高阶衍射吗?
子奇 陈
2025-04-17 COMSOL 员工计算中不可忽略,后处理中可忽略。
海祺 张
2025-04-17后处理中该如何忽略呢
子奇 陈
2025-04-21 COMSOL 员工直接在绘图或者派生值计算中,选取所需的衍射级即可,其余没选择的不就是忽略了。