网格 博客文章
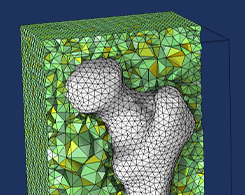
如何基于扫描图像数据创建和优化网格
2023年 4月 21日
你可以用 COMSOL Multiphysics® 中的 3D 数据创建仿真网格。这个功能在建模不规则形状时会派上用场。
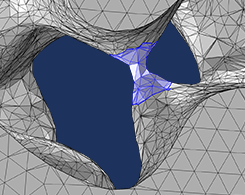
在 COMSOL Multiphysics® 中编辑和修复导入的网格
2022年 7月 19日
COMSOL Multiphysics®包括几种修改导入表面网格的操作。您可以创建、相交、分割和连接实体,调整和细化网格单元,等等。

如何检查 COMSOL Multiphysics® 中的网格质量?
2022年 7月 6日
您正在剖分模型的网格,突然跳出一条警告或错误。您应该如何解决它呢?一个选项是检查报告中列出的实体对象,进而分析并解决网格剖分问题。

三维感应加热模型的高效网格划分策略
2021年 5月 11日
您对三维感应加热模型的高效网格划分策略感兴趣吗?在这篇博客中,我们将演示如何根据单元类型划分网格。
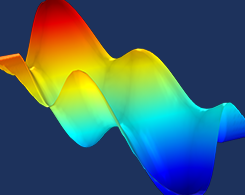
如何将点云数据转换为曲面和实体
2021年 1月 28日
在实际仿真过程中,并不是所有分析都是以 CAD 模型开始的。有时,我们唯一可用的数据仅是一系列点数据,也称为点云数据。在这篇博客中,我们将演示如何将点云数据转换为可在 COMSOL Multiphysics® 软件中进行仿真分析的几何模型。

如何优化和调整导入的网格
2019年 8月 15日
2 项功能可最大程度地利用导入的网格: 1. 精炼操作可快速减小单元尺寸。 2. Adapt 操作通过表达式修改元素大小。
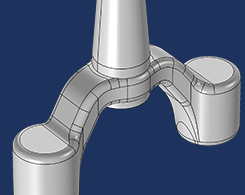
如何自动移除模型几何结构中的小细节
2019年 7月 12日
在 COMSOL Multiphysics® 软件中设置仿真时,你有时可能希望用自动方法来移除几何结构中一些能产生不必要的细化网格或质量较差网格的细节。
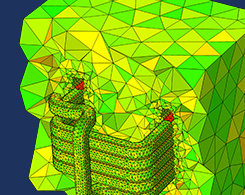
使用不同尺寸设置进行网格划分的最佳方式
2019年 7月 9日
提示 1:选择网格划分序列操作的顺序。提示 2:使用单个操作对多个域进行网格划分。请继续阅读全文了解如何确保模型域的高质量网格划分。
