几何 博客文章

如何导入图像并放样成实体
2025年 3月 21日
假设你想模拟一个不规则的形状,比如人类的头部。如何建立几何图形呢?在这篇博客中,我们将介绍如何通过导入图像和放样实体来实现这一点。

新课程:在 COMSOL Multiphysics® 中构建几何
2024年 1月 29日
阅读文章,探索在 COMSOL Multiphysics® 中构建简单和复杂几何的学习中心课程介绍。
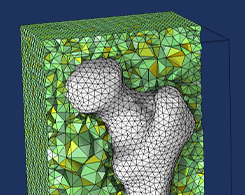
如何基于扫描图像数据创建和优化网格
2023年 4月 21日
你可以用 COMSOL Multiphysics® 中的 3D 数据创建仿真网格。这个功能在建模不规则形状时会派上用场。
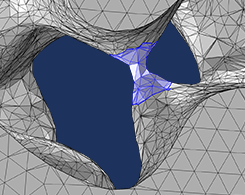
在 COMSOL Multiphysics® 中编辑和修复导入的网格
2022年 7月 19日
COMSOL Multiphysics®包括几种修改导入表面网格的操作。您可以创建、相交、分割和连接实体,调整和细化网格单元,等等。

如何对卷绕和翘曲几何形状进行建模?
2021年 9月 10日
CAD 零件通常设计为未变形的制造状态。 然而,当谈到分析时,我们只对变形的组装状态感兴趣。
如何将点云数据转换为曲面和实体
2021年 1月 28日
在实际仿真过程中,并不是所有分析都是以 CAD 模型开始的。有时,我们唯一可用的数据仅是一系列点数据,也称为点云数据。在这篇博客中,我们将演示如何将点云数据转换为可在 COMSOL Multiphysics® 软件中进行仿真分析的几何模型。
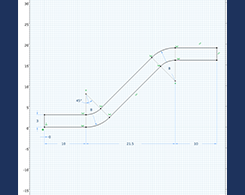
如何在 COMSOL®中使用草图工具绘制二维几何
2020年 6月 18日
在COMSOL软件中对二维组件进行建模,或在三维模拟中使用工作平面时,您可能已经注意到,如何创建几何图形的功能发生了一些细微但重要的变化。使用草图 模式以及约束和尺寸,可以绘制平面几何图形并定义您所绘制的几何实体之间的关系。
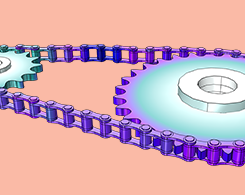
在多体动力学模块中创建滚子链的几何形状
2020年 2月 13日
COMSOL Multiphysics® 软件为您提供了链传动系统建模的便捷方法。本文为链传动建模系列博客的第一部分内容。在本篇博文中,您将了解如何使用 COMSOL Multiphysics 零件库中的内置参数化几何零件创建滚子链组件的真实几何模型。
