使用不连续网格模拟共轭传热

你是否知道 COMSOL Multiphysics^® 软件允许在相邻域中使用不同的不连续网格？尽管 COMSOL 软件通常默认使用连续对齐的网格，但是有时我们可能希望使用不连续的网格，例如用于模拟共轭传热。本篇博客，我们将对这个主题进行更深入地研究，了解如何在初始模型开发中使用这些网格更好地节省时间和内存。

保持场的连续性，平衡对齐单元之间的通量

有限元方法（FEM）的基本理论已经被讨论了好多次，例如在关于弱形式的博客文章中做过介绍，因此这里我们不再赘述。今天，我们将回顾一个关键问题：不同有限元之间的边界会发生什么？简单回答，就是当使用标准 FEM 时，相邻的对齐单元共享相同的节点（问题求解节点）。由于这些单元共享节点，因此要求解的场（例如温度场、固体位移场和流体速度场等）是自动连续的。

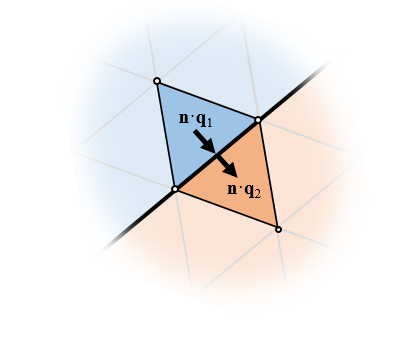
不同域单元之间的通量是自动平衡的，而且这些单元共享相同的节点，因此场是连续的。

此外，通量是相等的（尽管这需要对 FEM 的推导有更透彻的了解）。这里，术语通量 可以指不同的物理量，具体取决于我们正在研究的物理场。为了简便起见，我们仅考虑传热，也就是我们常说的热通量 ，以热导率乘以温度场梯度的负值来表示，或者 \mathbf{q} = -k \nabla T。在单元之间的边界处，FEM 自动（即不需要任何用户输入或其他内部方程式）使以下条件满足：\mathbf{n \cdot q_1 =n \cdot q_2 }，其中，\mathbf{n} 是单元之间边界的法线向量。就是说，标准的有限元法自动满足了场的连续性并且平衡了通量。但请记住，无论如何，我们始终需要进行网格细化研究，以确保模型的整体准确性。

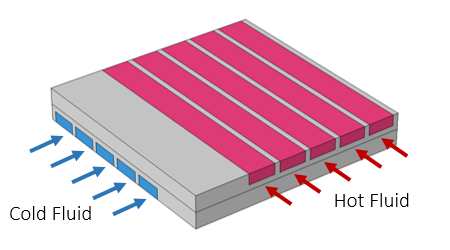
错流式换热器子模型示意图。

现在，我们来看一个 COMSOL 案例库中的示例模型错流式换热器，如上图所示。这是一个由直的矩形通道组成的较大型换热器的子模型，模拟了流经通道的流体，以及流体和周围固体中的温度场。温度场仿真结果如下图所示，同时绘制了沿着流动通道长度的代表线的温度。从这些图中可以看出，沿流动通道的温度变化随长度变化很慢，在流动通道的横截面上变化很快，并且穿过金属零件的过程非常复杂。

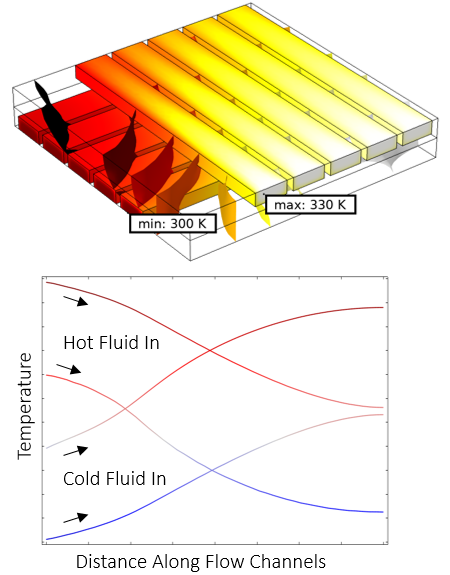
壁的温度场和固体中的温度等值面（顶部），以及沿流动通道方向的温度图（底部）。

下图为绘制的网格。我们可以看到网格在流体域和固体域之间是连续的。网格主要由四面体单元组成，在通道壁的流体侧施加边界层网格，以求解壁附近的高速度梯度和温度梯度。

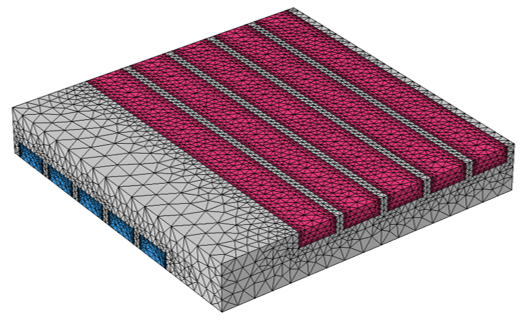
错流式换热器的默认网格在流体和固体之间是连续的。

现在，该默认网格自动生成，无用户干预。但是，如果我们想手动构建网格，如何允许网格不连续呢？这时该怎么办？在开始实现之前，让我们先看一下软件需要做什么。

保持场的连续性，并平衡未对齐单元之间的通量

假设我们在两个相邻域上有一组单元，如下图所示。单元具有相邻边界，但节点未对齐。使用形成装配体最终几何图形步骤时，会自动生成这种网格。分离对象的网格将不会连接，因此，跨越此边界的场将是不连续的，并且域之间没有通量。

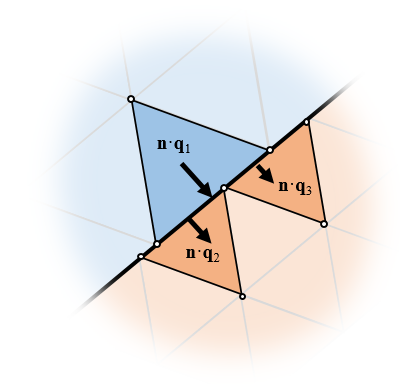
对于未对齐网格，必须引入额外的方程以大致平衡通量和场。

但是，形成装配 操作还可以在对象之间的相邻边界处自动创建所谓的一致对。然后，我们可以在每个物理场中将边界条件应用于这些边界对。根据物理场的不同，将提供不同的边界条件。但在所有情况下，对连续性 条件均可用。此条件以单元平均的方式强制执行跨边界的场和通量的连续性，这是通过在后台添加一组额外的方程式来实现的，我们在这里不再赘述。由于单元未完全对齐，因此场和通量不能逐点连续，这是一个缺点。但是，我们现在可以在相邻域中使用不同的网格，这是一个优点。让我们看一下在错流式换热器示例中，单元未对齐如何对我们产生正向的作用。

正如我们前面所看到的，沿流动通道的温度变化是逐渐变化的。由于流动是层流，并且通道的横截面是均匀的，因此流场沿流动方向几乎不变。我们可以沿流动方向在通道中应用扫掠网格，如下图所示。我们可以观察到，与之前的网格相比，在流动方向上使用的单元要少得多，从而仅通过较小的精度损失就可以降低问题的大小。

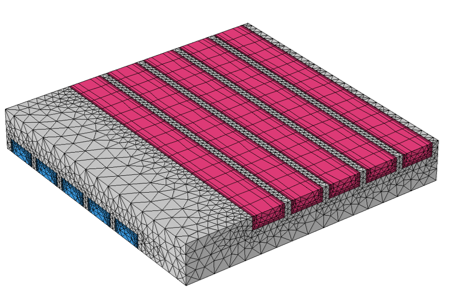
通过装配网格划分，流体通道中的扫掠网格允许使用较少单元的细长网格。

现在，我们需要一些其他手动步骤来设置此网格。首先，在几何 序列中，我们必须定义两个不同的对象。第一个对象是金属零件，即流体流经的固体。第二个对象是所有流体流域的组合。即，由若干不同的域组成的单个对象，这些对象是在几何序列通过布尔并集 操作创建的。我们需要确保这些域不重叠，以使最终操作形成装配体 有效，然后软件将自动识别这些对象之间的匹配面为一致对。

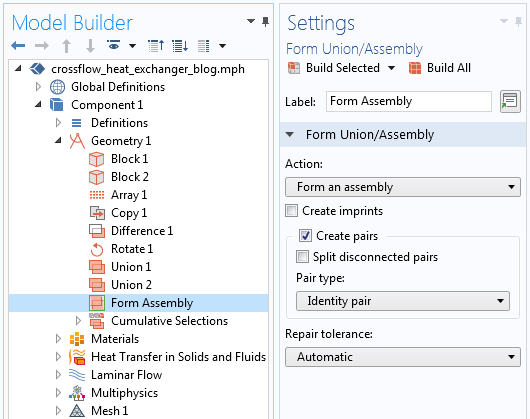
形成装配体几何完成操作自动创建一致对

接下来，在固体和流体 的 传热 接口中，我们需要添加 对连续性 边界条件。由于我们只有两个相邻的对象（实体域和所有流体域），因此仅需应用一个一致边界对，无需对物理进行任何其他更改。

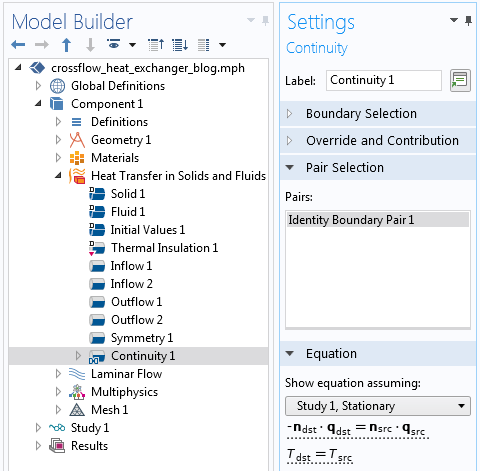
“对连续性”边界条件，强制场的连续性并平衡通量。

最后，我们还必须手动修改网格 序列。默认的网格划分序列会复制一致对边界的匹配面上的单元，但我们要禁用此功能，并应用一个沿流动通道的长度拉长的扫掠网格。由于在这个方向上的解是逐渐变化的，因此修改是合理的。与之前显示的自动生成的网格相比，该网格没有其他重大变化。

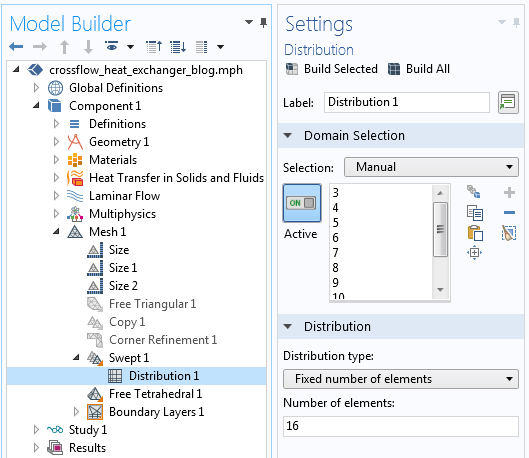
网格划分序列用于控制通道中沿流动方向的单元数量。

温度场分布和温度场之间的差异分布如下图所示。当然，使用扫掠网格的模型将有所不同。与之前的情况相比，这里某些区域的温度场相差约2°C。这种差异主要是由于跨界面的网格不同，而不是因为添加了额外的对连续性方程。在网格细化的极限下，两种方法都将收敛得到相同的解。使用装配体网格划分的主要优点是，我们可以从相对较粗糙的网格开始（该网格仍然会给出合理的结果），从而节省了初始模型开发的时间和计算资源。

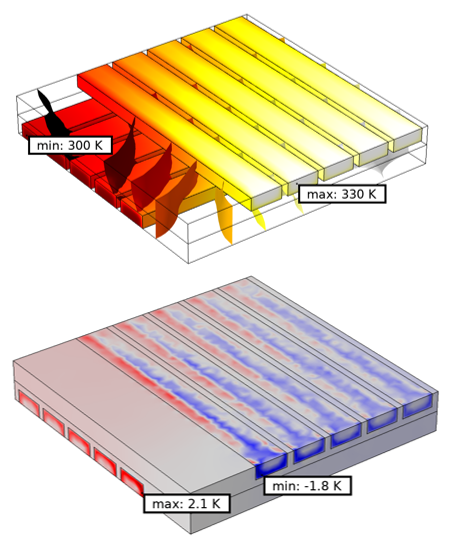
使用装配体网格划分的温度场（顶部），以及与默认网格的温度场差异（底部）。

对于这种几何结构，我们还可以以其他方式划分几何。我们可以沿流动通道之间的平面将模型分成两个对象，如下图所示。现在，我们可以进一步减少单元数量。尽管并非所有的几何形状都适用于此细分，但这种方法甚至可以进一步减少单元总数量。

另一种网格划分策略将在固体内，而不是在流-固边界处引入一致对。

结语

综上可知，装配网格划分是减少网格单元数量的有效技术。该技术特别适用于共轭传热问题，因为这些问题通常包含相对均匀的流动通道，便于扫掠网格。尽管这里我们介绍的是一个包括层流的模型，但是这种方法也适用于湍流问题。该技术在模型的初步开发中占有一席之地：我们通常需要对照具有一致网格的模型来验证这些模型，当然也需要进行网格细化研究。使用此技术的关键优势是我们可以更快地进行初步分析。

可在此处下载使用装配体网格划分功能的模型：

• 使用装配体网格划分模拟共轭传热