将全局方程引入全耦合目标搜索法

今天，我们将在 COMSOL Multiphysics^® 软件的模型中引入一个目标搜索方程，该方程与全耦合方法结合使用可以求解非线性问题。在计算上，尽管这种方法比我们之前介绍的分离式求解方法成本更高，但其在鲁棒性方面却具有一些独特的优势，并能够突显 COMSOL^® 软件的一个核心优势。

背景

正如之前的博客文章（在将目标搜索的方法引入分离式求解器）中所讨论的那样，我们可以使用一个额外的全局方程扩展多物理场模型，在该方程中，我们能够定义如何更新模型的输入来实现特定的输出。这种方法通过分离式求解的方法，依次解决问题（所有各种物理场问题）的一部分，然后通过全局方程来更新输入。

尽管这种方法在计算上非常有效，但是由于使用了分离式求解器，它依赖于临时更新方程，因此使用该方程需要对问题的底层物理知识有所了解。

这篇博文中，我们将介绍另一种替代方法。在该方法中，我们基于一个使软件计算符号导数的方程来更新输入。这种方法可能更加鲁棒和通用，但确实会带来计算成本。下面，我们先来看一下如何实现此方法，再说明其优缺点。

这里，我们仍以之前使用的同一示例模型来说明。即将两个电极施加到一个带有夹层的介质上的焦耳热问题。材料的电导率和热导率随温度呈非线性变化。我们模型的目标是调整顶部电极和接地电极之间的电势差，以使夹层的电流损耗为3瓦。

将全耦合求解器引入目标搜索

就像在我们之前的博客文章介绍的一样，这可以通过全局方程 来实现，尽管这一次，我们在物理场的影响范围内添加了一个额外的全局方程。但是，对于前一种方法，此额外方程在单独的分离式求解器迭代中使用临时缩放来更新施加的电势。在这篇文章介绍的方法中，当与受影响的物理场同时求解时，我们将使用一个对雅可比矩阵有贡献项的方程。

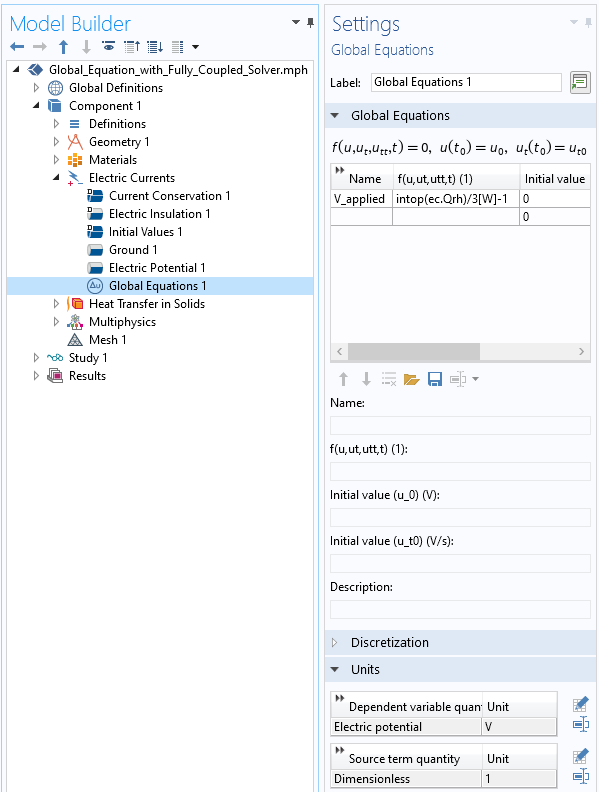
在物理场接口内引入全局方程。

下面，我们修改之前的示例并进行演示。我们仍然需要为施加的电势引入一个全局方程 V_applied，但是现在我们需要一个满足电势方程且同时求解的方程。为此，我们在电流 物理场中添加了 全局方程 特征。注意，我们输入的残差方程在解点必须等于零。我们输入的方程是：

intop（ec.Qrh）/ 3 [W] – 1

其中，intop() 是一个在夹层中定义的积分算子。稍后我们将看到该方程的无量纲化的一些优势。方程重新排列后等效于：

intop（ec.Qrh）= 3 [W]

这可以理解为：计算 V_applied 的值以使夹层中的损耗等于 3 瓦。我们还可以写出该残差方程表示的内容：

在计算雅可比贡献时，对于模型中的所有未知数，我们采用其符号导数。通过检查，我们可以看到：

而关于电势的其他两个导数 \partial r / \partial V，以及温度场 \partial r / \partial T，将为非零。这意味着全局方程在 Jacobian 对角线处引入零，但在相应行中引入了许多非零项。这影响了我们必须在非线性迭代中使用的线性系统求解器的类型。

这些附加项才是真正有趣和有用的贡献。这些项告诉非线性求解器如何更新 V_applied，以使我们的全局方程等于零。也就是说，软件会自动找出 V_applied（全局方程）要更新的内容。（回想一下以前的方法，我们必须根据一些物理知识来构建自己的更新方程。）

引入非零梯度

但是，这些附加项会产生计算成本。它们确实要求我们同时求解全局方程和电势方程，并且由于它们同时引入了非对角项和对角线为零，因此它们要求全耦合方法在求解电势场和全局方程时，使用直接线性求解器。此外，以上所示的导数在初始条件下必须为非零，否则雅可比行的整个行将为零。在这种情况下，这有点不太容易实现，因为在指定的初始值处电势必须存在非零梯度。

有两种方法可以在电势中引入非零梯度。最简单的方法是在电流物理场中指定一个空间变化的初始条件，如下面的屏幕快照所示。这很容易做到，至少在这种情况下，但是可能并不总是有效，因为我们确实引入了非物理的初始值。

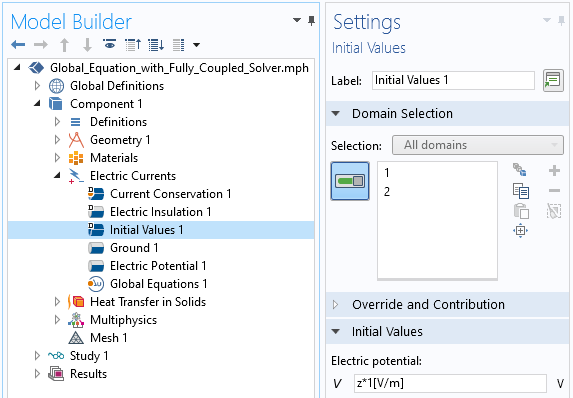
将初始值引入电流物理场将导致电势场的非零梯度。

一个更好的方法是引入一个全局方程 变量 V_applied 来求解方程：

V_applied / 1 [V] – 1

该方程简单地设置 V_applied 等于 1[V]，然后软件将求解方程组并计算一致的电势场。请注意，这就是为什么使用无量纲的残差方程会有所帮助的原因。如下面的屏幕快照所示。

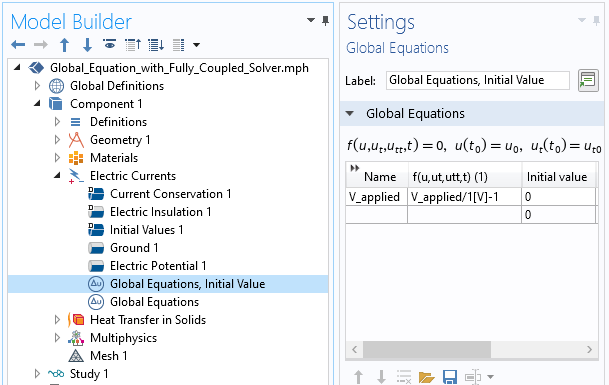
引入一个额外的全局方程以查找初始值。

调整全局方程的求解器设置

一旦我们求解了这个固定值 V_applied，并切换回使用原始的全局方程，就可以将该问题的解用作初始值。在 COMSOL 软件中，这可以通过修改研究步骤的模型配置 复选框，然后在两个研究步骤 中启用/禁用两个不同的全局方程来实现。也就是说，在第一个研究步骤中，我们只需指定 V_applied，然后在第二个步骤中求解 V_applied，以使夹层中存在所需的损耗，如下面的屏幕快照所示。

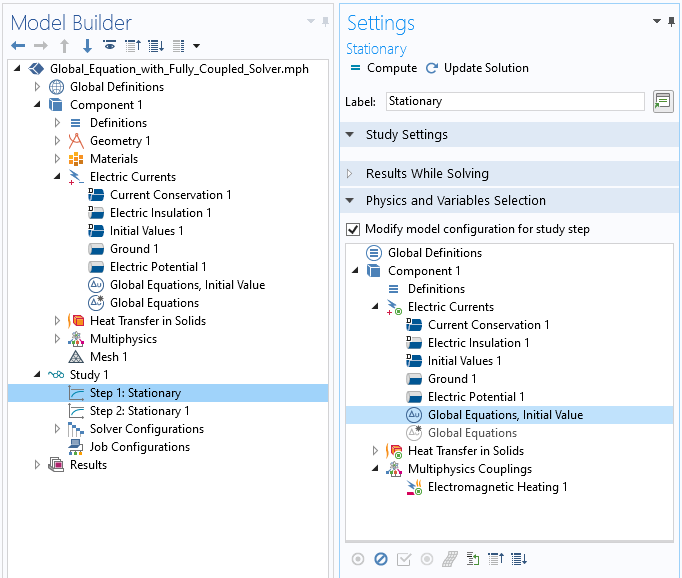
修改第一步研究的模型配置，其中求解初始值的全局方程。在第二步中，应用相反的设置。

第二步确实需要调整默认求解器设置。我们有两种选择：

1. 对整个问题使用全耦合的方法，并使用直接求解器。这对求解器设置的更改要求最少，但是使用直接求解器求解大型方程组将需要大量内存。
2. 使用分离式求解器，但将全局方程和电势方程合并为一个步骤，使用自动牛顿法和直接求解器将其求解为收敛。仍然可以使用迭代求解器以分离的方式求解温度解。此方法需要对设置进行更多更改，但需要的内存较少。请注意，这种分离会导致项被忽略（如果它们根本存在），有时可能会对收敛产生负面影响。这些设置的更改如下面的屏幕快照所示。

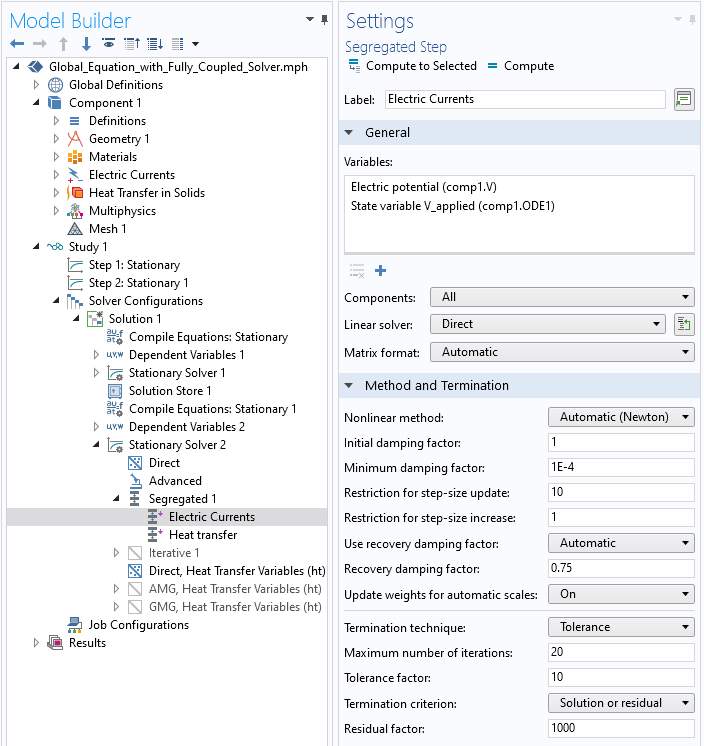
全局方程和电势必须同时使用直接求解器求解。

建议从第一种方法开始，如果内存要求太高，则尝试第二种方法。请注意，对于三维模型，直接求解器的内存需求随着问题的大小而迅速增加，这是主要的限制。

结束语

今天我们介绍的是一种可用于解决 GUI 中搜索目标问题而无需依靠任何编程的方法。在之前的文章中我们还讨论了解决此类问题的其他方法：

1. 使用优化模块
2. 使用参数化扫描并手动识别近似目标值
3. 用附加的更新方程增强分离的求解器

尽管需要更高的内存，但今天介绍的全耦合目标搜索法的显著优点是它可以快速而稳定地收敛。注意，该技术也可以在时域中使用，只要可以在每个时间步上满足全局方程即可。

这种强大而快速的收敛是雅可比矩阵内附加项的结果，并突显了 COMSOL Multiphysics 在解决高度非线性耦合的多物理场问题上的另一项技术优势。这项技术以及前面讨论的技术，对于分析师而言，都是一种很有用的工具。

自己尝试