用间断伽辽金法模拟线性超声波

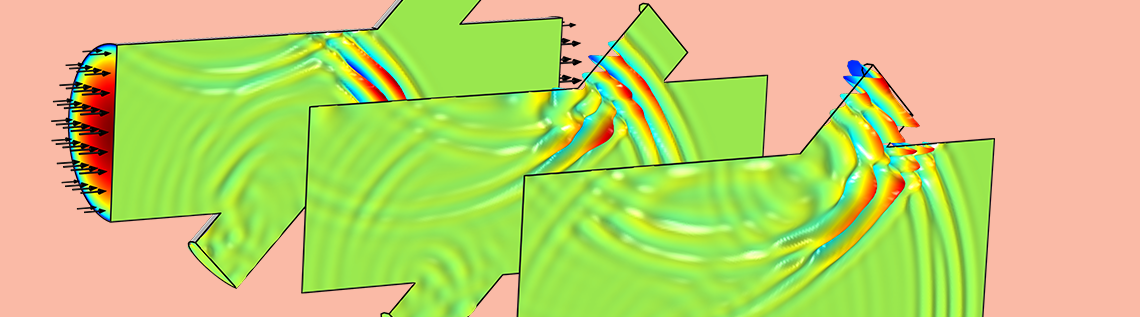
对声学上的大计算量问题进行建模，需要使用间断伽辽金法（discontinuous Galerkin method）这样节约内存的方法。为了更容易地解决这类问题，COMSOL 软件的声学模块中添加了一个基于这种方法的物理场接口 对流波动方程，时域显式 接口。它可以包含稳态背景流，并且适合于线性超声波问题的建模。今天，我们将以超声波流量计为例，探讨如何使用该接口。

对流波动方程，时域显式 物理场接口

对流波动方程，时域显式 接口建立在声学模块的功能上。这个接口所使用的是间断伽辽金(DG)方法，也称为 DG-FEM，它依赖于时域显式并非常节省内存的求解器。对流波动方程，时域显式 接口能够有效地求解稳态背景流中包含许多波长的大型瞬态线性声学问题。它还包括吸收层(海绵层)，可以作为有效的非反射边界条件。

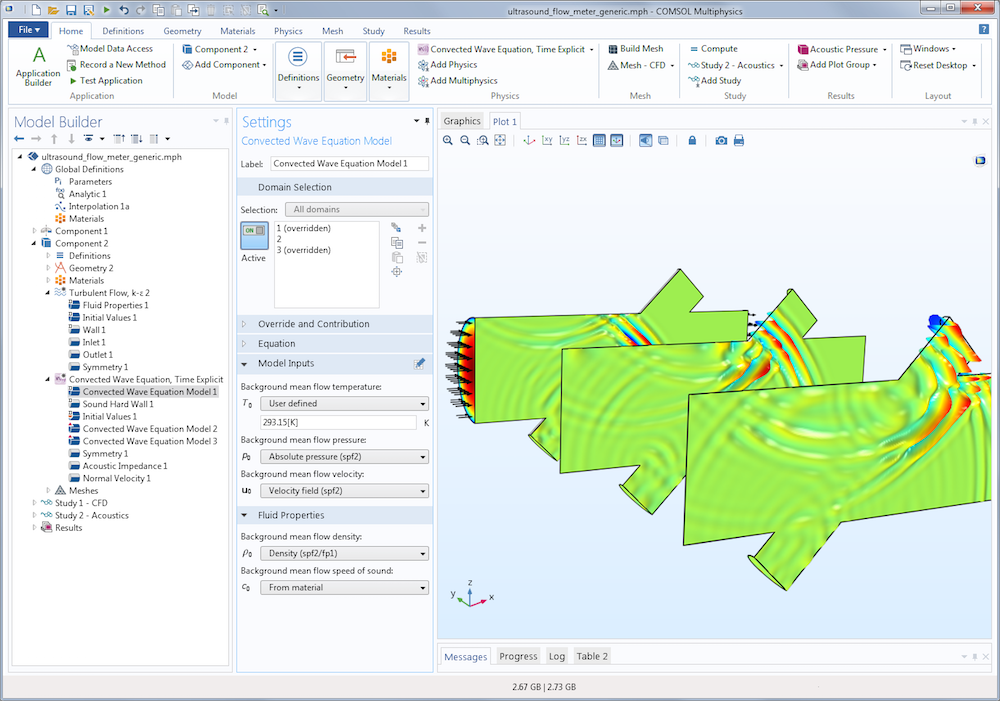
使用 对流波动方程，时域显式 接口建立的超声波流量计模型。同时包含湍流模型，用于计算通过流量计的背景流量。

使用吸收层截断计算域和节省内存的 DG-FEM 公式，我们可以在时域中设置和求解大计算量的问题，这些问题是根据可以求解的波长数量来测量的。因此，对流波动方程，时域显式 接口适用于模拟相对于波长而言距离较远的声信号传播。

该接口适用于线性超声问题，例如考虑飞行时间参数的超声流量计和超声传感器。同时也适用于非超声问题，例如室内声学和汽车驾驶室内音频脉冲瞬态传播。

求解线性欧拉方程

由对流波动方程，时域显式 接口求解的控制方程是线性欧拉方程。这些方程假设一个绝热状态方程(见参考文献1和参考文献2)。质量和动量守恒方程如下:

 
其中，声压 p 和声速扰动 u 是因变量。声速 c₀ 以及稳态平均背景流变量通过密度 ρ₀，压力 p₀ 和速度场 u₀ 使用下标 0 定义。

背景流可以是速度梯度范围从小到中等的稳定流。当背景速度设置为零时，方程被有效地简化为对经典波动方程进行建模。请注意，在接口中没有物理损耗机制，并且上述方程被设置为守恒形式。

用时域显式方法提高效率

如上所述，对流波动方程，时域显式 接口是基于 DG 方法建立的，该方法是一个节省内存的时域显式公式。通过这种方法，当时间向前步进时，不需要对整个系统矩阵求逆。相比之下，时域隐式方法需要对这个矩阵求逆，而这在求解大型问题时会消耗大量内存。在 DG-FEM 法中，在时间演化之前，，只对一个参考网格单元进行少数质量矩阵求逆(使它们的尺寸变小)。该方法也是无需求积的。对于 DG 方法，计算局部通量矢量和通量散度是一个耗时的过程，我们可以通过基础线性代数子程序库（Basic Linear Algebra Subprograms，BLAS）三级运算，即矩阵间运算高效地运行。

隐式方法有时被认为能更快地求解匹配内存的中小型问题。然而，这并不总是正确的。我们在对两种方法进行比较时，查看误差量级很重要。使用隐式方法时，很容易使用太大的时间步，这会从时间方法上引入误差。另一方面，由于单元的不连续，对于相同的多项式阶数和网格，DG 方法更精确。

基于有限元方法的物理接口，例如 压力声学，瞬态 或者线性纳维–斯托克斯，瞬态 接口需要使用时域隐式方法。挑战在于，当增加模型大小或频率时，隐式方法的内存消耗会快速增长。增加频率导致内存快速增长是由于系统中的最小波长必须用一定数量的网格单元来解析。尽管如此，有限元方法更加灵活，可以很容易地耦合进多物理场问题中。

对流波动方程，时域显式 接口在其默认的公式中使用四次(四阶)形状函数，这是用 DG 方法求解波动问题时速度和效率的最佳选择。这允许我们可以使用大约是波长一半的网格单元大小来求解需要解析的最高频率分量。这样反而简化了大型问题的网格划分。

例如，下面给出的超声波流量计模型由760万个自由度组成，可以在台式计算机上求解，使用 9.5GB 内存。用一个隐式公式在台式机上求解这么大的模型是不可思议的。由于代码是完全并行运行的，因此求解时间不太取决于可用的内存，而更多地取决于处理器速度和可用的内核数量。DG-FEM 公式非常适合并行化。

在声学模块中，COMSOL 计划在未来更多地使用 DG-FEM 公式，因为我们相信它对于求解大型波动问题确实有效。我们还在不断地改进和微调方法和求解器。

吸收层特征

如上所述，对流波动方程，时域显式 接口含一个吸收层 特征。这是一种海绵层，类似于已经存在于许多频域接口中的完美匹配层(PML)。不同之处在于吸收层结合了坐标缩放、滤波和低反射阻抗条件。

在吸收层的域内，坐标缩放有效地降低了波传播的速度，并确保它们与向外部边界“对齐”(垂直)。这意味着波以更接近法线的方向撞击外部边界。滤波功能衰减并滤除缩放产生的波的高频分量。在该层的外边界，由于确保了垂直入射，简单的平面波阻抗条件消除了所有剩余的波。下面的动画使用均匀流中的高斯脉冲2D模型:对流波动方程和吸收层基准教程，演示了吸收层的作用。

均匀背景流中高斯脉冲的时间演化。气流以 0.5 马赫的速度向右侧移动。吸收层吸收出射波。

在 COMSOL Multiphysics® 中模拟线性超声波问题

作为对流波动方程，时域显式 接口的应用示例，我们来看一个通用的湿式飞行时间配置的超声波流量计设置。湿式超声波流量计中有用于超声波信号的专用信号管，整个装置安装在测量流量的管道中。为了估计主流动的速度，计算同时穿过上游和下游的两个信号的到达时间差。

在这个模型中，流量计中充满水，主流管的直径为 5mm。下图显示了使用对称条件的背景流场。主通道中的平均速度为 10m/s (请注意，需要使用CFD模块模拟流动。)。信号管是与主通道成 45° 角的小型侧导管。

要了解有关此模型的更多信息，请访问 COMSOL 案例库。

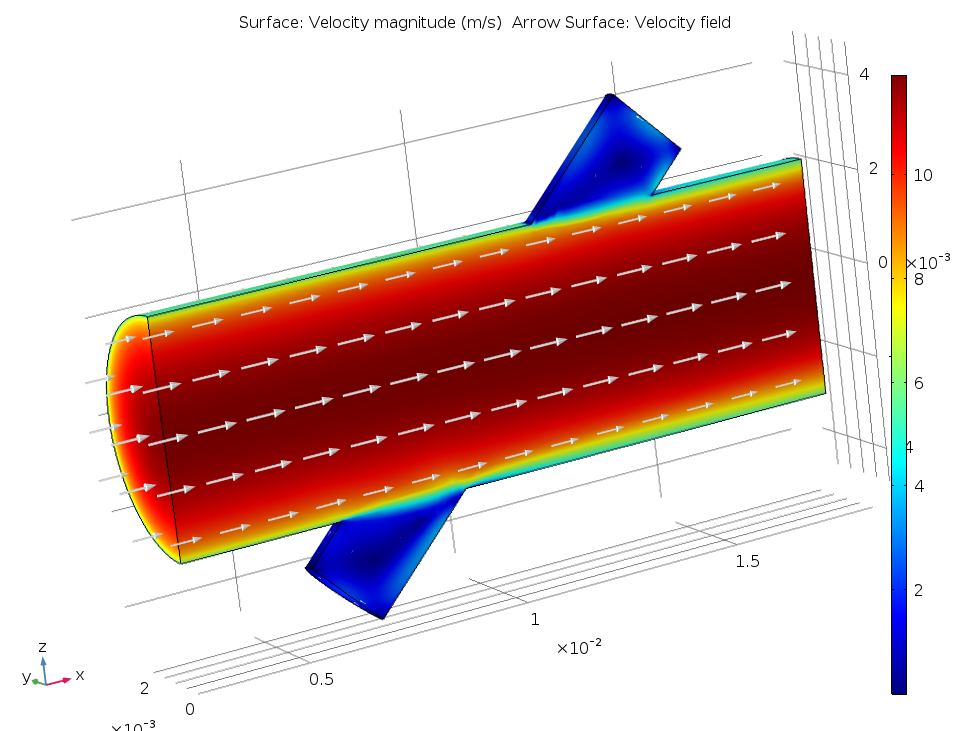
超声波流量计内的背景平均流量。

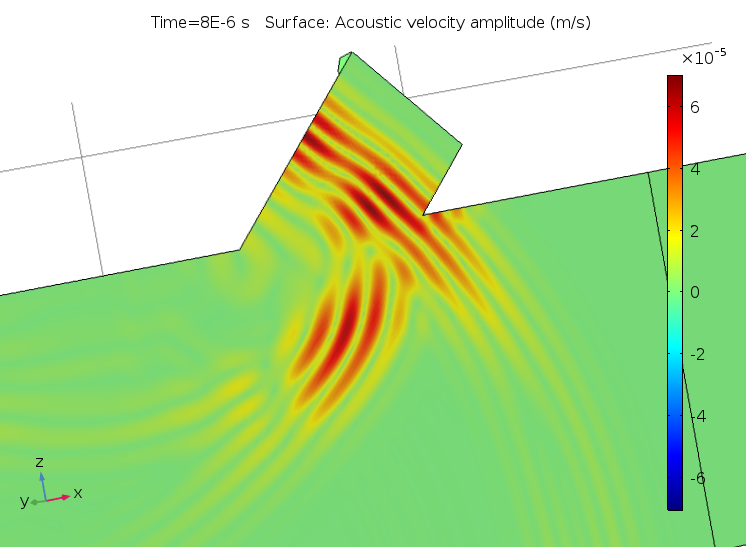
下面的动画显示了声脉冲在信号管下游的传播，与背景流的相互作用，以及衍射效应。该信号是具有高斯脉冲包络的 2.5MHz 谐波载波。在主管道的入口和出口处有吸收层。动画中仅显示系统对称平面上的压力信号幅度。如前所述，此声学模型求解 760 万自由度，可以在台式机上运行，使用 9.5GB 内存。

声脉冲通过超声波流量计中的信号管向下游传播。

下图显示了上行(绿色)和下行(蓝色)脉冲传播的接收信号。我们测量两个信号之间的到达时间差为 49ns，并使用它来估计平均流速，得到 10.75m/s 的值。虽然实际值为 10m/s，但我们知道结果的差异是由于流动剖面校正因子(FPCF)引起的，这是该模型的一个重要参数。通过模拟，我们可以计算出 FPCF 值，因为流场是通过仿真获得的已知先验项 。我们还可以优化流量计的几何形状，并测试不同的检测信号。

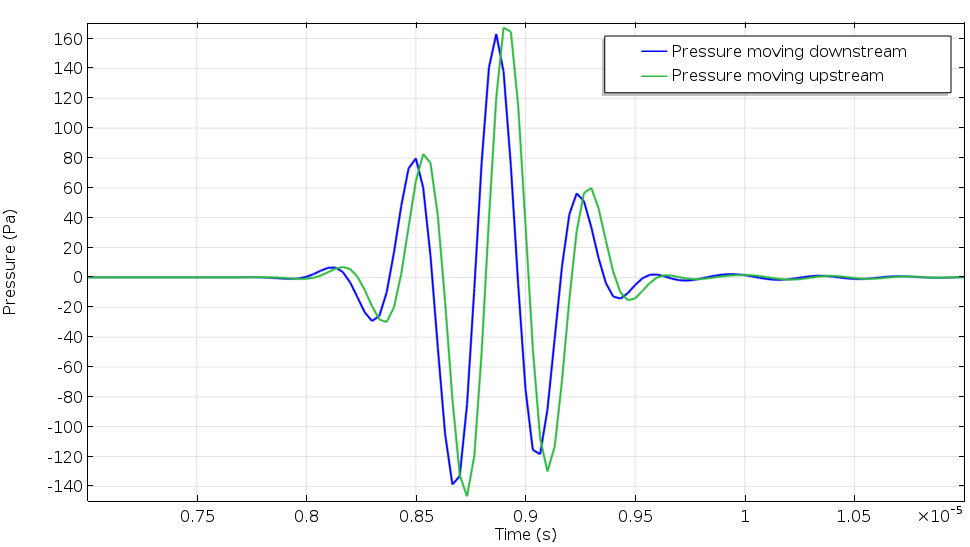
超声波流量计中向上游和下游移动的信号所产生的压力信号曲线。到达时间差用于预测超声波流量计中的平均流速。

对流波动方程，时域显式 接口的常规建模考虑事项

编者注: 从 COMSOL Multiphysics 5.3 版本开始，一个新的网格质量优化程序可以用来加速 DG 方法。这种优化对此方法的性能极为重要，在需要时尽可能使用。要了解更多信息，请访问 COMSOL 发布亮点页面或参见声学模块用户指南。

当使用基于 DG-FEM 公式的 对流波动方程，时域显式 接口时，有一些常规的建模考虑值得了解。有些实践应用与声学模块中基于有限元的接口不同。这些指导建议也可以在声学模块用户指南 中的“用对流波动方程接口建模”部分找到。

设置吸收层

就像 PML 一样，吸收层由模型树中的定义 节点中设置，通过将吸收层添加到表示该层的几何实体中。(如同 PML，在创建几何时建议使用层 选项。)一旦建立好吸收层，我们需要在该层的最外层边界上放置声阻抗边界条件。虽然缺省值通常能满足仿真需求，但对于高级用户来说可以启用高级物理选项，修改吸收层的过滤器参数。

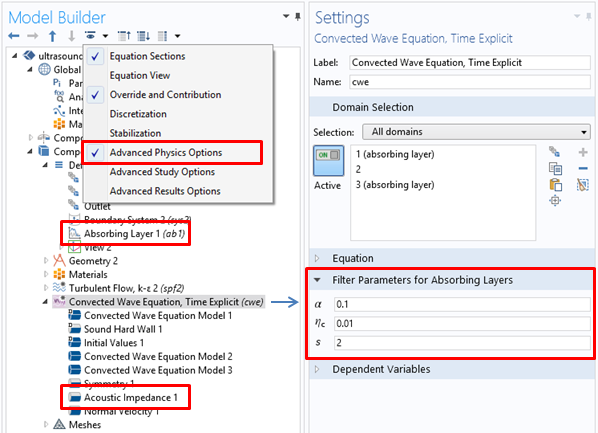
吸收层特征和声阻抗边界条件的设置。

剖分网格

使用对流波动方程，时域显式 接口的模型划分模型网格与声学模块中的大多数其他物理接口略有不同。因为默认设置是使用四阶形状函数，所以我们通常可以通过网格单元大小设置为 λ_min/2 和 λ_max/1.5 之间的任意值来获得适当的空间分辨率。请注意，时域显式方法的内部时间步进大小由 CFL 条件严格控制，因此网格大小也是如此。这意味着模型中最小的网格单元控制时间步长，因此尽可能避免小的网格单元是一个好主意。用于对流波动方程，时域显式 接口的内部时间步长是 COMSOL Multiphysics 软件根据网格和物理特性自动选择的。

存储数据以减小模型尺寸

当求解包含数百万自由度的大型瞬态模型时，输出中的数据量可能非常大，并会产生存储许多千兆字节的文件。只存储后处理所需的几何实体上的数据是减小模型尺寸的好策略；例如，在对称平面上、沿线或点上。我们可以在 COMSOL Multiphysics 中通过使用 在输出中存储物理场 功能(位于因变量值 部分)。在这里，我们可以决定必须存储哪些选择数据。请注意，在研究设置 中指定的时间 是存储解的时间，与内部时间步进无关。

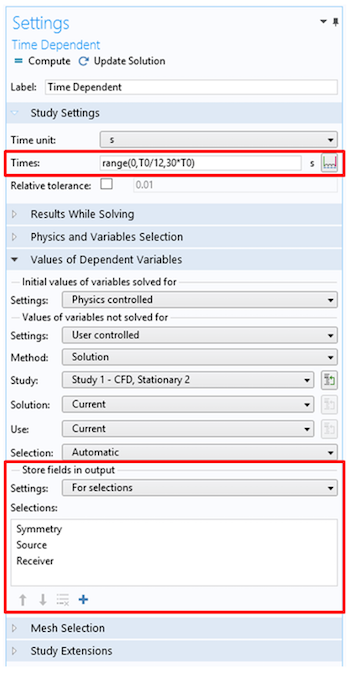
减少存储文件的大小可以通过设置解的存储时间来实现，并且只将数据保存在您需要的选择中。

对结果进行后处理

当分析使用对流波动方程，时域显式 接口模拟运行的结果时，我们需要记住是使用四阶单元离散了因变量。这意味着在网格单元中，形状函数具有很大的自由度，并且可以包含很多空间细节。我们可以通过为绘图的质量部分设置高分辨率。求解模型时，生成的默认图已经选择了此选项，并设置为自定义分辨率并将单元细化 设置为6。当添加更多用户定义的绘图时，我们必须更改分辨率。

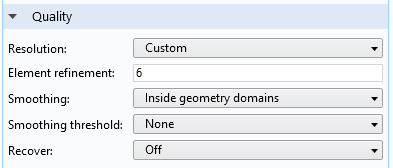
属性设置自定义分辨率单元细化设置为 6 可确保解呈现良好的空间分布。

下图显示了默认绘图的自定义分辨率设置和添加用户定义绘图的默认分辨率之间的差异示例。乍一看，左边的解好像不正确。但是，一旦在质量部分选择了正确的分辨率，它便能显示解的真实波动性。

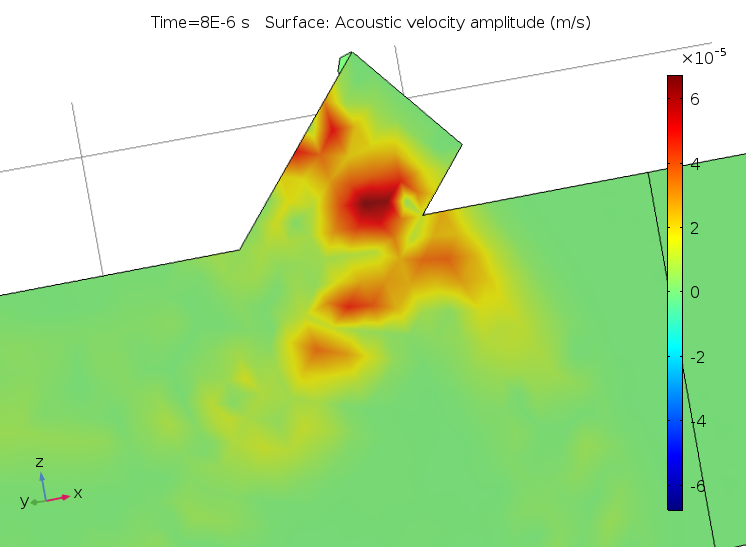
分辨率不正确的声速图(左)和正确配置的高分辨率声速图(右)。

编者注:此处显示的性能数值已经随着 COMSOL 5.3 的发布更新。我们将继续致力于在软件的未来版本中提高这些数值。

了解更多在 COMSOL Multiphysics® 中的声学建模应用信息

• 下载这篇博文中使用的模型:
  • 通用传播时间法超声波流量计
  • 均匀流中的高斯脉冲二维模型:对流波动方程和吸收层
• 了解 COMSOL 博客中的其他声学建模应用
• 进入发布亮点页面，查看声学模块的其他更新

参考文献

1. A. D. Pierce, “Acoustics, An Introduction to its Physical Principles and Applications,” Acoustical Society of America (1991).
2. A. D. Pierce, “Wave equation for sound in fluids with unsteady inhomogeneous flow,” The Journal of the Acoustical Society of America. 87, pp. 2292 (1990).