译者注:本篇博文介绍了什么是“网球拍效应”,它是如何命名的以及为什么会发生这种现象。使用 COMSOL Multiphysics 的多体动力学模块,我们可以模拟该效应,并通过仿真 App 深入理解该效应背后的数学原理。
发现 Dzhanibekov 效应
20 世纪 80 年代,人类对太空的探索活动进行得如火如荼。1985 年,苏联太空站 Salyut 7(礼炮 7 号)在绕地球飞行时出了一点问题,所有系统都已经关闭,俄罗斯科学家与 Salyut 7 失去联系,飞船开始偏离轨道运行……
宇航员 Vladimir Dzhanibekov 和 Viktor Savinykh 被派去拯救飞船。这是一个艰巨的任务。据屡获殊荣的历史学家和科学作家 David SF Portree 称,这是“历史上最令人印象深刻的太空维修壮举之一” 。
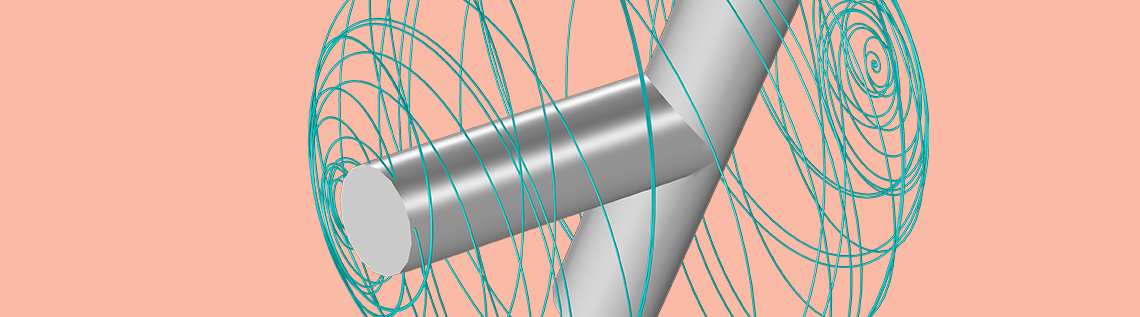
在维修过程中,来自地球的补给被带有三个旋转轴的蝶形螺母锁定。当 Dzhanibekov 拧开螺母时,他注意到一种奇怪的行为:蝶形螺母先发生旋转,然后翻转。如下面的动画所示,我们用一个简单的T形物体演示了与螺母相同的运动行为。
Vladimir Dzhanibekov 注意到太空中的螺母的独特效应,这里我们使用简化的几何图形来演示。
这种效应并不是魔术,而是一种数学现象。
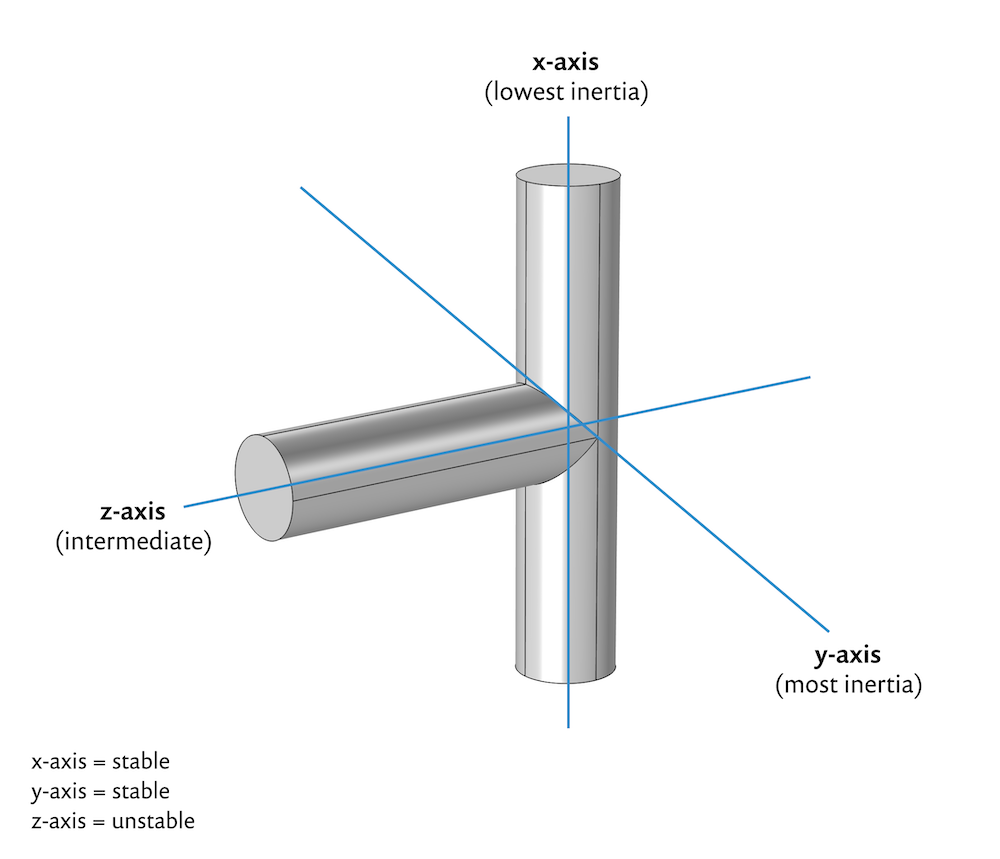
对于一个三维物体,可以识别出三个特殊的旋转轴。这些轴具有以下特性:当物体以一定的角速度围绕其中一个轴旋转时,物体的角动量等于角速度和对应于该旋转轴的惯性矩的乘积。这类惯性矩称为惯性矩,并且旋转轴称为旋转主轴。
对于某些物体,旋转主轴很容易识别,例如上面简化的螺母形状、谷物盒和手机等常见物体。
螺母与网球拍有什么关系呢?
上述 Dzhanibekov 效应也被称为中间轴定理 或网球拍定理。网球拍也具有三个易于识别的旋转主轴,因此它们表现出与蝶形螺母相同的行为。
在 1980 年代,Dzhanibekov 注意到这一现象之后,将其保密了多年。然而,一个数学家团队独立发现了网球拍中的运动效应,并阐明了其背后的数学原理。六年后,他们发表了论文《扭曲的网球拍》。
该效应的复杂发现历史就是为什么用Dzhanibekov 效应和网球拍定理命名中间轴定理的原因。现在,我们已经知道网球拍效应的名字以及它的来源,那么,这种现象是如何起作用的呢?
欧拉运动定律
刚体的旋转由欧拉运动定律描述。欧拉运动定律是牛顿定律的扩展,即将牛顿的点粒子扩展到刚体(例如手机或谷物盒)。欧拉方程如下所示:
这里,I_i 是三个主惯性矩,\omega_i 是角速度沿主轴的分量,M_i 是扭矩。
惯性矩的值表示围绕该轴产生单位角加速度需要多少扭矩(换句话说,使其旋转得更快或更慢)。最高的惯性矩需要最大的转矩,而最低的惯性矩则需要最小的转矩。
对于刚体绕 3 个轴自由旋转的情况,我们可以判断该旋转在什么条件下稳定或不稳定。这是通过假设绕 1 轴和 2 轴的角速度有微小扰动来实现的。通过对欧拉方程的一些处理,我们得出以下方程:
\omega^2_3\right]\omega_1 \,\,\, \,\,\, I_1 \neq I_2 \neq I_3
方括号中的部分只是一个常量(我们称之为 k)。该常数取决于主惯性矩的值,可以为正或为负。如果 I_3 大于 I_1 和 I_2(即 I_3 是最大的惯性矩),那么(I_3 – I_2)和(I_3 – I_1)都是正值,因此 k 是正值。同样,如果 I_3 小于 I_1 和 I_2(即 I_3 是最小的惯性矩),那么(I_3 – I_2)和(I_3 – I_1)都是负数,也是正值。
可以得到
这个式子看起来是不是很熟悉?这是简单谐波运动的方程式-k<0。因为,因此这是一个稳定的运动,意味着微小的扰动不会使物体脱离平衡。
如果 I_3 不是最大或最小的惯性矩,会怎样呢?例如,假设 I_3 大于 I_2,但小于 I_1。那么,k 变成负数。加上括号外的负号,则整体上我们得到一个正的常 数,因为 -k>0。这个方程是不稳定的。
换句话说,此时物体的稳定性就如在刀刃上行走:无论多小,任何力都会使它跌落。
通过多体分析演示物体的中间轴定理
现在,我们不需要去太空就能观察到这种现象。我们可以使用 COMSOL Multiphysics® 软件进行多体分析,探索 Dzhanibekov 效应。
以一个铝制 T 形杆为例,它由两个铝柱组成,其半径为 1 厘米,Z-轴的高度为 7 厘米,X- 轴高度为 10 厘米的,如下图所示。

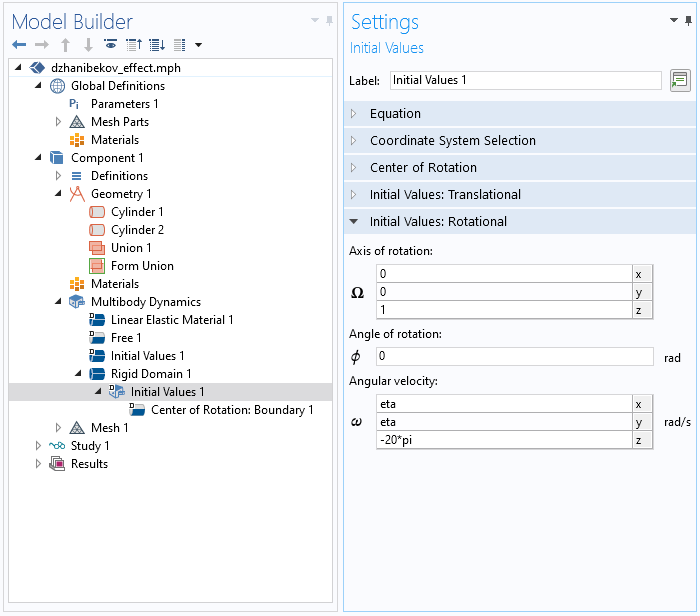
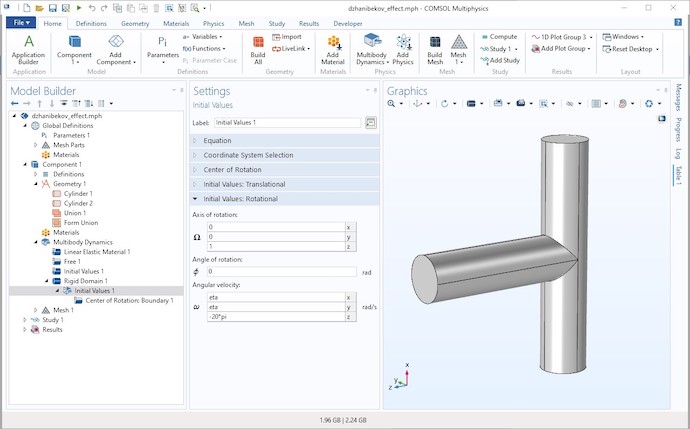
使用 COMSOL Multiphysics 的附加模块——多体动力学模块,我们可以添加刚性域 边界条件并选择域以使其成为刚体,选择密度为来自材料 。
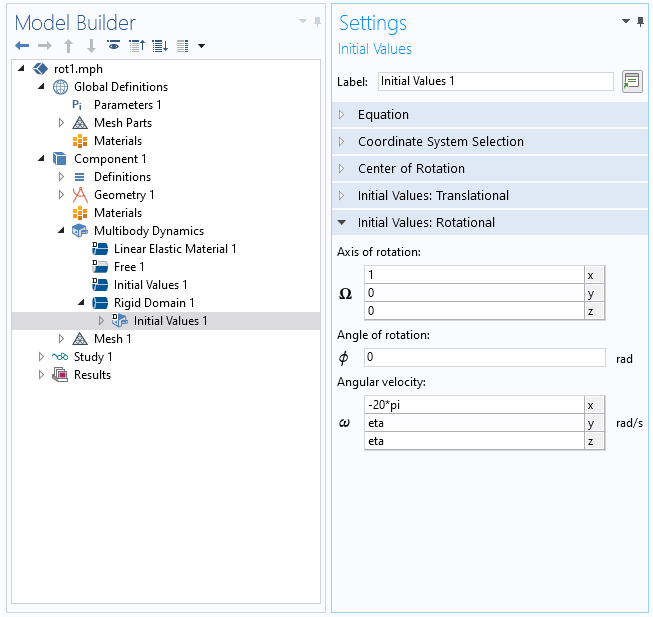
我们可以将模型设置为在 z 轴上旋转,旋转轴和角速度的值显示如下:
仿真演示了 T 形杆的末端如何移动,以便我们可以分析其随时间变化的位置或位移。
我们可以更改或添加不同的参数值,以查看它们如何影响 T 型杆的稳定性,例如更改旋转轴和角速度。
| x-axis | y-axis | z-axis |
|---|---|---|
|
|
|
|
在X-,Y-和Z-轴上旋转时的T形杆。
通过在 T 形手柄的末端添加一个点,我们可以更轻松地可视化该效应。也使我们可以通过使用表达式sqrt(u2+ v2)绘制位移大小来可视化 T 形手柄相对于旋转主轴的位移。在下图中,当T形手柄的末端与 z 轴正好对齐时,位移量为零,并保持稳定,直到开始翻转。这张图更清楚地表明,翻转之间存在稳定区域。
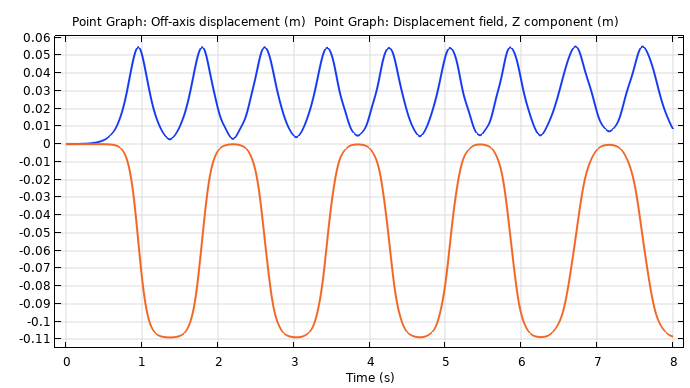
蓝线显示离轴位移(稳定),橙色线显示 Z 分量的位移场(不稳定)。
为了更形象地演示此概念(和一维绘图),下面的动画显示了 T 形手柄绕 z 轴在轨道中移动时的位移,我们可以使用点轨迹 图来显示。我们会看到,当模型变得不稳定时,轨道会变大,并在该点到达另一端时很快稳定下来(该过程会不断重复)。
使用仿真 App 演示 Dzhanibekov 效应
COMSOL Multiphysics 包含模型开发器,我们可以使用它将数值模型转换为具有专用输入和输出的直观用户界面。作为示例,我们构建了一个上述 T 型杆模型的仿真 App。
1Dzhanibekov效应仿真App的屏幕录像。
我们可以使用此仿真 App 进行测试:
- 3 种不同的几何形状
- 原始的 T 形杆几何
- 网球拍
- 手机
- 旋转轴
- X
- Y
- Z
注意:手机和网球拍的几何形状在 x 轴上不稳定,而T形杆在 z 轴上不稳定。
我们也可以使用该仿真 App 播放选定几何图形和轴的动画。
如果您想在现实生活中证明这种效应,COMSOL 对您的手机或网球拍的任何损坏可不负责。实际上,使用该仿真 App 可能是更安全的选择!
案例模型
下载仿真 App 演示案例模型,选择一种几何形状,选择旋转轴,然后看看会发生什么:




评论 (0)