
为了保证岩土工程建设的安全性,在施工时要求具有特定地基和结构加固。实地测试的成本极高,因此仿真就显得非常实用,甚至必不可少。人们开发了很多数值模型来深入研究土壤行为。在这里,我们将向您介绍 COMSOL Multiphysics 中用于研究土壤的运用最为普遍的模型,及对隧道开挖实例进行分析。
岩土工程快速入门
建筑界普遍存在这样一个趋势:海上结构物建造的水域越来越深;建筑物之间的距离越来越近;海上风力发电机建造在离海岸很远的深海中,这使其可能面临着极其严苛的负载条件。因此,近几十年来,岩土工程师开发了多种数值仿真来应对这种建筑趋势以确保建筑的安全性。

“Paris Metro construction 03300288-3″。已获 Public domain 许可,通过 Wikimedia Commons 共享。
塑性与岩土材料
塑性是指材料能稳定地发生永久变形而不破坏其完整性的能力,金属、土壤、岩石、混凝土等材料便具有这样的特性。当造成弹性形变的应力上升到达一个特定的应力级别——屈服应力时,材料开始产生塑性形变。
弹/塑性行为是与路径相关的,应力取决于材料的之前的变形行为。因此,塑性模型通常与应力变化速率直接关联,而非应力和塑性应变。整个行业中应用最为广泛、最著名的塑性模型是以 von Mises 屈服面为基础的,该模型中塑性流动不因压力的大小而改变。因此,屈服条件及塑性流动只以偏应力张量为基础。
然而,因为分析土壤物质时需考虑摩擦和膨胀的影响,所以该模型对此类材料无效。让我们来看看该如何解决这个问题,并简单介绍一下 COMSOL Multiphysics® 仿真软件中不同的土壤塑性模型。
土壤及岩石的塑性
对于土壤和岩石等材料,摩擦和膨胀的影响是不可忽略的。众所周知,这类材料对压力非常敏感,当施加压力时会产生不同的拉伸和压缩行为。因此,上文所述的 von Mises 模型不适用于这类材料,人们转而通过求解屈服函数来研究摩擦材料的行为。
让我们通过如下图所示的滑块来阐释这类材料的摩擦行为和塑性流动。
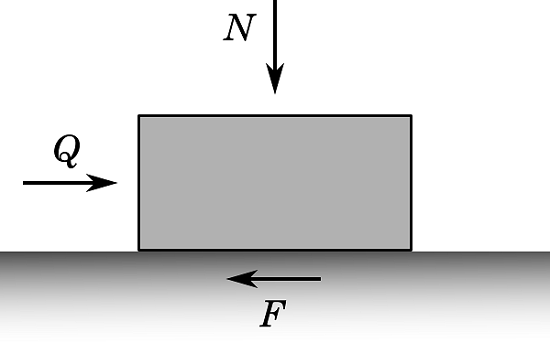
如图,向滑块施加一个垂直载荷 N 及一个切向载荷 Q。假设滑块被放置在一个带有静摩擦系数为 \mu 的表面上,根据库仑定律,滑块在滑动前可以承受的最大力为 F=\mu N 。因此,当满足以下条件时,滑块开始滑动:
(1)
滑动方向为水平方向。对于切向载荷来说,当 f<0 时,滑块不会滑动;当 f=0 时,滑块将会向外加载荷 Q 的方向滑动。第一个土壤塑性模型是在 Mohr-Coulomb 准则的基础上开发的,它是对获得连续材料和多轴应力状态方法的一种概括。它被定义为:当任何平面内的剪应力与平均正应力的组合达到临界条件时,材料开始屈服甚至断裂。该临界条件如下所示:
(2)
在这里,\tau 是剪应力,\sigma 是垂直应力,c 是内聚力,代表垂直应力为 0 时的抗剪强度,\mu=\tan\phi 是出自著名的库仑摩擦模型的内摩擦系数。该方程代表 Mohr 平面内的两条直线。当三个 Mohr 圆都位于这两条直线之间时,应力状态为安全;而当这三个圆中的一个与这两条直线相切时,即为临界状态(材料开始屈服)。
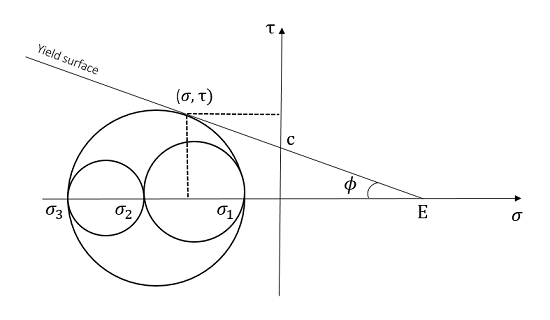
Mohr-Coulomb 屈服行为。Mohr 圆以主应力 \sigma_1 、\sigma_2 及 \sigma_3 为基础。正如你看到的,当其中一个圆与屈服面相切时,材料便会发生屈服。
如上图所示,应力状态按照 \tau=\frac{1}{2}(\sigma_1-\sigma_3)\cos\phi 及 \sigma=\frac{1}{2}(\sigma_1+\sigma_3)+\frac{1}{2}(\sigma_1-\sigma_3)\sin \phi 这两个公式进行计算。因此,屈服准则及方程 2 可以被广义表达为以下形式:
(3)
它甚至可以被看作是以库仑摩擦为基础的更通用系列准则的一个特例,可以表达为以应力张量的不变量为基础的方程式:
(4)
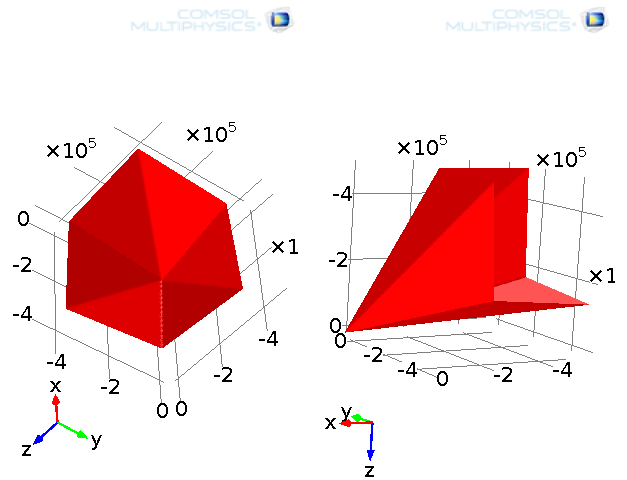
Mohr-Coulomb 屈服函数表示法。
Mohr-Coulomb 准则对主应力空间内的六棱锥进行了定义,这为直接对该准则进行分析提供了很大的便利。但是,由于尖角(例如屈服面的法线在尖角处是未被定义的)的存在,很难对本构方程从数值计算的角度进行处理。
为了避免与尖角有关的问题, 另一个屈服准则——Drucker-Prager 屈服准则被开发了出来,它是通过对 von Mises 屈服准则进行修改而得到的,这一准则不仅将库仑摩擦纳入考虑范畴,还建立了与流体静压的依赖关系:
(5)
这个方程表示主应力平面内的平滑圆锥,而不是六棱锥。如果系数 \alpha 和 k 与Mohr-Coulomb 准则中的系数互相匹配,即如下所示:
(6)
Drucker-Prager 屈服面会穿过 Mohr-Coulomb 六棱锥的内部或外部顶点,这取决于符号 \pm 为正还是为负。塑性流动方向来源于所谓的“塑性势”,它既可以是与塑性势的方向相同的,即与塑性相关;也可以不同,即与塑性无关,发生屈服现象(屈服函数)。我们可以据此开发很多不同的非关联流动法则。
在 Drucker-Prager 模型中,可以利用关联法则使体积塑性流动不为零。因此,在施加压力的情况下体积会发生变化。然而,这与许多土壤材料,特别是颗粒材料的行为是相矛盾的。相反,可以在塑性行为是等体积的(体积守恒)情况中使用非关联流动法则,这能更好地反映颗粒材料的塑性行为。
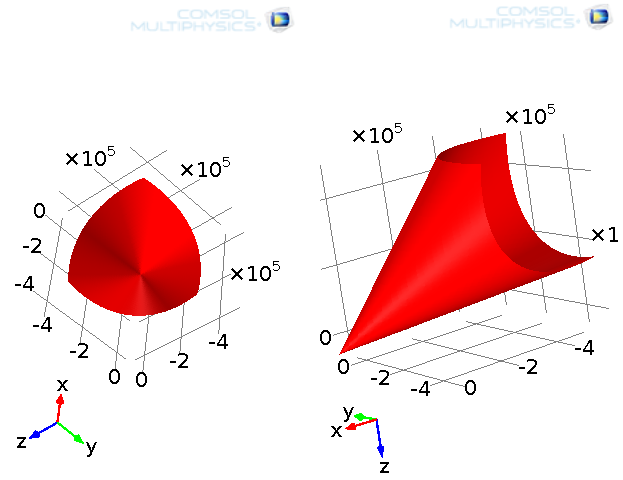
Drucker-Prager 屈服函数表示法。
COMSOL Multiphysics 中土壤塑性的非关联流动法则
接下来,我将向您展示如何借助 COMSOL Multiphysics 对土壤塑性使用非关联法则。针对软件的任意一种塑性模型,都可以使用非关联塑性法则。
如果您选择 Mohr-Coulomb 模型,有两种不同的基本方法可解决非关联塑性。由 Drucker-Prager 模型和Mohr-Coulomb 屈服函数可得到相同的塑性势,但是其静压轴斜率不同,即膨胀角取代了摩擦角(如以下截图所示)。
此外,当使用 Drucker-Prager 模型与 Mohr-Coulomb 准则进行匹配时,可以轻易地将膨胀角与您所需的非关联法则进行匹配。例如,可通过膨胀角为零来求解上述非关联法则。
最后要说明的一项要点是,我们开发了一种名为椭圆端盖的实用特征来避免材料超出特定压力范围的非物理行为。事实上,真实材料维持弹性变形的压力范围并不是无限的。因此,我们可以使用 COMSOL Multiphysics 中的椭圆端盖特征解决这个问题。
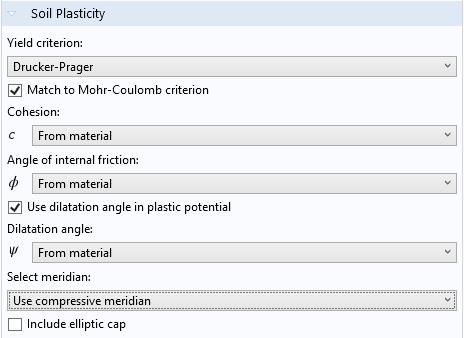
土壤塑性特征设置窗口。
让我们利用目前学到的所有知识来分析隧道开挖实例。同时,我们也将借此机会找出上述不同特征所产生的效果。
隧道开挖实例
为避免建设过程中的塌方事故,工人需对隧道进行必要的加固。隧道开挖过程的模拟,对所需加固量的预测非常重要。
以下模型用于对隧道开挖过程中的土壤行为进行模拟。对不同土壤模型中的地表沉降(即沿自由地表的垂直位移)及塑性区域进行计算和对比。我们将要用到的几何结构如下图所示。为了让我们的模型更加逼真,我们可以使用无限元来扩大土壤区域,同时保持足够小的计算区域,以便在相对较短的时间内找出解决方案。
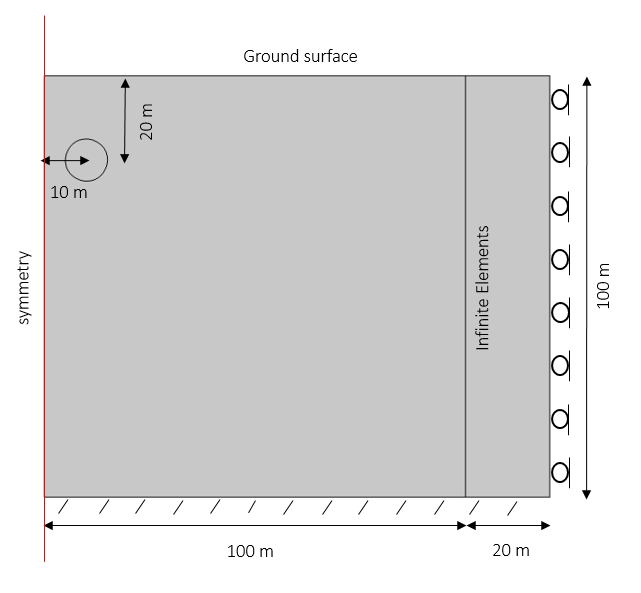
该几何结构由 100 米深和 100 米宽的土壤层及另加 20 米的无限元构成。一条直径为 10 米的隧道位于离对称轴 10 米远、离地表 20 米深的位置。
首先,需要在隧道开挖前在土壤中加入地应力。然后,我们可以计算在移除与隧道对应的土壤后的塑性行为。地应力须被并入第二步。这些操作可以直接在 COMSOL Multiphysics 中进行设置。
我们可以从添加一个计算地应力的固定步骤开始。然后,在第二步中添加土壤可塑性特征,并进行相同的计算步骤。最后,我们可以计算出结果。为了在第二步中加入预应力,我们可以在固体力学界面中加入预应力和应变特征,如下图所示。
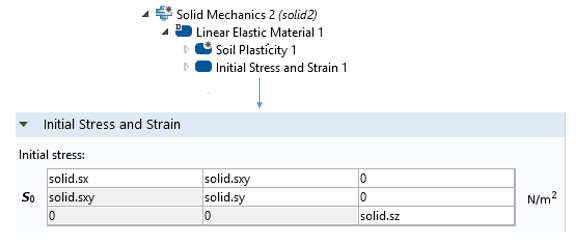
预应力和应变特征用于在隧道开挖时将第一步中的地应力作为预应力加入第二步中。变量 solid.sx 及 solid.sxy为应力张量的 x-分量及 xy-分量,其他参数也是如此。
第一幅图显示了由第一步计算得出的地应力。这些应力来自重力荷载。
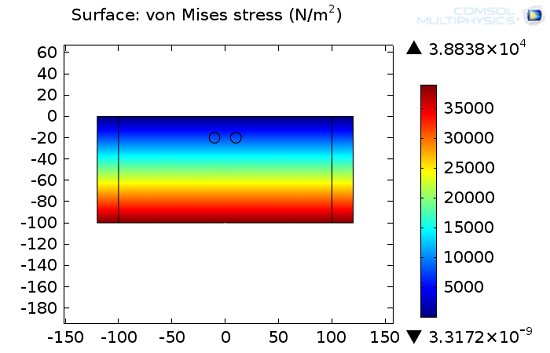
隧道开挖前土壤中的 von Mises 应力。
第二幅图显示了隧道开挖后的应力分布。地应力由第一步计算得出。请注意,如所预见的,隧道周围的 von Mises 应力及隧道形状的变形将会增加。
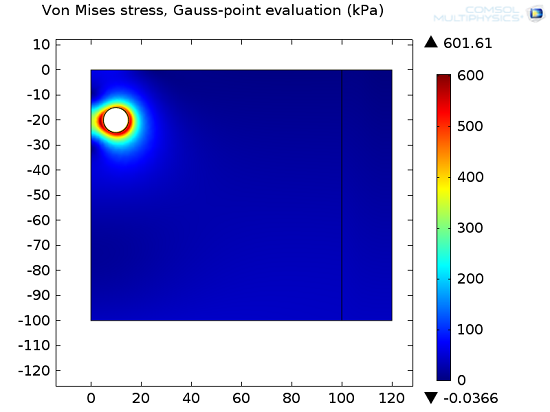
隧道开挖后土壤中的 von Mises 应力。
如上所述,在移除隧道区域时会增加一个塑性特征,且土壤会经历一个塑性行为。如下图中带有关联塑性流动的 Drucker-Prager 模型所示。塑性区域集中在隧道周围。对此区域的分析有助于深入研究导致土壤更容易发生变形的情况。因此,这有助于我们得出避免坍塌所需的加固量和所需的隧道形状。
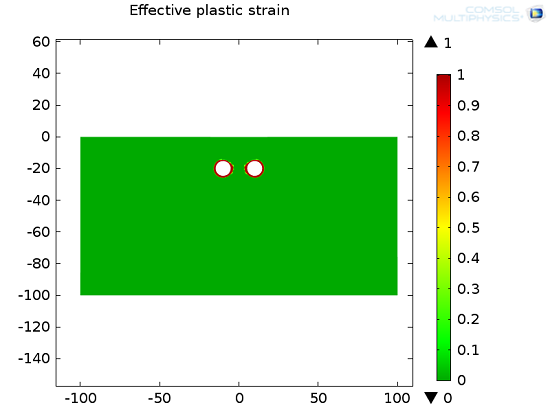
隧道开挖后的塑性区域。
我们对四种不同情况下的隧道开挖进行了仿真,以比较上文所述的不同土壤模型,以及研究内聚力对土壤行为的影响。其结果以地表沉降作为标准。
接下来,我们用一个一维绘图来展示以下结论:内聚力越低,变形越大。需要注意的是,Mohr-Coulomb 模型中的土壤比 Drucker-Prager 模型中的土壤更坚硬。带有零膨胀角的非关联准则防止了土壤在压力下膨胀,因此地表沉降愈发严重。
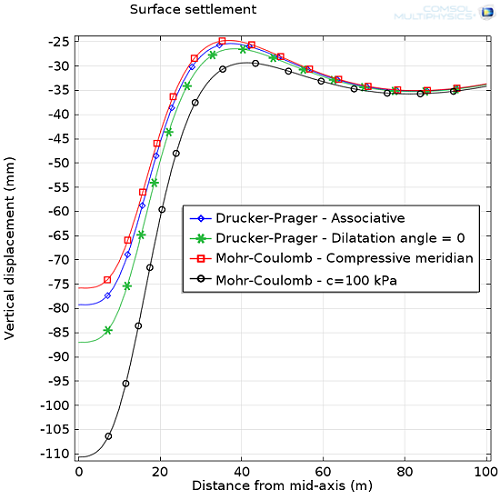
不同塑性模型与材料性质下的地表沉降比较。
延伸阅读
在 COMSOL Multiphysics 中还有多种关于土壤、岩石及混凝土的其他塑性模型。请点击以下链接获取更多关于岩土工程仿真及 COMSOL Multiphysics 中岩土力学模块的信息。
同时,请一定观看关于如何建立开挖模型的视频:



评论 (8)
廷江 檀
2021-12-02你好,为什么我设置了膨胀角模型计算还是不收敛,只有弹性阶段,算不到塑性
朝 崔
2022-11-03τ的公式写错了,应该是公式τ=1/2(σ1-σ3)cosΦ
Kaixi Tang
2022-11-09 COMSOL 员工您好感谢指正,图片公式会尽快修改,谢谢。
光智 任
2024-05-16你好,我想我们请问下咱们软件进行隧道开挖是使用的活化,但是根据其他软件经验,活化实质上就是弹性模量的软化,因此想尝试弹性模量的软化法,但是在第一步中计算的初始应力使用预应力与预应变在软化模量法中不发生变化,这种情况该怎么解决呢?
hao huang
2024-05-16 COMSOL 员工感谢您的回复,对于您提到的问题需要结合具体的模型才能判断,可以发送至技术支持:support@comsol.com,工程师会根据具体模型分析。
光智 任
2024-05-22您好,感谢您的回复。我是在官网案例上的隧道开挖一例进行改进尝试的,除了上述提到的地应力平衡不改变的问题,发现在最后E减小到无线趋近于零的时候出现用于查找弹塑性应变变量的迭代未收敛的错误,这种情况不知道该怎么解决呢?期望收到您的解决答复。
hao huang
2024-05-22 COMSOL 员工感谢您的评论,对于不收敛的问题涉及的原因较多,暂时无法从以上描述给出相关合理的建议,可以将你的模型及问题发送至技术支持:support@comsol.com,工程师会根据具体模型分析。
奥辉 周
2024-08-01您好,软化模量法您最后实现了吗