陀螺仪动力学的模拟

前几天，我儿子第一次接触到了有关旋转体的运动方程，他回来后问了我几个很有意思的问题。这些问题把我带回了多年前学习力学的时光，当时我也曾有过类似的困惑。在今天的博客 中，我将介绍两个与陀螺仪和陀螺有关的 COMSOL Multiphysics 模型，它们很好地展示了旋转体的一些显著特征。

陀螺仪是什么？

陀螺仪最早于 19 世纪中期由 Léon Foucault 提出，发明近 200 年来，它已成为一个重要的科学和工程仪器。陀螺仪的前身陀螺从古代起就已经存在，人们把它看作玩具、用于赌博，或是一种带有魔法属性的物体。

作为一项科学仪器，陀螺仪一直因其在测量和定向方面的精度而备受行业重视。也因此，人们将陀螺仪用于飞机、航天器、潜艇以及惯性制导系统的传感器中。

第一代陀螺仪的复制品。

经典陀螺仪主要基于角动量守恒定律。当不存在外部力矩时，旋转体总希望能维持它的轴取向。当受到扰动，取向改变的阻力主要基于角动量，即角速度与质量惯性矩的乘积。当向转子施加一个不平行于旋转轴的力矩时，受到的影响将非常大。

注意： 现在存在多类陀螺仪，虽然它们基于不同的物理属性，但设计初衷与经典陀螺仪相同。物理及微尺度工程方面的最新进展促成了这一切的实现。

如 下图所示，陀螺仪包含一个被强制以较高角速度绕轴旋转的圆盘。轴通过轴颈连接到名为平衡环的内环上。内平衡环 通过另外一对轴颈连接至外平衡环。这对轴颈包含一个与旋转杆呈直角的轴。第三对轴颈将外平衡环连接至框架。因 此，转子包含三个旋转自由度，每个轴包含一个自由度。注意：框架将被连接到周围环境中（例如，容器）。

如果框架绕任意轴旋转，转子轴将会努力维持它的方向。在此过程中，两个平衡环被迫发生旋转。

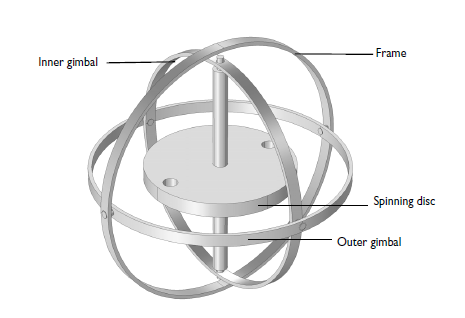
经典陀螺仪示意图。

在 COMSOL Multiphysics 中模拟陀螺效应

我们借助 COMSOL Multiphysics 的多体动力学模块模拟了陀螺仪的机械属性。我们的陀螺效应教学模型就关注了此类研究。接下来将讨论的示例其实包含两个模型：陀螺仪和陀螺。

陀螺仪模型

让我们先从陀螺仪模型开始。模型几何包含四个刚体：转子、两个平衡环和一个框架。转子的材料为钢，其他零件为铝材质。因为材料选择的关系，转子的惯性矩相对 要大于支撑框架。在框架上施加一个绕轴的指定旋转，该轴与转子轴呈 90° 角，并与两个平衡环的轴颈中心线呈 45° 角。框架旋转呈简谐形式，幅值为 2 rad，频率为 2 Hz。每个轴颈均作为一个铰接模拟。

我们分析了两种不同的情况，用于说明转子旋转对取向的影响。第一种情况，转子不旋转。第二种情况，为转子指定 350 rad/s (3342 RPM) 的初始角速度旋转。

下方的第一个动画显示了转子不旋转时，它的取向如何被强制改变。问题中不存在重力，而且从运动学角度讲，转子能够维持它的朝向，因此系统的刚体动力学造成了转子取向的改变。第二个动画中，我们可以看到旋转的转子基本能维持它的取向。

下 图绘制了转子轴的倾角曲线，并显示了稳定性的差异。在精密仪器中，即使旋转时只产生了 1° 的角度误差仍然不可接受。不过，我们可以通过更改设计来减小这类偏差。在我们的示例中，框架的旋转速率非常高。框架会在 0.25 s 内旋转到接近 115°，然后转回，仿真重点研究了这一过程。为了改进轴取向在受到外部干扰时的稳定性，将需要更高的转子速度或更重的转子。

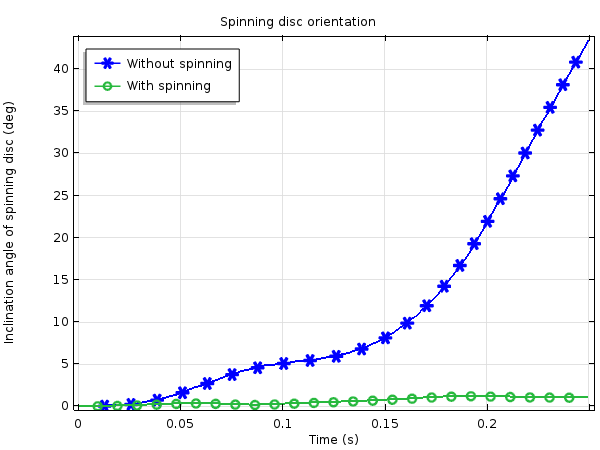
对比有旋转及无旋转时转子轴的倾角。

陀螺模型

我们现在将关注点焦点转到螺模型。这里只用到了单个刚体：即之前示例中的转子。转子轴的初始取向与纵轴呈 20° 角，并引入重力载荷。此外，还为转子指定了一个绕本身轴的初始角速度。底部反作用力和重力载荷共同作用产生了一个指向转子轴和纵轴所成平面之外的力矩。

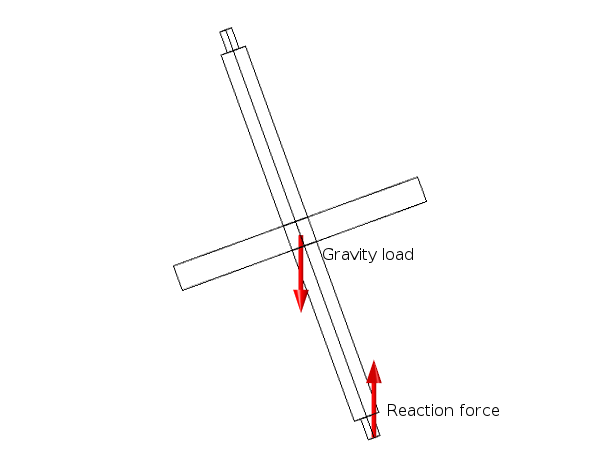
作用在陀螺上的耦合力。

力矩会造成一个指向平面外的角加速度，陀螺的取向开始改变。陀螺取向的改变和绕自身轴的旋转，会在陀螺上造成一个陀螺仪扭矩。在陀螺仪扭矩的影响下，陀螺顶点会缓慢沿一个环形的路径移动。我们将转子轴朝向的这类旋转称作进动。下图显示了轴端点的轨迹。

正如我们观察到的，较宽的环形路径被较小的周期性扰动覆盖，这一运动被称作章动。章动依赖于初始条件。由于对陀螺的研究只是从绕转子轴的一次旋转开始，不存在进动速度，初始条件与纯进动运动不兼容。在真实的物理系统中，随时间的继续，阻尼将减少章动的幅度。

结束语

当您希望求解此类问题时，限制分析中使用的时间步长非常重要。一般而言，应该将时间步长限制为每步长仅对应于几度的旋转角。上例使用了 0.1 ms 的时间步长，对应于转子在一个时间步长绕轴旋转大约 2°。

您可以在 App 库中下载陀螺仪动力学教程模型。如果您对另一项 MEMS 陀螺仪设计技术感兴趣，不妨再学习压电速率陀螺仪教程模型。