通过符号微分加速模型收敛

你是否知道 COMSOL Multiphysics^® 软件内置了一个符号微分求解器，在设置和解决非线性问题时会自动启用？此功能可确保软件在求解此类模型时具有很高的可靠性，但也要付出一些代价。今天，我们将通过几个不同的示例演示此功能，并研究其优点和弊端。

利用符号微分求解简单的非线性问题

让我们从一个相对简单的、单自由度的非线性问题（隐式方程）开始：

其中， T 表示系统的集总温度，Q 代表热载荷，上式当中的分母 (1+T^2/100) 代表系统热导率。

要求解参数 Q 的不同值，我们可以通过阻尼牛顿法找到非线性问题的解，该方法可以通过在 COMSOL Multiphysics 中写残差来完成：

然后将其输入全局方程 接口，如下截图所示。

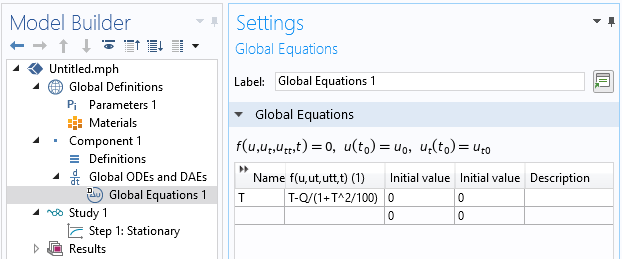
用于求解非线性方程的全局方程接口。

如下图所示，我们可以针对一系列不同的 Q 值来求解此方程。

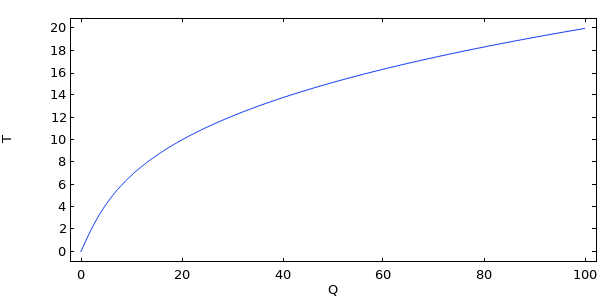
单自由度非线性问题的解。

为了便于说明，我们在下图中画出了 T 取值范围内和选定值 Q 的残差。零交叉处的点是上图的解。

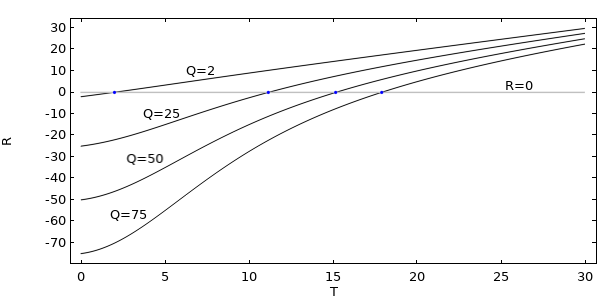
不同参数 Q 值的残差图。与零交叉的 T 值就是非线性方程的解。

我们还画出了相同范围 T 的和 Q 值下的残差的对应导数(雅可比矩阵)。

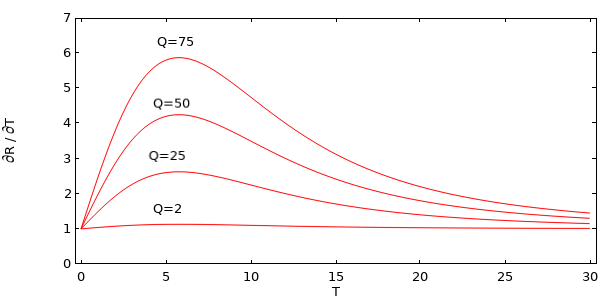
不同 Q 值的残差的导数图。

我们看到，随着 Q 值的增加，雅可比矩函数非线性增强。我们也可以（对于这种简单情况）手动写出其导数：

请记住，软件能够自动通过符号微分获得此导数，并在牛顿步骤中使用它。

可以看出，正是残差第二部分的分母使该表达式有些复杂（回忆下，该项可以被认为是系统的热阻）。事实证明，如果我们愿意，可以忽略该项，通过 nojac() 算子包裹分母的该项：

R(T) =(T – Q/nojac(1+T^2/100))

并修改全局方程，如下截图所示。

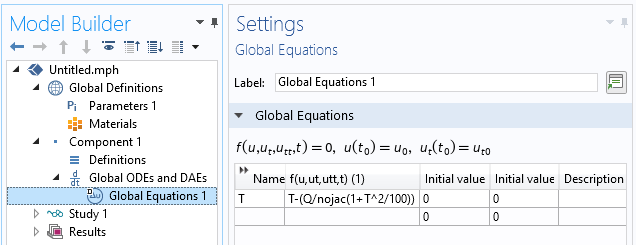
屏幕截图显示了如何使用 nojac() 算子。

结果，符号微分求解器将忽略 nojac() 算子中的所有内容。也就是说，该算子中的项对雅可比矩阵没有贡献。关于 T 的残差导数现在简化为：

通过检查我们可以看到，这种简化的导数仅是 Q 为低值时的一个很好的近似。但是求解器不能对所有的 Q 值，都收敛到解。因此，我们通过避免获取某些项的导数（在这种情况下非常小）使问题变得更简单了，但是在某些情况下会使问题无解。

在 COMSOL Multiphysics^® 中使用 nojac() 算子

我们考虑一下可以使用 nojac() 算子的其他几种方式。

如果我们将全局方程写为：

R(T) = nojac(T – Q/(1+T^2/100))

那么导数将恰好为零，并且这个问题根本无法求解，因此这种情况并无不有趣。

我们还可以尝试将 nojac() 仅应用于一个项：

R(T) = T – Q/(1+nojac(T)*T/100)

现在，我们的导数是：

该导数非常接近于精确的残差，并且至少在这种情况下，即使采用雅可比矩阵公式的这种近似值，求解器将收敛于所有的 Q 值。尽管计算成本没有下降，但这里值得注意的一点是，我们可以将 nojac() 算子应用于残差项的任何子集。

那么，到目前为止我们学到了什么？

1. 您可以使用 nojac() 算子来忽略对雅可比矩阵产生贡献的项
2. 忽略项将影响非线性求解器的收敛
3. 忽略项可减少计算模型的大小

但是，在这个小例子中，最后一点并不是很明显。

减少大型非线性模型的大小

现在让我们看一个更大的三维模型。我们求解了一个边长为 1cm 的正方体上的传热问题，并在此部分上应用了一个极细 网格，从而我们获得了一个较大的模型；自由度大约为 300 万。

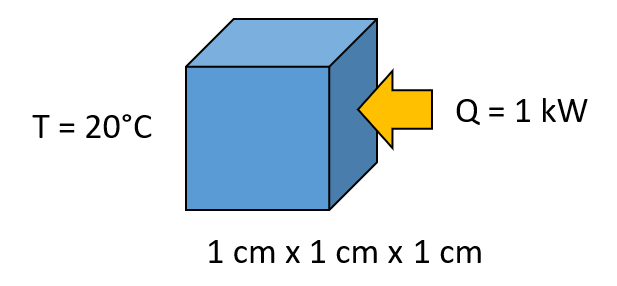
一个用于研究极细网格的简单传热问题的示意图。

我们还将材料特性定义为温度的函数，并使用类似于我们已经看到的材料特性，通过用户自定义的表达式来定义材料的导热系数：

(1+(T[1/K])^2/100)[W/m/K]

可以直接在物理场接口中完成此操作，如下截图所示。

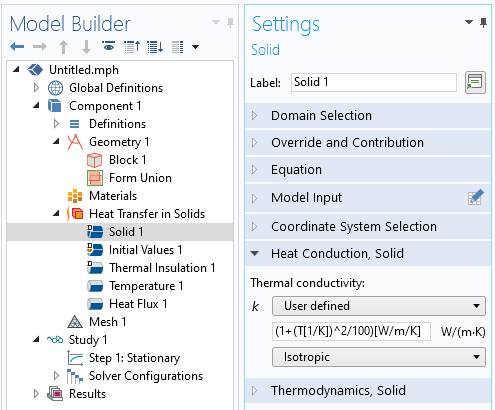
手动将导热系数定义为温度的函数。

当我们使用所有默认设置解决此问题时，该模型将需要用阻尼牛顿法进行四次迭代来求解。整个过程需要大约 135s 的计算时间，并且在一台典型的台式计算机上使用超过 12GB 的内存。在求解过程中，我们还会在日志中收到一条消息，内容为：

找到非对称矩阵。

该消息是材料属性中与温度相关项的结果。也就是说，材料属性中的非线性项使雅可比矩阵不对称，因此该模型将需要更多的内存来求解。现在让我们将整个材料属性表达式包裹在 nojac() 算子中：

nojac(1+(T[1/K])^2/100)[W/m/K]

重新运行该模型，我们看到该模型仍会收敛，需要大约 10GB 内存求解，但现在需要五次默认阻尼牛顿法迭代。也就是说，内存需求下降了，但是收敛的迭代次数却增加了。最有趣的是，执行求解时间为 125s，比以前少了一点！为什么会这样？求解器需要更多的迭代来收敛，但是每次迭代花费的时间更少，因为雅可比矩阵是对称的，需要处理的数据更少。

因此，在这种情况下，尽管需要更多的迭代才能收敛到解，但使用 nojac() 算子既可以减少运行求解时间，又可以减少所需的内存！还要注意，因为使用更新的材料特性表达式，仍然可以正确评估材料特性本身，所以我们能够收敛于相同的解，

避免非局部耦合项

再看最后一个示例：如下图所示，压碎包含可压缩气体的薄壁容器。可以使用结构力学模块中可用的壳公式进行建模。

装有可压缩气体并施加有外部压碎载荷的薄壁容器。

通过利用对称性，我们可以将模型缩减为完整模型的1/8。我们施加近似于压碎的分布载荷，以及代表内部可压缩气体的压力载荷。为了表示可压缩气体，类似于在充气超弹性密封条压缩示例中所做的，我们使用了计算变形容器体积的方法。也就是说，通过使用积分耦合算子，我们在容器的整个表面上施加均匀的压力载荷，并且该压力是基于整个容器的变形来计算的。

这种非局部耦合的作用是，容器每个部分的变形都会影响压力，而压力会影响到各处的变形，因此我们的雅可比矩阵变得非常密集。使用默认的极细网格设置求解此问题时，该模型将花费大约 12GB 的内存和 400s 的时间来求解此具有约 22000 个自由度的模型。

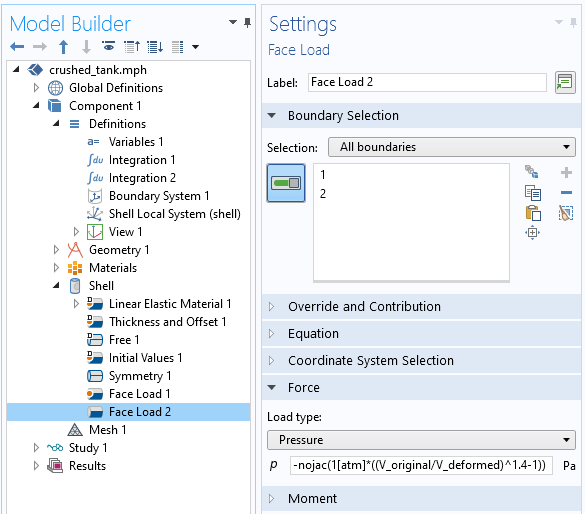
屏幕截图显示了压碎容器模型中修改后的压力。

但是，通过简单的将 nojac() 算子包裹到我们所施加的压力上，我们就可以忽略非局部耦合，从而降低内存需求和求解时间。这样，我们只需要 3GB 的内存和 10s 即可收敛到相同的解！

结论

默认情况下，COMSOL 软件将始终采用精确的雅可比矩阵，因为这可以提供最大的收敛可能性。通常，我们宁愿牺牲一些时间和内存来获得尽可能可靠的解。但是，我们确实有能力和灵活性来忽略雅可比矩阵中的选定项。如果要使用此功能，我们必须显式修改材料属性，修改基本的控制方程或在模型内编写自己的变量表达式，因此这是一个有点高级的用户功能。

当然，使用此功能将近似于雅可比矩阵，这有时会减慢甚至阻止收敛，因此在这种情况下请不要使用它。但是，如果模型应用 nojac() 算子时确实收敛，收敛于完整雅可比矩阵计算相同的解，并且可能会使用更少的时间和内存，那么在构建复杂的多物理场模型时，这是一个很好的特性。