基于方程建模 博客文章
如何在 COMSOL Multiphysics® 中计算几何对象间的距离
2017年 3月 2日
如何在 COMSOL Multiphysics® 中计算两个变形的几何对象之间的距离？欢迎阅读文章。
利用基于方程建模求解浅水波动方程
2017年 2月 21日
浅水波动方程是基于方程建模的案例之一。在COMSOL Multiphysics® 中，您可以定义表达式来求解浅水波动方程，借此分析海岸侵蚀问题。
通过仿真 App 了解 FitzHugh-Nagumo 模型的动力学原理
2016年 10月 7日
1961 年，R. Fitzhugh (参考文献1) 和 J. Nagumo 提出了一个模型，用于模拟在生物体的可兴奋细胞中观察到的电流信号。
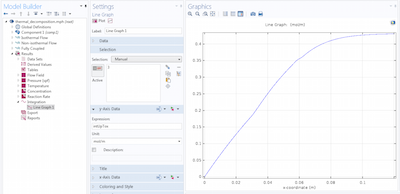
变化极限的积分和求解积分微分方程
2016年 10月 6日
学习如何分析变化极限的空间积分，无论它们是明确指定的还是隐式定义的。(第二部分，共2部分)
基于方程的轴对称组件建模指南
2016年 10月 5日
柱坐标系对于高效求解和后处理旋转对称问题而言很有用。COMSOL Multiphysics® 软件为轴对称物理场接口中的柱坐标系提供了内置支持。当您使用数学接口对定制的偏微分方程（partial differential equation，简称 PDE）进行定义时，请务必仔细辨明它们的意义。
探究图灵的形态发生理论
2016年 5月 9日
你是否思考过老虎身上的条纹究竟是怎样形成的？艾伦·图灵（Alan Turing）的形态发生理论提供了一种可能的解释：条纹一类的图案最初呈均匀状，逐渐自然地演变成有规律的图案。今天，我们将详细讨论图灵的形态发生理论，并探讨一些现代研究，其中涉及了 COMSOL Multiphysics 中的分支形态发生建模。
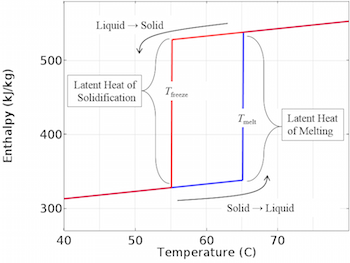
具有滞后的相变材料的热建模
2016年 3月 24日
当一种材料的熔化温度与凝固温度不同时，就会出现滞后现象。我们在此演示了这种材料的热建模。
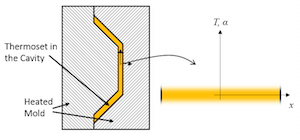
模拟热固化过程
2016年 3月 16日
热固性树脂的聚合是热固化的一个例子，这是一个由温度引起材料发生化学变化的过程。
