基于方程建模 博客文章

求解延迟微分方程模拟土拨鼠?
从 COMSOL Multiphysics® 6.3 版本开始,你可以对延迟微分方程进行建模。让我们通过一个独特的案例来探索这项新功能。

捕蚊器真的有用吗?通过粒子追踪法预测捕蚊器的性能
你是一个蚊子吸引者吗?让我们用基于方程的建模来模拟一个有趣的场景,探索蚊子是喜欢捕蚊器还是喜欢人的皮肤。

使用 COMSOL® 进行衍生式设计以获得新灵感
一个新的设计是源自人还是过程?我们可以想象一个新设计的产生过程:首先设计师先有一个设想,然后拿起铅笔把他的想法变成现实。当然,今天的设计师和工程师可能不使用铅笔,也可能没有一个最终的设计想法。

为什么高尔夫球有凹痕?
高尔夫球为什么会有凹痕?我可以用 COMSOL Multiphysics 模拟高尔夫球吗?我可以使用仿真来优化我的击球并打出标准杆吗?下面带大家找出这些问题的答案。

使用 COMSOL Multiphysics® 进行微磁仿真
中国复旦大学的余伟超博士使用 COMSOL Multiphysics® 中的“物理场开发期”创建了一个“微磁模块”,用于执行微磁模拟。
如何使用 COMSOL® 模拟代谢反应网络
某些冰淇淋、布丁和糖果具有非常鲜艳的黄色,这种黄色来自维生素 B2。 该补充剂的制造是代谢反应网络的一个例子……

将自适应网格细化与数据过滤相结合
在我们之前关于数据过滤的博客文章的后续文章中,我们演示了如何为具有非均匀热负载的热模型实现自适应网格细化和亥姆霍兹滤波器。
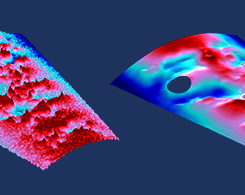
通过数据滤波提高模型性能
想要在您的模型中包含实验数据作为负载或边界条件,但数据随空间或时间变化并且有噪声? 尝试实现数据过滤,例如亥姆霍兹过滤器。

将全局方程引入全耦合目标搜索法
今天,我们将在 COMSOL Multiphysics® 软件的模型中引入一个目标搜索方程,该方程与全耦合方法结合使用可以求解非线性问题。在计算上,尽管这种方法比我们之前介绍的分离式求解方法成本更高,但其在鲁棒性方面却具有一些独特的优势,并能够突显 COMSOL® 软件的一个核心优势。

将目标搜索的方法引入分离式求解器
分离式求解方法是 COMSOL Multiphysics® 软件的核心技术之一,它可以快速求解非线性多物理场(和单物理场)问题得到收敛解。你是否知道?我们还可以通过引入一个额外的全局方程来扩充这个求解方法,其中,全局方程能用于调整模型输入来实现所需的输出。

基于方程的时间空间离散建模
在 COMSOL Multiphysics®中,计算模型中的几乎任何表达式都可以修改。例如,使用时间空间离散化可以使优化问题易于快速实现。
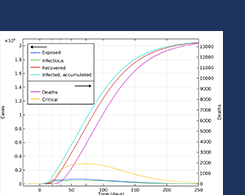
使用 COMSOL Multiphysics® 模拟 COVID-19 的传播
从易感者,暴露者,感染者到恢复者:了解数值模型如何帮助我们了解COVID-19大流行的动态及其传播方式。
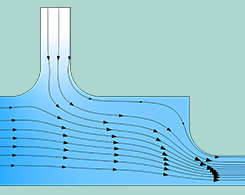
如何使用 PID 控制器插件模拟控制系统
PID 控制器可用于多种行业。这篇博客文章演示了如何在两个仿真示例中轻松合并 PID 控制器插件。
使用 COMSOL Multiphysics® 优化 PID 控制器性能
想象一下,你正在公路旅行,以每小时 60 英里的速度在公路上行驶。为了保持这个速度,你决定打开巡航控制。毕竟你正在度假——为什么不让汽车替你干活呢?无论你是上坡还是下坡,汽车都会对速度变化做出反应,自动加速或减速。

数值积分和高斯点简介
在有限元模型中,你可能会在多种情境下遇到数值积分和高斯点的概念。在本篇博客文章中,我们将讨论在什么情况下,以及为什么使用数值积分。此外,还强调了在 COMSOL Multiphysics® 软件中检查和修改数值积分方案的方法。最后,对高斯点自由度的使用进行了说明。

仿真 App 助力 ABB 牵引电机公司实现数字化
下面是一个使用COMSOL Server™优化研发过程的真实例子:在ABB牵引电机公司,工程师们在电机设计中使用模拟应用程序来分析CFD和热量。

在 COMSOL® 中对移动载荷和约束进行建模的 3 种方法
了解在 COMSOL Multiphysics® 中模拟移动载荷和约束的 3 种方法:使用变量、插值函数和从 CAD 几何图形导入的路径。

非标准约束和弱贡献的力量
为了以灵活且独立于物理场的方式扩展 COMSOL Multiphysics® 软件的适用性,您可以使用所谓的弱贡献来实现非标准约束。

如何在 COMSOL 中实现瞬态方程的弱形式
了解如何使用 COMSOL Multiphysics® 的基于方程的建模功能实现弱形式来求解瞬态问题。

图像去噪以及其他多维变分问题
通过一个有趣的例子,学习如何解决具有多维度、高阶导数和多个未知数的变分问题:在粒状照片中的图像去噪。

实现不等式约束的方法
学习 2 种在变分问题中强制执行不等式约束的方法,即拉格朗日乘子法和增广拉格朗日法,以及它们背后的理论。

强制约束中数值问题的处理方法
在本系列博客的第一部分,我们讨论了如何通过简单的边界条件解决变分问题。接下来,我们将进行更复杂的约束,并使用拉格朗日乘子建立等效无约束问题。今天,我们讨论约束执行的数值问题。拉格朗日乘子法在理论上是精确的,但是在数值解的应用却有一定的挑战性。

在变分问题中指定边界条件和约束
在本博客系列的第一部分中,我们讨论了变分问题,并演示了如何在 COMSOL Multiphysics® 软件中使用简单的内置边界条件解决它们。今天,我们将讨论更通用的边界条件和约束,并展示如何使用第一部分(皂膜)中的相同变分问题以及同样的数学方法,在 COMSOL® 软件中实现这些边界条件和约束。

肥皂膜及其他变分问题建模概述
肥皂膜、悬链线电缆和光束有什么共同点?它们都有着使某些数量最小化的行为方式,这类问题普遍存在于生物学、经济学、弹性理论、材料科学和图像处理等科学和工程领域。
