基于方程建模 博客文章

追波逐浪:罗素的故事和 KdV 方程
在 1830 年代的苏格兰,约翰·斯科特·罗素 (John Scott Russell) 注意到一条波浪在浅水运河中表现得很奇怪。 他先是骑马追浪。 然后,他为之奉献了一生。

含热粘性损耗的声学拓扑优化
来自丹麦 GN Hearing 公司的特邀博主探讨了如何在助听器、手机和超材料几何结构等微型声学装备的拓扑优化中加入热粘性损耗。

通过仿真预测地下水中的溶质迁移
为了使地下水能够用于灌溉和饮用,我们需要了解各种溶质如何在水中迁移。地下水流模块包含模拟这些应用的功能。

COMSOL Multiphysics® 中基于方程建模的3个示例
COMSOL Multiphysics® 软件提供了基于方程的建模功能,该功能带来的可能性包括但不限于:创建可以保存和共享的新物理场接口,修改模型的基础方程,以及模拟更多类型的设备和过程。

如何生成随机非均匀材料数据
你知道有一种方法可以将具有由谱密度分布决定的指定统计属性的随机材料数据,用于生成和可视化结果吗?

如何在 COMSOL Multiphysics® 中生成随机表面
获得在 COMSOL Multiphysics® 中生成随机表面(如粗糙表面和微结构)的全面背景和分步指南。

利用最大值原理节省计算时间和资源
通过利用大型复杂模型中的最大值原理,你将节省时间和计算资源,而不必购买更大的计算机或让你需要一整夜来求解模型。

如何在 COMSOL Multiphysics® 中计算几何对象间的距离
如何在 COMSOL Multiphysics® 中计算两个变形的几何对象之间的距离?欢迎阅读文章。

利用基于方程建模求解浅水波动方程
浅水波动方程是基于方程建模的案例之一。在COMSOL Multiphysics® 中,您可以定义表达式来求解浅水波动方程,借此分析海岸侵蚀问题。

通过仿真 App 了解 FitzHugh-Nagumo 模型的动力学原理
1961 年,R. Fitzhugh (参考文献1) 和 J. Nagumo 提出了一个模型,用于模拟在生物体的可兴奋细胞中观察到的电流信号。
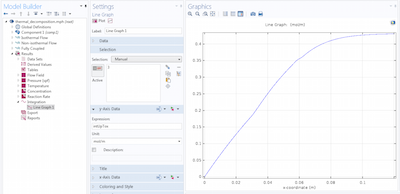
变化极限的积分和求解积分微分方程
学习如何分析变化极限的空间积分,无论它们是明确指定的还是隐式定义的。(第二部分,共2部分)

基于方程的轴对称组件建模指南
柱坐标系对于高效求解和后处理旋转对称问题而言很有用。COMSOL Multiphysics® 软件为轴对称物理场接口中的柱坐标系提供了内置支持。当您使用数学接口对定制的偏微分方程(partial differential equation,简称 PDE)进行定义时,请务必仔细辨明它们的意义。

探究图灵的形态发生理论
你是否思考过老虎身上的条纹究竟是怎样形成的?艾伦·图灵(Alan Turing)的形态发生理论提供了一种可能的解释:条纹一类的图案最初呈均匀状,逐渐自然地演变成有规律的图案。今天,我们将详细讨论图灵的形态发生理论,并探讨一些现代研究,其中涉及了 COMSOL Multiphysics 中的分支形态发生建模。
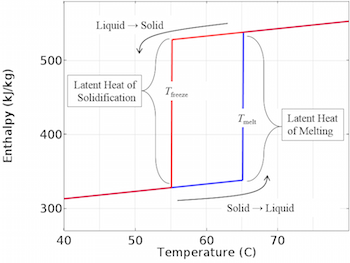
具有滞后的相变材料的热建模
当一种材料的熔化温度与凝固温度不同时,就会出现滞后现象。我们在此演示了这种材料的热建模。
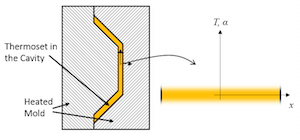
模拟热固化过程
热固性树脂的聚合是热固化的一个例子,这是一个由温度引起材料发生化学变化的过程。

借助仿真模拟流行病的传播
我想您一定记得上次因流感而卧床的情景。流感俗称感冒,这对我们而言可能只是一次很不愉快的体验,但其实它每年还会造成大量的人员伤亡。现在,公共卫生官员正借助数学仿真技巧研究流感和其他传热性疾病,希望能预测它们的传播,并据此做出明智的公共卫生决策。

借助虚构解方法验证仿真
我们该如何检验仿真工具是否正确工作?方法之一就是虚构解方法。该方法涉及假设一个解,获取与假设一致的源项及其他附加条件,使用上述条件作为模拟工具的输入项来求解问题,以及对比结果与假设解。该方法使用简单且用途广泛。例如,桑迪亚国家实验室的研究人员将该方法与一些内部代码一同使用。

借助 COMSOL® 仿真 App 执行弱形式
在之前的弱形式系列博客中,我们对弱形式方程进行了离散,希望得到可用于求解我们简单示例问题中未知系数的矩阵方程。按照博客“在 COMSOL Multiphysics 中执行弱形式”中的步骤操作,我们将能在 COMSOL Multiphysics® 软件中执行该方程,并能加入其他步骤来检查矩阵。我们还发现可以借助 COMSOL® App 更轻松地实现所有相关矩阵的同时展示,并能在同一个屏幕上按类排列。

我们能听出鼓的形状吗?
半个世纪前,Mark Kac 做了一个有趣的讲座,讲座内容基于十年前他从 Bochner 教授那听到的一个问题:“我们能听出鼓声的形状吗?”他把讲座的重点放在特定的(待定)一组特征值能否确定振动鼓膜形状。特征值问题已经解决了,在这里,我们通过考虑一些有趣的物理效应,探索这个问题中“听”的部分。

弱形式方程的离散化
本博客是弱公式化系列博客的后续部分。在之前的博客中,我们使用 COMSOL Multiphysics 软件设置并求解了一个典型的弱形式方程,并借助一些简单的物理参数验证了结果。今天我们将深入了解这些方程是如何被离散并数值求解的。

在 COMSOL Multiphysics 中执行弱形式
这篇博客是弱形式系列博客的组成部分,旨在帮助用户在最小的先决条件下理解弱形式。在第一篇博客中,我们学习了弱形式的基本概念。所有方程停留在解析形式。今天我们将使用 COMSOL Multiphysics 仿真软件来从数值上求解上述方程。我们在此强烈建议您打开 COMSOL 软件,随我们一起操作。

弱形式概述
该篇博客将简要介绍弱形式,旨在为没接触过有限元分析和矢算、但对弱形式又有浓厚兴趣的用户提供一些物理及积分方面的基础知识。

利用基于方程的建模理解交通拥堵
我们都曾因为堵车而感到无聊和沮丧。通常,交通堵塞的出现或消失都没有明显原因。我们利用气体动力学类比法,同时使用 COMSOL Multiphysics 基于方程的建模功能模拟了交通流,希望能更好地了解为什么会出现交通堵塞。

使用 COMSOL 理解稳定性方法
在这里,我们提供了一个质量传输示例模型,以帮助描述稳定方法对您的数值模型的影响。
