简介 博客文章
复合材料模块简介
阅读这篇博客，探索复合材料模块，一个包含模拟层状复合结构的专用功能的COMSOL Multiphysics®附加产品。
使用 COMSOL 模拟蒸发冷却效应
从气象学到食品加工，蒸发具有许多工业和科学应用。 在这里，我们将介绍如何使用传热模块模拟蒸发。
如何创建包含 CAD 导入和选择的仿真 App
在使用 COMSOL 软件二次开发的过程中，你可能会遇到这样的问题：如何使用 App 开发器创建可以处理 CAD 导入并能让用户交互式选择边界条件的仿真 App？我需要了解编程吗？
如何借助浏览器内置的翻译工具查看 COMSOL 文档？
COMSOL Multiphysics® 软件内置了与操作自动关联的在线帮助功能和大量的技术文档。虽然我们正在逐步进行汉化，但是目前很多文档仅有英文版本，对于一些中文用户来说，阅读这些技术文档可能比较费时费力。好消息是，近年来机器翻译在准确度和可读性方面都得到了质的提升，很多主流网页浏览器也内置了机器翻译工具，方便用户在浏览网页时对页面内容进行自动翻译。
在 COMSOL® 中模拟声-结构相互作用
声固耦合（ASI）问题要求对固体中的弹性波，流体中的压力波以及两者之间的相互作用进行建模。ASI 的使用包括有声音的产生，发散，传播或接收的设备，以及用于声音的分配、隔音或消除噪声的机械系统。
通过密度方法进行拓扑优化
工程师在设计飞机和空间应用中的轻量化结构部件时有很大的自由度，因此使用能够开发自由度的方法很有意义。拓扑优化是在早期设计阶段普遍使用的方法。拓扑优化方法通常需要进行正则化和特殊的插值函数才能获得有意义的设计，这对于新手和有经验的仿真用户而言都比较困难。
如何定制 COMSOL Desktop® 和使用键盘快捷键
想要提高建模过程的效率吗？阅读本文，了解如何定制 COMSOL Desktop® 以及各种实用的键盘快捷键，提升你的建模技巧。
课程：定义多物理场模型
在 COMSOL® 软件中建立多物理场模型有 3 种方法：全自动、使用预定义耦合的手动和手动使用用户定义的耦合。 在这里，我们讨论第一种方法。
肥皂膜及其他变分问题建模概述
肥皂膜、悬链线电缆和光束有什么共同点？它们都有着使某些数量最小化的行为方式，这类问题普遍存在于生物学、经济学、弹性理论、材料科学和图像处理等科学和工程领域。
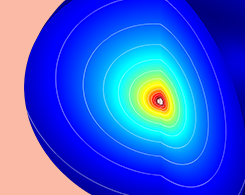
什么是多普勒效应？
救护车或警车迎面驶来，笛声的音调明显增高。虫子游过水坑，水面上荡起一道道波纹。夜空中的星星呈现出红色。以上均为多普勒效应的实例。
COMSOL Multiphysics® 中基于方程建模的3个示例
COMSOL Multiphysics® 软件提供了基于方程的建模功能，该功能带来的可能性包括但不限于：创建可以保存和共享的新物理场接口，修改模型的基础方程，以及模拟更多类型的设备和过程。
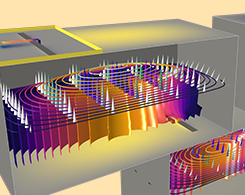
使用电磁仿真设计微波电路概述
避免导致模型运行时间过长和结果不准确的常见 EM 仿真错误。 以下是对射频、微波和毫米波电路进行建模的方法。
使用 COMSOL Multiphysics® 模拟表面反应
在生物物理学、电化学以及催化反应器设计中，研究人员和工程师会利用包含气-固和液-固界面的固体表面的特殊化学与物理性质。本文将讨论简单表面上的表面反应动力学的基础知识，以及如何用 COMSOL Multiphysics® 软件模拟表面反应。在后续博客中，我们将探讨如何描述均质多孔介质表面的质量传递和反应动力学。
非麦克斯韦 EEDF 等离子体建模简介
等离子体建模通常需要了解电子能量分布函数（EEDF）以及电子迁移率和扩散率等传递属性。
应力线性化建模简介
在一些工程应用中，必须通过模拟一组穿过薄结构横截面的应力线性化来近似表示一般的三维应力水平。对于高压容器分析、焊缝疲劳分析以及确定混凝土中的钢筋要求等应用而言，此模拟非常重要。
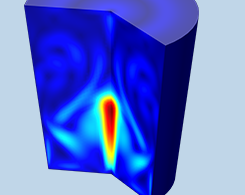
COMSOL Multiphysics® 自然对流仿真简介
自然对流现象存在于电子设备冷却、室内气候系统和环境运输等众多科学与工程应用中。在 COMSOL Multiphysics® 5.2a 版本中，CFD 和传热模块新增的一些功能使建立自然对流模型及其求解变得更加简单。在这篇博客,我们将概述自然对流现象和相关的新功能，并讨论在模拟自然对流时可能遇到的一些问题。
在 COMSOL Multiphysics® 中高效模拟天线
在天线建模过程中，为了保持效率和准确性，我们应该从简单的几何形状开始模拟，然后逐渐添加更多复杂的功能。最终的模拟需要包括足够的细节，以准确表达我们的设计，同时删除那些增加计算成本的、不必要的单元。
非线性弹性材料简介
非线性弹性材料模型的例子:Ramberg-Osgood, Duncan-Chang, Hardin-Drnevich, Power law 等。文中讨论了如何在你的分析中应用非线性弹性材料。
批处理扫描中任务并行的附加值
到目前为止，我们在混合建模系列博客中还没有详细讨论的一件事是，当向我们的计算中增加更多计算资源时，我们可以期待怎样程度的加速。今天，我们考虑一些解释并行计算局限性的理论研究，并将介绍如何使用 COMSOL 软件的批处理扫描 选项。这是一个内置的、易并行计算功能，可在达到极限时提高性能。 Amdahl 定律和 Gustafson-Barsis 定律 我们之前已经提到过的如何通过增加计算单元来提高速度是基于算法的（在这篇文章中我们将使用术语进程，但添加的计算单元也可以是线程 ）。一个严格的串行算法，像计算Fibonacci 数列的元素，完全不能从增加过程中受益，而并行算法，如向量加法，可以利用与向量中的元素一样多的处理器。实际中的大多数算法都介于这两者之间。 为了分析一个算法可能的最大加速，我们将假设它由一小部分完全并行化的代码和一小部分严格串行化的代码组成。我们调用并行代码 \varphi 的分数，其中，\varphi 是介于(包括) 0 和 1 之间的一个数字。这自动意味着我们的算法有一个等于 (1-\varphi) 的串行代码片段。 考虑 P 个活动进程的计算时间 T(P)，从 P=1 开始，我们可以使用表达式 T(1) = T(1) \cdot(\varphi + (1-\varphi))。当运行 P 个进程时，代码的串行部分不受影响，但完全并行化的代码的计算速度将提高P倍。因此，P 进程的计算时间为 T(P)=T(1) \cdot (\varphi / P + (1 -\varphi))，加速度为 S(P):=T(1)/T(P)=1/(\varphi/P+(1-\varphi))。 Amdahl 定律 这个表达式是Amdahl 定律的核心。对于不同的值 \varphi 和 P 绘制图 S(P) ，我们现在在下图中看到一些有趣的东西。 为可并行化代码的不同部分增加进程数的加速比。 对于 100% 并行化代码，极限是不存在的。然而，我们发现对于 \varphi<1，渐近极限或理论最大加速比为 S{max}(\varphi):=\lim{P\to \infty} S(P)=1/(1-\varphi)。 对于 95% 并行化的代码，我们发现 S{max}(0.95)=20，即使我们有无限数量的进程，最大加速也是 20 倍。此外，我们有 S{max}(0.9)=10, S{max}(0.75)=4 和 S{max}(0.5)=2。当减少并行化代码的比例时，理论最大加速比会迅速下降。 但不要现在就放弃回家! Gustafson-Barsis 定律 Amdahl 定律没有 考虑到一件事，那就是当我们购买一台速度更快、内存更大的计算机来运行更多进程时，通常不是想更快地计算之前的小模型。相反，我们想要计算新的、更大（更酷）的模型。这就是 Gustafson-Barsis 定律的全部内容。它基于这样一个假设，即我们要计算的问题的规模随着可用进程的数量线性增加。 Amdahl 定律假定问题的大小是固定的。当添加新的处理器时，它们处理的是最初由较少数量的进程处理的部分问题。通过添加越来越多的进程，我们并没有充分利用所添加进程的全部能力，因为最终它们能够处理的问题大小达到了下限。然而，假设问题的大小随着添加的进程数量的增加而增加，那么我们就将所有进程利用到假设的水平，并且执行计算的加速是无限的。 描述这种现象的方程是 S(P)=\phi\cdot P-(1-\phi)，这为我们提供了一个更为乐观的结果，即所谓的缩放加速（类似于生产力），如下图所示： 当考虑到工作的规模通常会随着可用进程的数量而增加时，我们的预测就更加乐观了。 通信成本 Gustafson-Barsis 定律意味着，我们拥有的能添加到进程中的资源才能限制我们可以计算的问题的大小。然而，还有其他因素会影响加速。到目前为止，我们在这个系列博客中试图强调的一点是，通信成本较高。但是我们还没有谈到它有多贵，所以让我们看一些例子。 […]
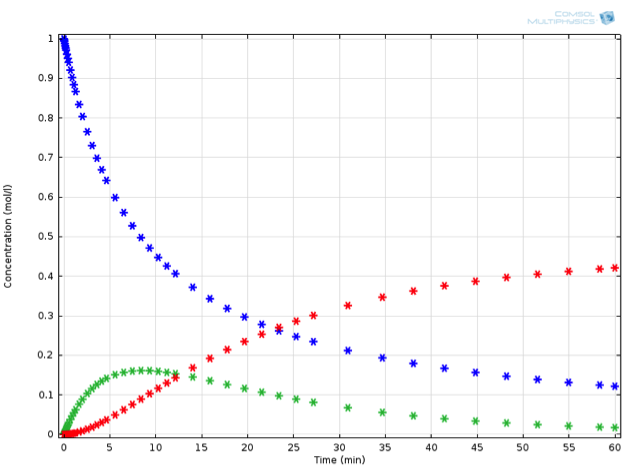
用阿伦尼乌斯方程描述化学反应动力学
无数的复杂情况和陷阱使化学模拟具有挑战性。在这篇博客中，我们对化学动力学和阿伦尼乌斯定律进行了介绍，以提供帮助。