通用 博客文章

主题演讲视频:通过仿真优化电缆系统
电缆为高空飞机、地下矿井和海上风电场提供电力。根据使用情况,电缆的形状、尺寸和环境可能有很大不同——所有这些因素都会影响其性能。

主题演讲视频:EPFL 通过仿真拿下超级高铁大赛冠军
EPFLoop 团队凭借其设计的超级高铁舱站上了 COMSOL 用户年会 2018 洛桑站的领奖台,他们展示的方案让观众们大饱眼福。
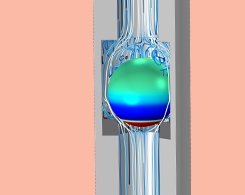
模拟球形止回阀中的流-固耦合作用
在球型止回阀中模拟FSI,找出流量、流体压力和流体速度。COMSOL®软件包含一个预定义的多物理耦合,这使得它很简单。

通过 2 种网格自适应方法实现更高效的计算
网格自适应的目标是通过修改网格实现更高效地求解。通常,我们希望使用尽可能少的网格单元获得精确的解,在不太重要的区域使用较粗的网格,在感兴趣的区域使用较精细的网格。有时,我们甚至可能会考虑各向异性单元。从 5.4 版本开始, COMSOL Multiphysics® 软件包含了一些增强方法以调整网格。这篇博客,让我们来看看如何使用这些方法。 确定所需网格单元的大小 要对网格进行自适应操作,必须知道所需的网格单元大小。然而,找到合适的网格大小并不容易,事实上这需要进行大量的研究。对于稳态和特征值问题,我们可以使用COMSOL Multiphysics 中的 自适应和误差估计 功能基于内置的误差估计自动调整网格。 COMSOL 软件中的网格自适应方法并不局限于使用内置的误差估计,它还具有更高地灵活性。可以先在粗网格上求解一个较简单的问题,然后基于此解通过求解一个表达式来控制较难问题的单元大小。另外,还可以使用导入的插值函数或任何自定义表达式来控制单元大小。 本文不讨论这方面内容,而是假设已经隐式或显式地知道所需的单元大小是 x,y 和 z(三维空间)的函数。也就是说,网格单元的边长由该边中点坐标的函数表达式确定。当然,一般情况下不可能完全满足此要求,即使是一个三角形单元也需要满足三角形不等式。但是,请记住:大小表达式代表空间中每个点所需的单元边长。 根据大小表达式调整网格的 2 种方法 COMSOL Multiphysics 的 网格节点下有 2 种不同的方法可以构建适应大小表达式的网格。 第一种方法,我们可以在网格划分序列中使用大小表达式 属性来改变生成网格的大小。如果使用研究中的网格自适应功能,则相当于选择了 重新生成网格 选项,其中的自由网格生成器(自由三角形网格,自由四边形网格和自由四面体网格)会考虑网格大小。另一方面,例如 映射 、扫掠 和某种程度上的 边界层)会忽略大小表达式属性(根据定义,结构化网格不能遵循大小可变的字段)。简单来说,就是如果我们构建的是结构化网格,可能无法使用此方法。 另一种方法是使用 自适应 操作。此操作通过单元细化和粗化来修改现有网格。我们可以在具有任何单元类型的网格上以及在导入的网格上使用 自适应 操作。这是一种更强大的方法,并且可能更好地遵循指定的大小表达式。但是,结果通常不如从头开始生成的网格平滑。 下面,我们将详细讨论这 2 种方法,并看看二者产生的结果有何不同。 使用大小表达式属性 如前所述,使用大小表达式属性方法通常能获得高质量的网格。但是,如果这种方法产生的单元质量较差(在大小过渡较快时会出现这种情况),则可能无法达到所需的单元大小。有关网格质量的讨论,请阅读博客:如何检查 COMSOL Multiphysics® 中的网格质量。由于每次调整都是从头开始构建网格,因此对于复杂的几何结构而言,此过程可能非常耗时。 使用 大小表达式 属性对一个圆形几何的三角形网格应用大小表达式,得到高质量的网格单元和大小过渡平滑的网格。 如果已知大小表达式(例如,一个全局插值函数),在背景栅格上进行计算通常很方便(上图中的基于栅格计算)。需要确保栅格分辨率足够高,才能捕获大小表达式描述的所有特征。 当大小表达式取决于已知的空间变化量(例如材料),可以使用 初始表达式 计算选项。这样,就可以使用模型中的任何表达式。软件将在求解前计算表达式(与可用于研究步骤的 获取以下步骤的初始值 命令对比)。我们还可以指定某个研究步,因为一些表达式的值取决于研究。 最后,还可以基于现有解计算。内置的 误差 估计使用的是 误差指示器 表达式类型 ,但也可以使用任意的大小表达式,这取决于现有的解决方案。例如,有时可能想在应力较大的地方细化网格。 使用自适应操作 另一种方法是基于现有的网格进行修改来匹配所需的单元大小。这就是 自适应 操作的作用。它适用于所有单元类型,也可作用于导入的网格。它的许多选项和输入字段与 大小表达式 属性相同。 该操作有三种适应方法:最长边细化,常规细化 和 通用修改。前两种细化方法是基于单元边的二等分法操作。由于这些单元边太长,所有现有网格的顶点被保留,因此这些方法无法被粗化。 自 5.4 版本开始,COMSOL Multiphysics 软件内置了 通用修改 方法。顾名思义,就是以非常通用的方式修改网格: 单元可以被细化 […]

主题演讲视频:通过仿真加强 STEM 教育
教师如何提高学生在科学、技术、工程和数学(STEM)本科课程中的学习效果?为了找到答案,美国哈特福德大学教授 Ivana Milanovic 将基于问题的学习(PBL)和基于探究的学习(IBL)相结合,开发了一种基于仿真的方法。

通过密度方法进行拓扑优化
工程师在设计飞机和空间应用中的轻量化结构部件时有很大的自由度,因此使用能够开发自由度的方法很有意义。拓扑优化是在早期设计阶段普遍使用的方法。拓扑优化方法通常需要进行正则化和特殊的插值函数才能获得有意义的设计,这对于新手和有经验的仿真用户而言都比较困难。

如何使用报告模板创建自定义报告
你可以通过报告来记录并显示仿真设置和结果。为了提高这一过程的效率,COMSOL Multiphysics® 提供了有效的工具用于创建易于使用的报告模板。

主题演讲视频:通过仿真 App 改进同步加速器光源
对于同步加速器光源,越亮越好: RadiaSoft LLC 创建并部署了波动光学仿真 App,为同步加速器升级项目设计改进的真空室。

如何定制 COMSOL Desktop® 和使用键盘快捷键
想要提高建模过程的效率吗?阅读本文,了解如何定制 COMSOL Desktop® 以及各种实用的键盘快捷键,提升你的建模技巧。

使用激波管仿真 App 研究激波现象
冲击波过去只是一个理论问题。 然后,冲击管使实验成为可能,但它既昂贵又低效。

主题演讲视频:仿真助力心脏泵设计改进
心力衰竭是一个全球性的健康问题,影响着数百万人,使他们无法正常生活。但是,如果有一种装置可以让患者的心脏保持跳动,甚至提高他们的生活质量,将会怎样呢?

有限元法(FEM)vs. 有限体积法(FVM)
有限元法、有限体积法或混合方法:哪一种是 CFD 仿真的最佳选择?这取决于您要求解的流体流动问题。

主题视频:利用 RF 仿真优化测试连接器设计
在射频和微波行业,Signal Microwave 公司一直致力于开发高频同轴连接器,包括终端发射连接器、垂直发射连接器和场转换连接器。在 2018 年波士顿 COMSOL 用户年会上,来自 Signal Microwave 的 Eric Gebhard 讨论了如何使用 COMSOL Multiphysics® 软件为公司带来设计和商业优势。

使用不连续网格模拟共轭传热
在COMSOL Multiphysics®中,您可以在邻近域使用不同的不连续网格。这种能力非常有用,尤其是在模拟共轭传热问题时。
如何将三维结果图导出为可共享的 glTF™ 文件
将 COMSOL Multiphysics® 三维仿真结果制成glTF™ 文件,让您的项目合作人大开眼界!我们将为您展示如何导出绘图,并通过第三方图片查看器进行分享。

如何通过激活材料仿真制造工艺
您需要模拟焊接或增材制造等制造工艺吗?在材料沉积仿真中,您可以利用一项专门的功能来使材料激活或失活。

课程:定义多物理场模型
在 COMSOL® 软件中建立多物理场模型有 3 种方法:全自动、使用预定义耦合的手动和手动使用用户定义的耦合。 在这里,我们讨论第一种方法。

通过光力学模型研究人眼的老花现象
在例行检查过程中,眼科护理专业人员会检查常见的屈光不正症状,如近视、远视和散光。随着患者年龄的增长,医生还会检查老花眼,这是一种眼调节能力减弱的现象,会导致近视力长期完全丧失。视觉调节过程非常复杂,很难获得改进老视诊断和治疗所需的有用眼睛特性。为了解决晶状体折射率的测量问题,研究人员利用仿真开发了一种逆向工程技术。

在 COMSOL® 中对移动载荷和约束进行建模的 3 种方法
了解在 COMSOL Multiphysics® 中模拟移动载荷和约束的 3 种方法:使用变量、插值函数和从 CAD 几何图形导入的路径。

非标准约束和弱贡献的力量
为了以灵活且独立于物理场的方式扩展 COMSOL Multiphysics® 软件的适用性,您可以使用所谓的弱贡献来实现非标准约束。

COMSOL Multiphysics® 5.4 版本简介
COMSOL Multiphysics® 5.4 版本更新了大量功能与特征,并增加了 2 个激动人心的附加产品:“复合材料模块”和 COMSOL Compiler™。

如何在 COMSOL 中实现瞬态方程的弱形式
了解如何使用 COMSOL Multiphysics® 的基于方程的建模功能实现弱形式来求解瞬态问题。

图像去噪以及其他多维变分问题
通过一个有趣的例子,学习如何解决具有多维度、高阶导数和多个未知数的变分问题:在粒状照片中的图像去噪。

实现不等式约束的方法
学习 2 种在变分问题中强制执行不等式约束的方法,即拉格朗日乘子法和增广拉格朗日法,以及它们背后的理论。
