
到目前为止,我们在混合建模系列博客中还没有详细讨论的一件事是,当向我们的计算中增加更多计算资源时,我们可以期待怎样程度的加速。今天,我们考虑一些解释并行计算局限性的理论研究,并将介绍如何使用 COMSOL 软件的批处理扫描 选项。这是一个内置的、易并行计算功能,可在达到极限时提高性能。
Amdahl 定律和 Gustafson-Barsis 定律
我们之前已经提到过的如何通过增加计算单元来提高速度是基于算法的(在这篇文章中我们将使用术语进程,但添加的计算单元也可以是线程 )。一个严格的串行算法,像计算Fibonacci 数列的元素,完全不能从增加过程中受益,而并行算法,如向量加法,可以利用与向量中的元素一样多的处理器。实际中的大多数算法都介于这两者之间。
为了分析一个算法可能的最大加速,我们将假设它由一小部分完全并行化的代码和一小部分严格串行化的代码组成。我们调用并行代码 \varphi 的分数,其中,\varphi 是介于(包括) 0 和 1 之间的一个数字。这自动意味着我们的算法有一个等于 (1-\varphi) 的串行代码片段。
考虑 P 个活动进程的计算时间 T(P),从 P=1 开始,我们可以使用表达式 T(1) = T(1) \cdot(\varphi + (1-\varphi))。当运行 P 个进程时,代码的串行部分不受影响,但完全并行化的代码的计算速度将提高P倍。因此,P 进程的计算时间为 T(P)=T(1) \cdot (\varphi / P + (1 -\varphi)),加速度为 S(P):=T(1)/T(P)=1/(\varphi/P+(1-\varphi))。
Amdahl 定律
这个表达式是Amdahl 定律的核心。对于不同的值 \varphi 和 P 绘制图 S(P) ,我们现在在下图中看到一些有趣的东西。
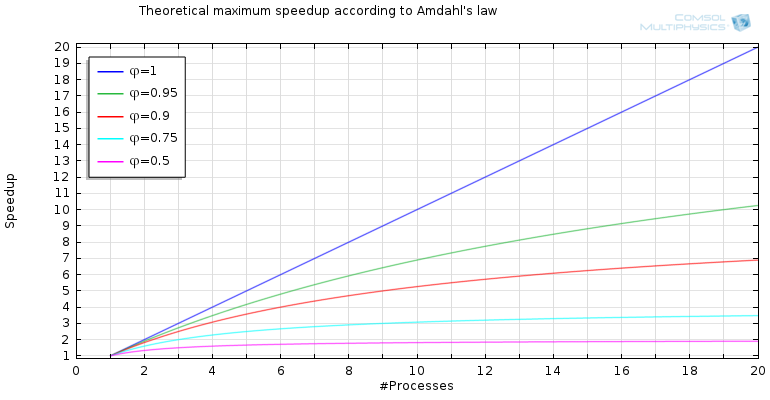
为可并行化代码的不同部分增加进程数的加速比。
对于 100% 并行化代码,极限是不存在的。然而,我们发现对于 \varphi<1,渐近极限或理论最大加速比为 S_{max}(\varphi):=\lim_{P\to \infty} S(P)=1/(1-\varphi)。
对于 95% 并行化的代码,我们发现 S_{max}(0.95)=20,即使我们有无限数量的进程,最大加速也是 20 倍。此外,我们有 S_{max}(0.9)=10, S_{max}(0.75)=4 和 S_{max}(0.5)=2。当减少并行化代码的比例时,理论最大加速比会迅速下降。
但不要现在就放弃回家!
Gustafson-Barsis 定律
Amdahl 定律没有 考虑到一件事,那就是当我们购买一台速度更快、内存更大的计算机来运行更多进程时,通常不是想更快地计算之前的小模型。相反,我们想要计算新的、更大(更酷)的模型。这就是 Gustafson-Barsis 定律的全部内容。它基于这样一个假设,即我们要计算的问题的规模随着可用进程的数量线性增加。
Amdahl 定律假定问题的大小是固定的。当添加新的处理器时,它们处理的是最初由较少数量的进程处理的部分问题。通过添加越来越多的进程,我们并没有充分利用所添加进程的全部能力,因为最终它们能够处理的问题大小达到了下限。然而,假设问题的大小随着添加的进程数量的增加而增加,那么我们就将所有进程利用到假设的水平,并且执行计算的加速是无限的。
描述这种现象的方程是 S(P)=\phi\cdot P-(1-\phi),这为我们提供了一个更为乐观的结果,即所谓的缩放加速(类似于生产力),如下图所示:
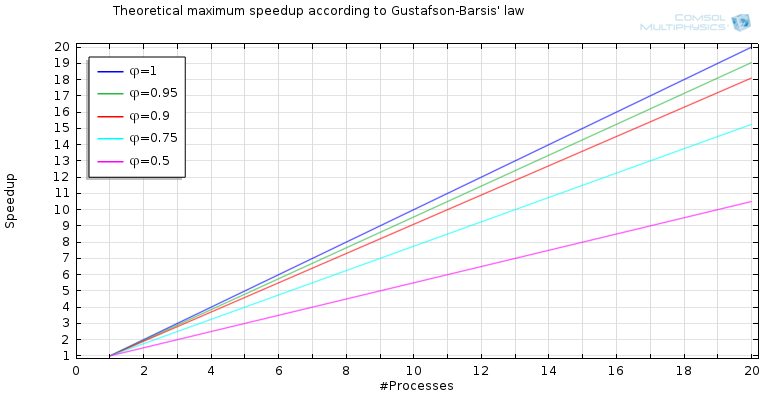
当考虑到工作的规模通常会随着可用进程的数量而增加时,我们的预测就更加乐观了。
通信成本
Gustafson-Barsis 定律意味着,我们拥有的能添加到进程中的资源才能限制我们可以计算的问题的大小。然而,还有其他因素会影响加速。到目前为止,我们在这个系列博客中试图强调的一点是,通信成本较高。但是我们还没有谈到它有多贵,所以让我们看一些例子。
让我们考虑在并行进程中由所需的通信和同步所主导的系统开销,并将其描述为计算时间的增加。这意味着当我们增加进程数量时,通信量也会增加,而这种增加将被函数 OH(P)=c\cdot f(P) 所描述,其中 c 是一个常数,f(P) 是某个函数。因此,我们可以通过以下方式来计算加速比:S(P)_{OH}=1/(\varphi/P+(1-\varphi)+c \cdot f(P))。
下面的图显示了并行化代码的比例为 95% 的情况,我们可以看到对于不同的 f(P) 函数,加速比随着进程数量增加的情况,假设 c=0.005(这个常数在不同的问题和平台之间会有所不同)。在没有系统开销的情况下,结果正如 Amdahl 定律所预测的那样,但是当我们开始增加系统开销的时候,我们看到一些事情正在发生。
对于线性增加的系统开销,我们发现在通信开始抵消更多进程增加的计算能力之前,加速比不会大于 5。对于二次函数,f(P),结果甚至更糟,您可能还记得我们之前关于分布式内存计算的博客文章,在多对多通信的情况下,通信的增加是二次的。
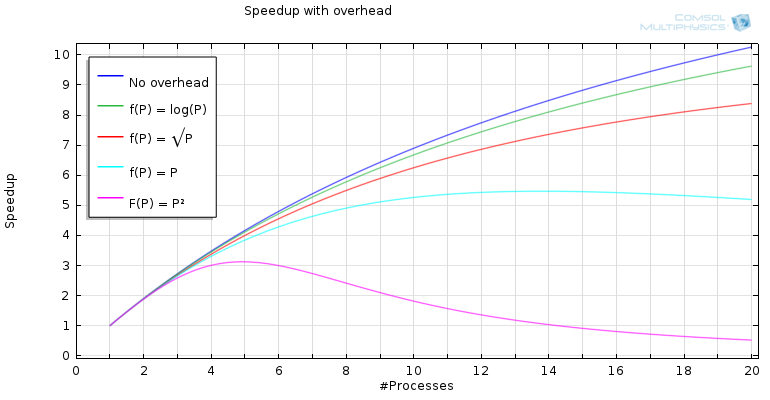
增加系统开销的加速比。常数 c 被选为 0.005。
由于这种现象,当添加越来越多的进程时,我们不能期望在集群上有加速,例如,一个小的瞬态问题。通信量的增加将比增加进程带来的任何增益都快。然而,在这种情况下,我们只考虑了一个固定的问题大小,随着我们增加问题的规模,通过通信引入的“减速”效应将变得不那么重要。
COMSOL Multiphysics 中的批处理扫描
现在让我们离开理论,学习如何使用 COMSOL Multiphysics 中的批处理扫描功能。作为我们的示例模型,我们将使用 COMSOL 模型库中提供的无极灯。该模型很小,大约有 80,000 个自由度,但在其解中需要大约 130 个时间步长。为了使这个瞬态模型参数化,我们将计算不同功率的灯模型,即 50W、60W、70W 和 80W。
在我的工作站,一台配备 Intel®Xeon®E5-2643 四核处理器和 16GB RAM 的富士通 ®CELSIUS® 上,得到了以下计算时间:
| 内核数量 | 每个参数计算时间 | 扫描计算时间 |
|---|---|---|
| 1 | 30 分钟 | 120 分钟 |
| 2 | 21 分钟 | 82 分钟 |
| 3 | 17 分钟 | 68 分钟 |
| 4 | 18 分钟 | 72 分钟 |
这里的加速远非完美——三核仅为 1.7 左右,四核甚至有所降低。这是因为它是一个小模型,每个时间步内每个线程的自由度数较低。
现在,我们将使用批处理扫描功能以另一种方式并行化这个问题:我们将从数据并行 切换到任务并行。我们将为每个参数值创建一个批处理作业,看看这对我们的计算时间有什么影响。为此,我们首先激活“高级研究选项”,然后右键单击“研究1”并选择“批处理扫描”,如下面的动画所示:
如何在模型中激活批处理扫描,包括参数值,并指定同时作业的数量。
下图显示了通过控制并行化可以获得的生产率或“加速比”。当使用4个内核运行一个批处理作业时,我们从上面得到的结果是:72 分钟。当将配置同时更改为两个批处理作业时,每个批处理作业使用 2 个核,我们可以在 48 分钟内计算所有参数。最后,当同时计算4个批处理作业时,每个批处理作业使用一个处理器,总计算时间为 34 分钟。这使速度分别提高了 2.5 倍和 3.5 倍——比单独使用纯共享内存进行并行化要好得多。
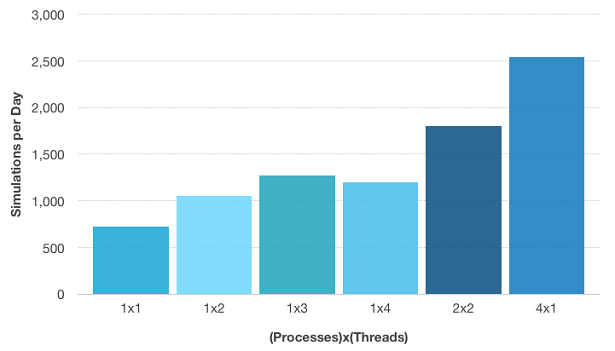
无极灯模型的每天模拟。“4×1”表示 4 个批处理作业同时运行,每个作业使用一个内核。
混合建模系列博客结语
在这个系列博客中,我们了解了共享、分布式和混合内存计算,以及它们的优缺点,以及并行计算的巨大潜力。我们还了解到,在计算领域,没有免费的午餐。我们不能只是添加流程,并希望为所有类型的问题提供完美的加速。
相反,我们需要选择最好的方法来并行化一个问题,以便从硬件中获得最大的性能增益,这就像在解决一个数值问题时,我们必须选择正确的求解器来获得最佳求解时间。
选择正确的并行配置并不总是容易的,而且很难事先知道应该如何“混合”并行计算。但在许多其他情况下,经验来自反复琢磨和测试,然而使用 COMSOL Multiphysics,我们就有可能做到这一点。用不同的配置和不同的模型自己尝试一下,很快您就会知道如何设置软件以获得硬件的最佳性能。
Fujitsu 是 Fujitsu Limited 在美国和其他国家/地区的注册商标。CELSIUS 是 Fujitsu Technology Solutions 在美国和其他国家/地区的注册商标。Intel 和 Xeon 是 Intel 公司在美国和/或其他国家/地区的商标。



评论 (0)