
在这篇博客文章中,我们将研究使用 COMSOL Multiphysics® 软件及其附加的 AC/DC 模块建立的一个 12 槽 10 极永磁(PM)电机模型示例。该示例中的机器是一个具有代表性的旋转装置,外径为 35mm,轴向长度为 80mm。对该模型的输入条件稍加修改,就可以生成一个电动机或发电机模型。在即将发布的系列博客文章中,我们将详细介绍本文中讨论的每个设计。
本文是系列博客的第一篇文章,讨论如何使用 COMSOL Multiphysics® 软件的建模和后处理功能来深入了解旋转机械的一些设计。
电动机和发电机设计:模型设置
在永磁电动机中,来自转子的磁场与由定子电流产生的磁场同步旋转。转子和定子磁场的相互作用产生净转矩,净转矩使电动机能够将绕组的电流转换为机械功率。由于励磁的同步特性,在永磁电动机中瞬时转矩受转子角位置的影响很大,因为该位置与定子电流同步。在异步电机中则是不同的,在异步电机中,定子绕组感应出的转子磁场是转子和定子之间的速度滞后的函数(因此俗称感应电机)。
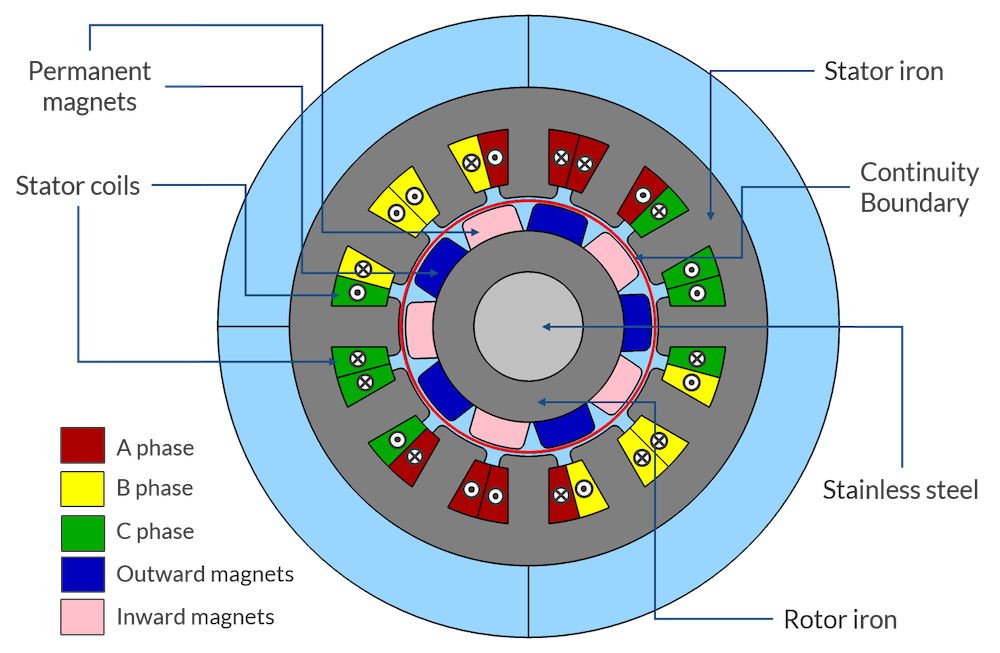
永磁电机模型示意图。
线圈励磁将具有以下形式: I = I_m cos(\kappa \alpha + \phi), 其中,I_m 是峰值电流,\kappa 是取决于极数的比例因子,\alpha 是转子角,\phi 是相位角。在此示例中,三相的激励分别由下式给出:I_a = I_m cos(\kappa \alpha), I_b = I_m cos(\kappa \alpha – {120}^{\circ}), 和 I_c = I_m cos(\kappa \alpha – {240}^{\circ})。
为了确保定子和转子磁极之间的吸引力和斥力产生单向转矩,比例系数必须是这样的:当转子以一个转子磁体的角度跨度移动时(磁体具有交替的极性),定子线圈的磁场是反向的。其值由下式给出 \kappa = \frac{{180}^{\circ}}{{360}^{\circ}/N_p},其中,N_p 是转子极数,分母给出了单个转子磁极的角跨度。
研究和优化磁场分布
磁场分布 是电机设计中非常重要的因素。在同步旋转电机中,研究感应电压的关键参数是气隙磁通(即转子和定子之间交换的磁通)的空间分布。仅当径向磁通沿转子外围具有正弦分布时,定子相电压才为正弦。该空间波形也称为气隙磁动势(MMF)波。如果磁动势波不是正弦波,那么在感应电压中会引入高次谐波。
在这个模型中,为了获得气隙磁动势波,我们评估了沿连续性边界的磁通密度的径向分量。随着转子旋转,我们可以观察到磁动势波如何随时间演化。仅仅通过观查,我们就可以了解到感应电压不会是完美的正弦波。在即将发布的博客系列中,我们将说明如何获得气隙磁动量的时空傅立叶变换,以及如何将其与串联磁通和电压的谐波失真相关联。
左:磁通密度随转子旋转而变化。右:随着转子旋转,气隙磁动势波的传播。
研究和优化机械转矩
对于永磁电动机的特定槽/极组合,有多种激励定子绕组的方法。永磁电机模型示意图中显示的模式(这篇博客文章中的第一个图)是可以驱动 12 槽 10 极永磁电动机的一种方法。我们需要调整定子线圈的励磁(或初始转子位置),以便将最大扭矩施加到转子上。为此,我们给转子一个初始角位移。转子角度 \alpha 在一个转子磁铁的角度跨度上变化,并会计算出平均转矩。选择与最大平均转矩相对应的初始角位移值作为转子的初始位置。按照这种方式,定子和转子的相对位置产生最大转矩将变得更容易可视化。
在下列情况下,可以观察到两个最大值:
- 电动模式运行时对应的正最大值,即,将电能转化为机械能。
- 发电模式运行时对应的负最大值,即,将机械能转换为电能。
下一节中给出的转子转矩波形对应于平均转子转矩曲线的正最大值。在即将发布的博客文章中,我们将更加深入地研究扭矩检查和扭矩计算的各种方法,例如 Arkkio 方法 和虚功原理。
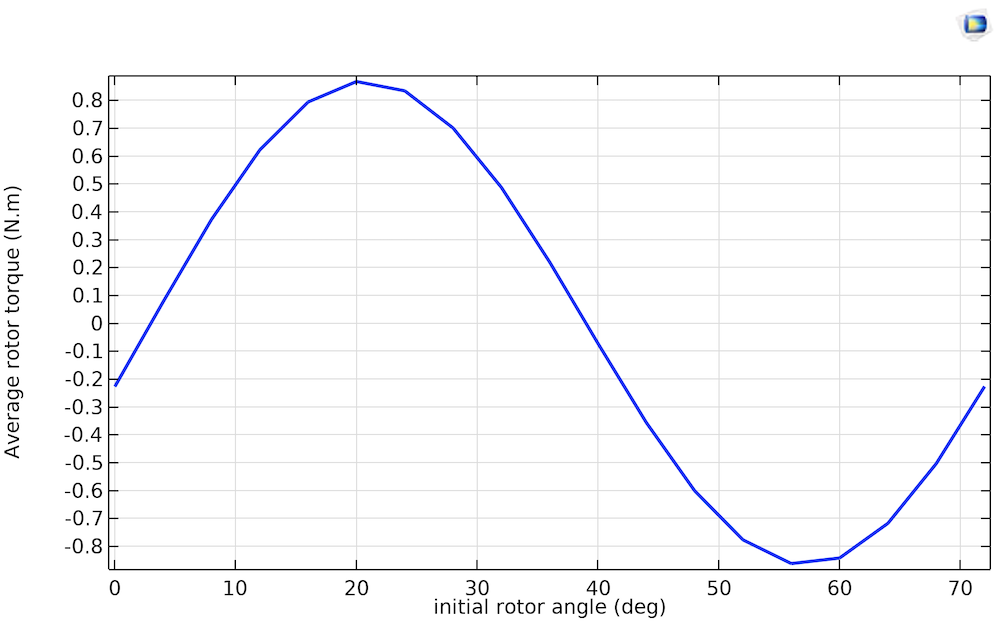
在两个转子磁极范围内,平均转子转矩随初始转子角(2 \times \frac{{360}^{\circ}}{N_p} = {72}^{\circ})的变化。
调查和优化铁用量和损耗
通过使用磁通密度图,我们可以研究铁芯中的磁通密度分布。在模型几何的某些部分,磁轭可能会形成瓶颈区域,并可能会将磁通量密度值推入B-H曲线的饱和区域。在另一些情况下,它的宽度足以引起低场强区域。当磁轭的某个部分始终显示出弱磁场时,这部分就未充分利用来产生扭矩。当某个部分形成一致的瓶颈时,这部分可能应该扩大。
在该示例中,转子和定子中铁的厚度发生了改变,我们检查了其对转子转矩的影响。为了产生最大扭矩,初始转子角设置为 {20}^{\circ},这是从上一节中的平均扭矩曲线获得的。从下面的曲线图和扭矩曲线中可以看出,当铁的厚度约为 2mm 时,铁的利用率最佳:小于 2mm 会对扭矩产生负面影响,而大于 2mm 则会增加不必要的材料—从而增加重量和成本。
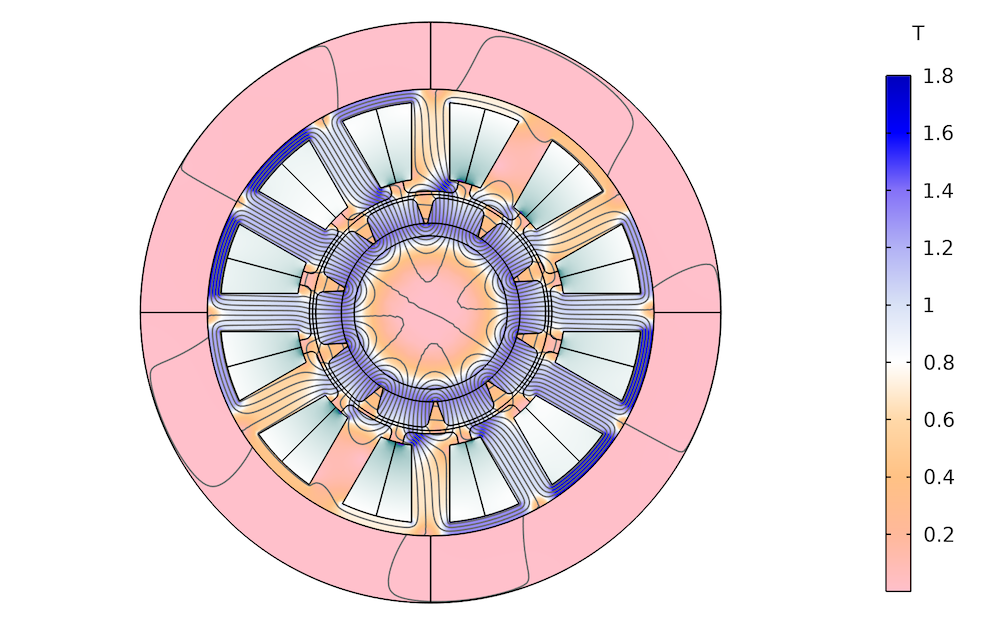
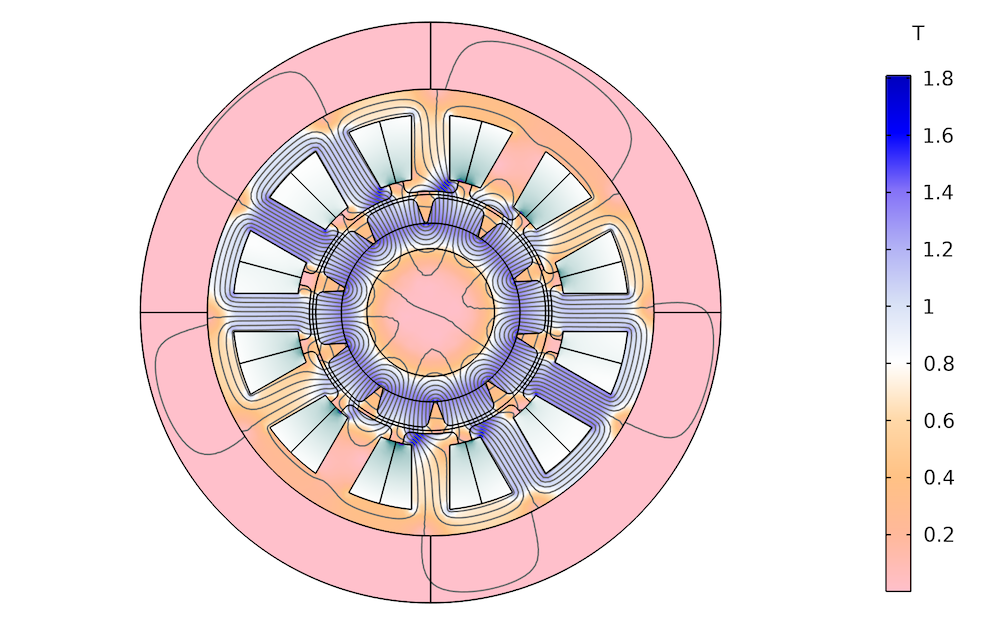
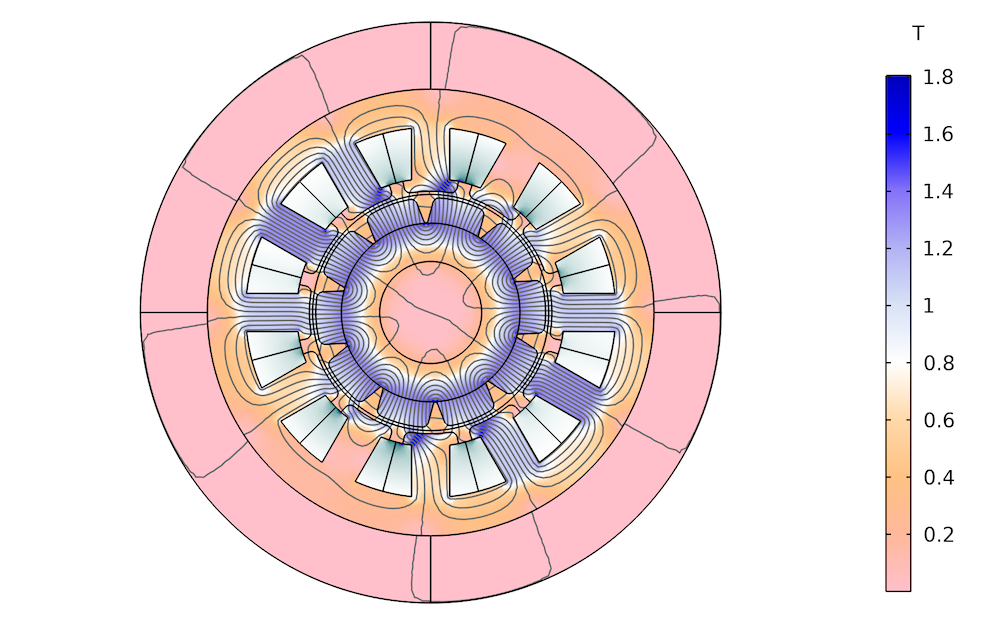
不同厚度铁的磁通密度分布。左:1mm。中心:2mm。右:3mm。
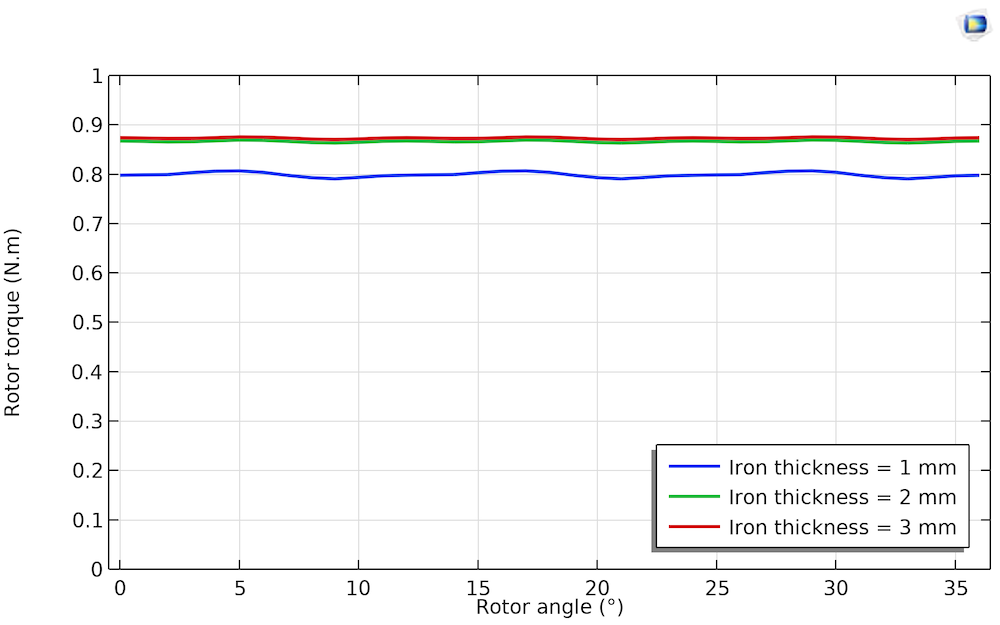
随铁厚度变化的转子转矩波。
但是,这还不是全部内容:确定铁的厚度时还需要考虑其他因素,例如机械强度以及电阻和磁损耗。在研究磁通密度和转矩时,也可以评估铁厚度变化对铁损耗的影响。从 COMSOL Multiphysics 5.6 版本开始,软件内置了损耗计算 特征,可使用 Steinmetz 方程、Bertotti 公式或用户定义的损耗模型轻松评估铜损耗和铁损耗。在即将发布的博客文章中,我们将进一步讨论旋转机械的多物理场建模,例如效率计算、温升评估、振动分析和噪声检查。
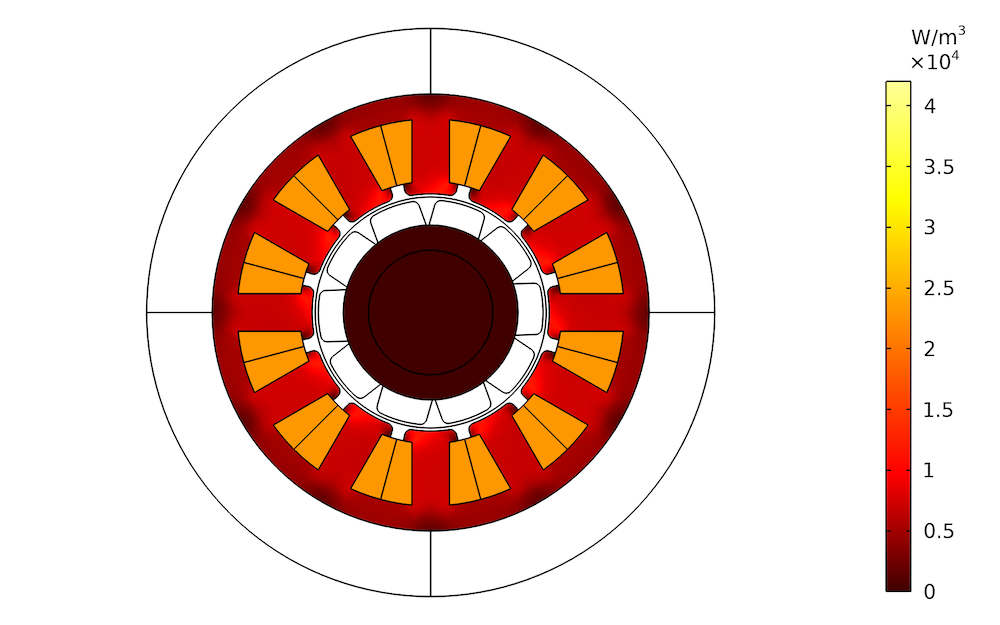
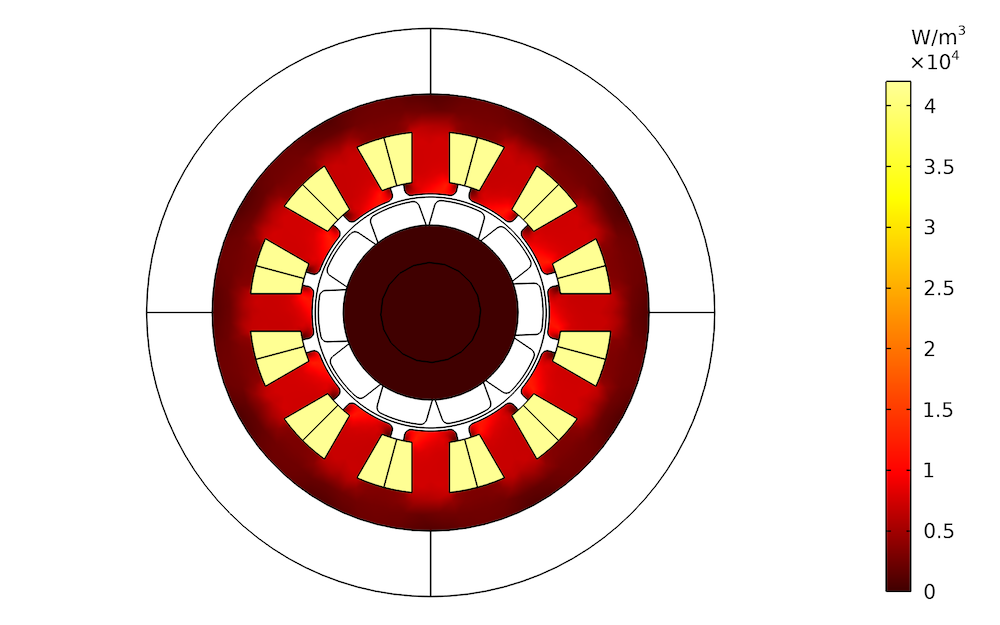
不同铁厚度值的铁损分布。左:1mm。中心:2mm。右:3mm。
总结
在这篇文章中,我们讨论了 COMSOL Multiphysics 和 AC/DC 模块中一些功能的使用,轻松了解了旋转电机的一些设计。我们可以通过气隙中径向磁通密度的线图了解到感应电压是否为正弦波;可以使用 COMSOL Multiphysics 中的 参数扫描 功能 确定将产生最大转子转矩的初始转子角;可以通过机械磁通密度的表面图直观地确定铁的利用率是否对于有效产生扭矩而言是最佳的。使用 COMSOL Multiphysics 提供的内置损耗模型,也可以观察铁厚度对铁损耗的影响。
在这个系列博客的第一篇文章中,我们讲解了如何使用 COMSOL Multiphysics 强大的建模和后处理功能获得对旋转机械设计的一些宝贵的见解。随后的博客文章将广泛讨论转矩计算方法、效率计算、铁损耗和热性能分析,以及电机振动和噪声检查。敬请关注!
自己尝试
单击下面的按钮,尝试自己对文中讨论的电动机进行建模:







评论 (4)
磊 赵
2024-06-13你好,请问这个模型在哪里下载?链接里没有MPH模型
hao huang
2024-06-14 COMSOL 员工您好
目前该案例在修复中,暂时下架。
如果有进一步问题,建议您联系 COMSOL 的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
Xin LI
2024-09-11你好,请问该案例修复好了吗,什么时候可以下载呢
hao huang
2024-09-11 COMSOL 员工您好
目前该案例还在修复中,如果有相关问题可联系技术支持。
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!