
在最近的后处理系列博客中,我们演示了流体、力学、化工及电气应用中常用的几种绘图类型。在本系列接下来的几篇博客中,我们会介绍一些不太常用的、仅针对特定应用的绘图类型,还将介绍其他一些您可以用于改进图形化显示的工具。本篇博客中,我们将重点介绍极坐标图、远场图和粒子追踪图。
极坐标图
极坐标图正是您在数学课上学过的那种绘图。它们会使用极坐标分量 r 和 $\theta$ 来描述诸如声场或电磁场等的模式。这些绘图可以帮助您获取有关器件辐射模式的局部绘图或俯视图。例如,您可以通过极坐标图来分析声波如何从扬声器中传出及其传播范围,以便验证扬声器的设计是否满足声音分布最为均匀的优化。
我将通过锥形天线模型的极坐标图来演示这一点。(如果您已经安装了 RF 模块,可以点击文件 > App 库 > RF 模块 > 天线访问该仿真模型。)模型分析了锥形天线的阻抗及辐射模式。下图显示了天线的几何结构:

天线将同轴电缆中沿 z 方向传播的电磁波辐射出去,模型结果显示了不同频率下天线附近的辐射模式。下方的极坐标图绘制了随仰角$\theta$改变的近场辐射模式。
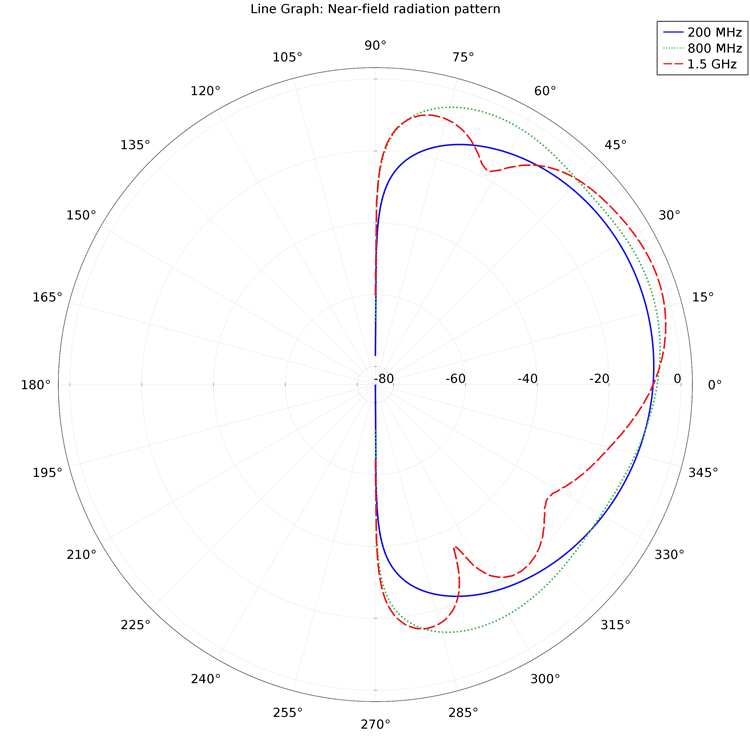
远场图
与极坐标图不同,远场图主要绘制远离源处的波型(电磁波或声波)。例如,锥形天线的远场图如下所示:
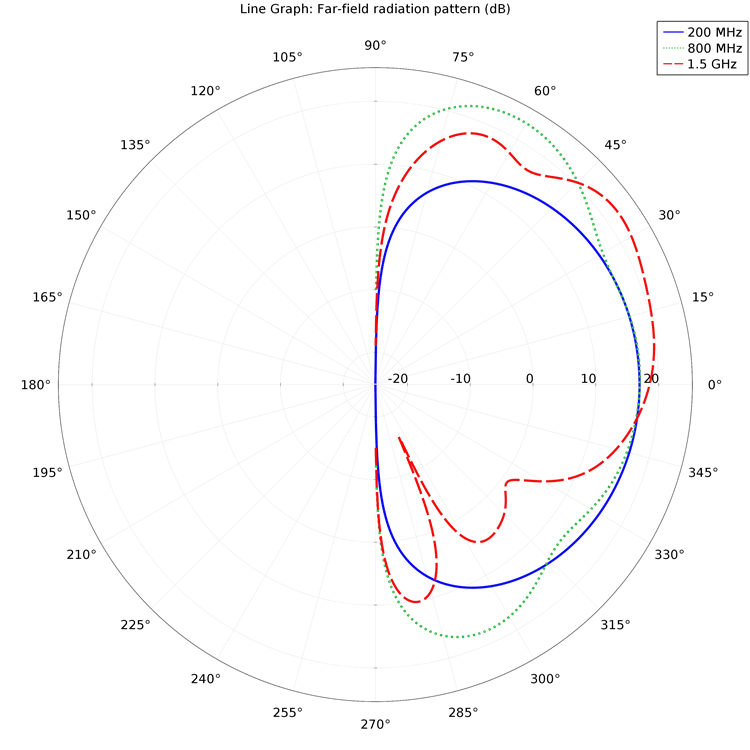
对比远场图与之前的近场图,可以看到辐射模式在距离天线很远处发生很大改变。
不过远场图通常会在三维下显示,因此并非局限于极坐标图。可以绘制圆(2D)或者球(3D)上指定角范围内的变量分布图,同时可以指定角间隔及圆或球的起点及半径。通过改变辐射方向上球或者圆的半径可以得到远场辐射图,也就是说球或者圆的半径恰好等于该点上表达式的值。(这一绘图类型的一个优点是,用来定义绘图方向的圆或球并非模型几何的一部分,所以绘制方向的数量与求解域无关。)
下方重点显示了锥形天线的三维远场图。您将注意到,图中清楚地绘制出了波型,相对极坐标图中的局部数据,它给出了一个更具“整体观”的绘图。
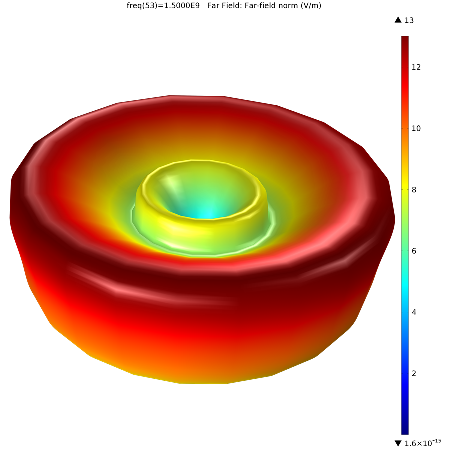
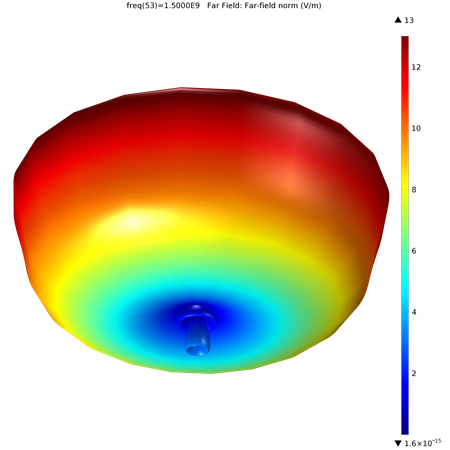
粒子追踪图
最后,我们将再介绍一下 COMSOL 中专门针对粒子追踪应用的几个绘图类型:粒子追踪图、庞加莱图和相图。我将使用层流混合器模型来演示这些绘图类型。如果您安装了粒子追踪模块,就可以在文件 > App 库 > 粒子追踪 > 流体流动 下找到该模型。
仿真分析了被泵入含固定叶片管道中的流体。这种混合技术特别适用于层流混合,因为其中的压力损耗很小。模型通过追踪悬浮在混合器中的粒子轨迹评估了混合效果。
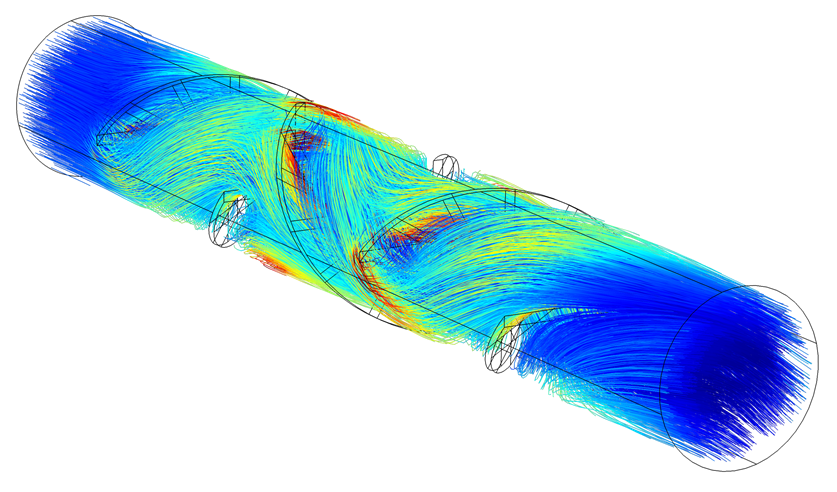
粒子追踪图绘制了指定数量、密度或直径的粒子的实际轨迹。在本模型中,将一种物质溶于室温下的水。然后将粒子释放到混合器中,5 秒钟后,针对每个粒子设置一条线进行追踪,下图显示了追踪结果。颜色表达式基于流动的剪切速率 (1/s)。
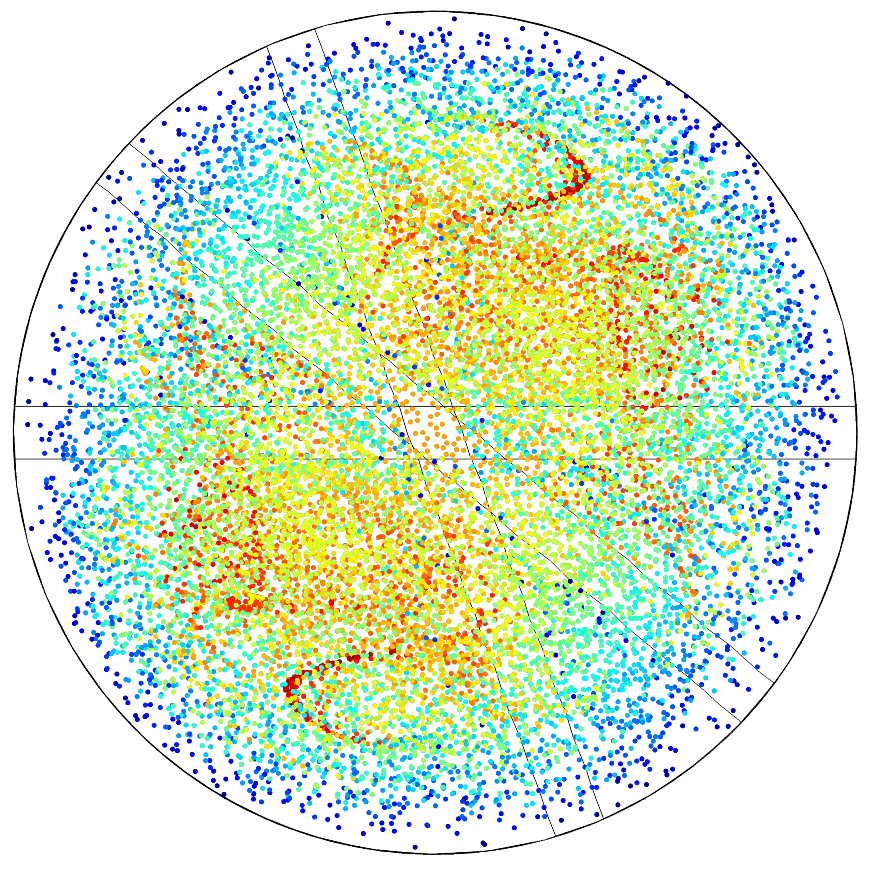
庞加莱图是模型中包含的另一类三维绘图组,也是第一类循环映射。这些二维绘图通过定义在粒子数据集上的一个截面创建,显示了粒子在位于轨迹截面上的位置。庞加莱图在低于原始粒子空间维度一个维度的空间维度上表征了粒子轨迹。绘图显示了粒子穿过截平面的位置点,如果同一个粒子多次穿过平面,则会包含多个位置点。在下方的绘图中,点的颜色说明了经释放 5 秒钟后,粒子穿过平面的速度。
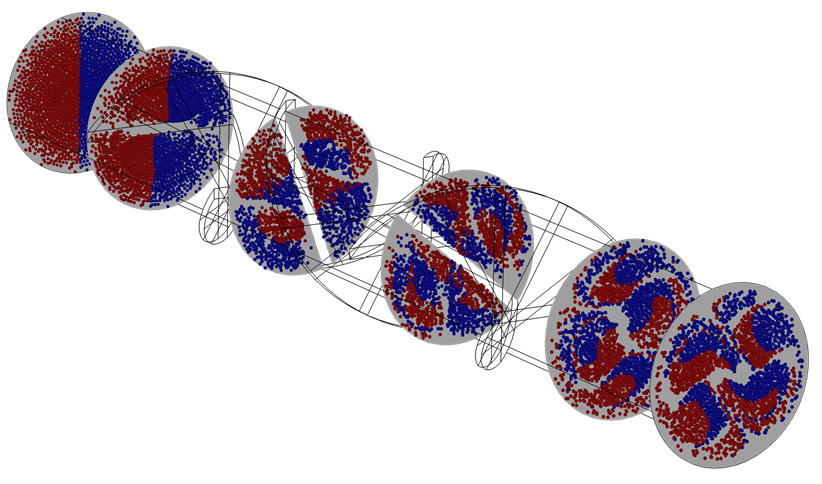
庞加莱图的一个使用技巧是在一个三维绘图组中加入多个庞加莱图。例如,下方的结果图绘制了混合器不同位置处的庞加莱图,同时绘出了下方叶片的廓线。此时,点图的颜色说明了溶解水平(物质在水中的混合情况):
我们将讨论的最后一个绘图类型是相图。同庞加莱映射类似,相图在二维绘图中显示粒子的位置。但是,截面并非一定位于粒子传播方向的截线上。相图常用于同时绘制粒子位置与速度,位置将取决于距起点的距离。下方的相图绘制了 t = 5s 时的粒子位置:

以上就是我们基于具体应用的绘图类型。希望您喜欢本期的介绍,并从中学到一些可用于 RF、声学及粒子追踪仿真的结果显示及数据收集方法。敬请期待我们稍后将发布的有关如何在结果图中使用变形的博客!



评论 (0)