
今天的特约作者,是来自 COMSOL 认证咨询机构 — Boffin Solutions 有限责任公司的 Ionut Prodan,他将会和我们一起讨论运用混合方法计算薄层结构中的裂隙流动建模。
当在三维多孔基体中对薄层裂隙进行建模时,您可以通过裂隙流接口将它们模拟为二维对象,以有效地描述其压力场。然而,很多时候,我们对裂隙通量的计算更感兴趣,例如非常规储层中的水力压裂。让我们来看看混合方法是如何攻克这些难题的。
从三维到二维:薄层裂隙建模
为了运用“地下水流模块”建立真实裂隙的二维对象模型。首先,需要求解位于内表面的压力场(通过 Darcy 定律的切向形式),以表征裂隙沿切向的伸展。然后将速度场沿某一边界的法向分量和裂隙厚度相乘(确定二维裂隙对象边界),便可计算通过实际裂隙横截面的流体通量。这种方法具有更高的计算效率,我们只需要将它绘制成表面网格,就可以将超薄但足够宽的三维对象简化描述为二维对象。
您创建的二维裂隙模型应具有以下特征:
- 具有一条位于多孔基体内部的边缘。
- 该区域比周围结构具有更高的渗透性。
- 其侧面和横截面具有较大长宽比。
在这样一个系统中,裂隙通量的计算往往会发生误差。让我们看看下面这个例子。
注意:借助 COMSOL Multiphysics® 软件最新的 — version 5.2a 版本,您也可以对薄层裂隙中的传热进行建模,这是通过裂隙传热接口实现的。
解决裂隙通量计算误差:以储层块为例
在下图所示的系统中,一条三维硬币形压裂裂缝包含在储层中,并与水平井相连。这个简化系统的入口由两个位于贮槽块顶部和背部的贮槽边界(图中绿色部分)组成。唯一的出口位于裂隙盘与井筒相连接的狭窄边界处。入口和出口都设置为压力边界条件,值分别为 ΔP 和 0。因其具有对称性,所有只需对实际系统几何形状的四分之一部分进行考虑。
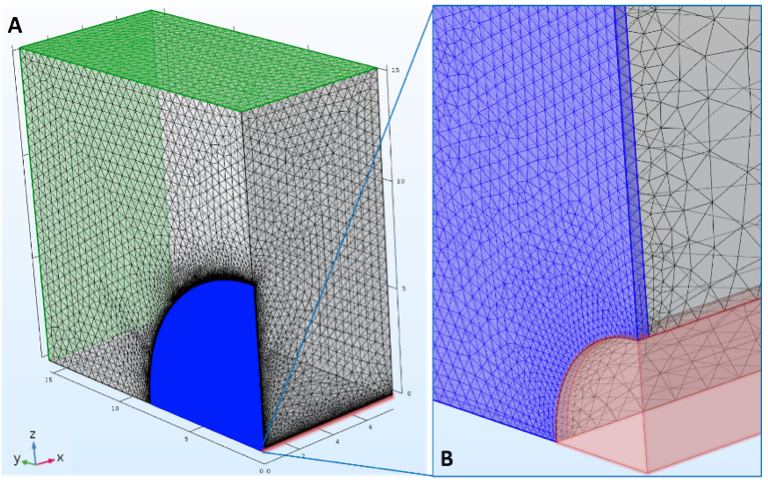
一条三维硬币形裂隙(图中蓝色部分)被嵌入储层中,并与水平井(图中红色部分)液压连接。两个储层入口边界用绿色突出显示。
请注意,上述系统的尺寸不代表实际尺寸。我们将尺寸按比例缩小了,以便提供充足的盘状裂隙进行三维网格剖分,缩小后的半径为 7.62 米(25 英尺),厚度 d_{HF} 为 1.27 厘米。(如果按照实际应用中那样,以百英尺数量级的半径来精确绘制三维裂隙网格剖分,这会使计算成本过高。)井筒半径为 12.7 厘米(5 英寸),而贮槽块的尺寸约为 8 米 × 15 米 × 15 米(25 英尺 × 50 英尺 × 50 英尺)。 整个网格由 2,246,298 个四面体单元组成,其中 657,720 个仅用于盘状裂隙区域。后者的最小单元质量及平均单元质量值分别为 0.148 和 0.700,而整个网格的平均质量为 0.673。
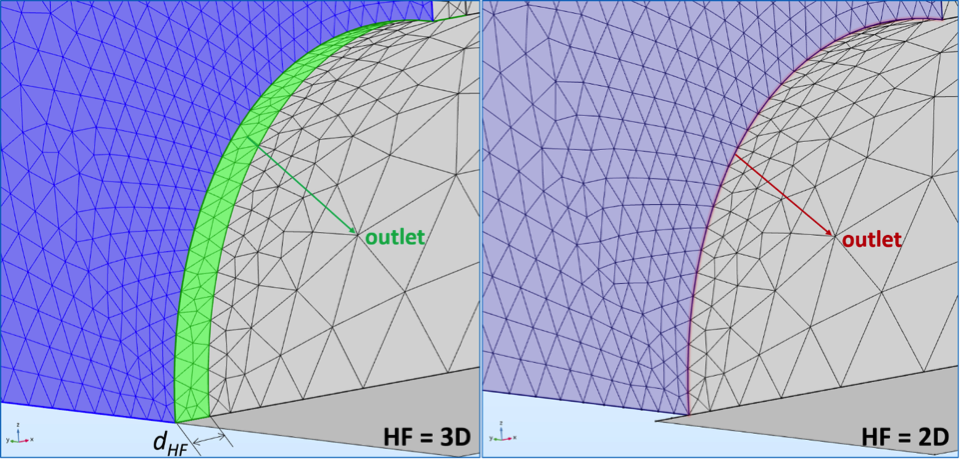
真实水力压裂中厚度为 dHF 的出口边界的三维(图中绿色部分)及二维(图中红色部分)表示方法。
在不可压缩、单相、定常流动参数的情况下对不同水位降低 ΔP 取值进行研究时,可用 Darcy 定律 {\overrightarrow{u}}=-\frac{K}{\mu} \nabla p 求解压力场 。该液体是一种轻质液态烃,其动力粘度值 \mu 为 0.26 cP。贮槽基体的渗透率为 1 mD,水力压裂的渗透率为 45.6 Darcy。
上文所述的裂隙通量计算问题如下图所示。当水力压裂(HF)被描述为三维或二维对象时,图中显示的入口和出口流速为水位降低 ΔP 的函数。如预期一样,前三条曲线(入口流速曲线和三维出口流速曲线)重叠,二维表示法下的出口流速只代表入口流速的四分之一。前三条曲线的通量通过流体速度矢量 {\overrightarrow{u}} 在入口和出口表面法向分量的积分进行计算 (\smallint\smallint {\overrightarrow{u}} \cdot {\hat{n}} ̂dA〗) 。同时,二维裂隙的出口流速描述为沿出口边缘的的积分 {\overrightarrow{u}} \cdot {\hat{n}} ,并与裂隙厚度 dHF 相乘:
Q_{Out}^{2D}=d_{HF} \smallint {\overrightarrow{u}} \cdot {\hat{n}} ̂dl〗 。
无论运用哪种网格剖分,以及无论以何种方式探测 Q_{Out}^{2D}, 都会存在 \smallint {\overrightarrow{u}} \cdot {\hat{n}} ̂dl〗 通量计算问题,其被积函数表达式为:(dl.nx*dl.u + dl.ny*dl.v + dl.nz*dl.w),(sys1.e_n1*dl.u + sys1.e_n2*dl.v + sys1.e_n3*dl.w),dl.bndflux/dl.rho,或者为 (root.nx*dl.u + root.ny*dl.v + root.nz*dl.w)。“dl.”标识符代表应用接口(Darcy 定律接口);{nx,ny,nz} 指垂直于边缘 的法向矢量的笛卡尔坐标分量 {\hat{n}}〗;{u,v,w} 指流体速度矢量 {\overrightarrow{u}} 的笛卡尔坐标分量。
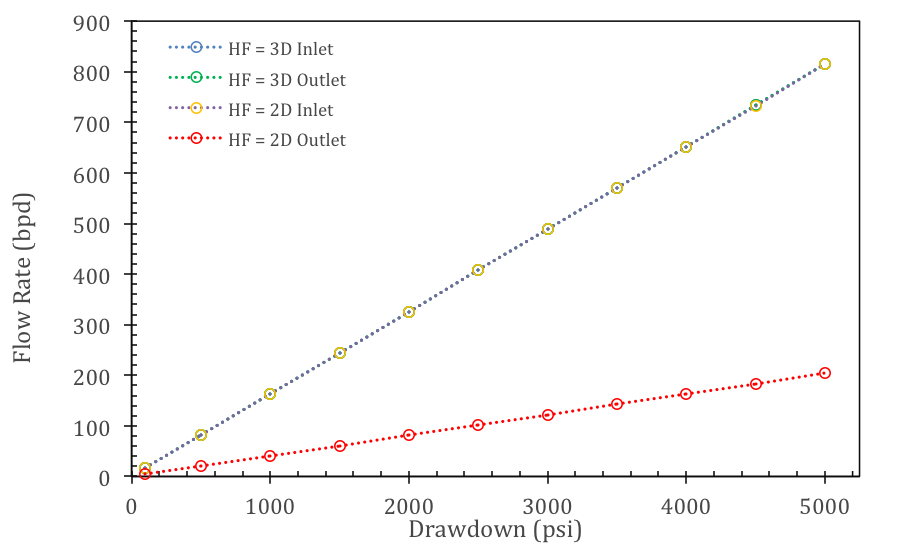
当真实的 HF 被模拟为各个系统中三维或二维对象时,入口和出口流速为水位降低 ΔP 的函数。
请注意,当水力压裂被描述为二维对象时,盘状裂隙(三维)域从模型中被省略,只有当其通过内部侧边界时才会被考虑。另一方面,二维和三维描述中的几何和网格是相同的。这种简化大大缩小了系统的尺寸,这也正是裂隙水流接口中的对用户最具吸引力的单元:它使通过适当的网格剖分对大尺寸裂隙表面的建模成为可能。因此,如果有一种方法可以避免二维裂隙出口通量问题时,它将非常实用。
借助混合方法解决裂隙通量守恒问题
混合方法可以将远离井筒的裂隙的二维描述和其附近裂隙的三维描述相结合。下图显示了由混合方法实现的网格剖分几何。蓝色区域代表裂隙的三维分量;红色表面代表裂隙的二维分量,描述了向多孔基体延伸的实际裂隙流边界。请注意,与二维分量相对应的实际裂隙的三维部分并未包含在模型中。

混合方法实现的网格剖分几何图形。蓝色区域代表裂隙的三维分量,红色表面代表裂隙的二维分量。后者为真实裂隙的内部侧边界(朝向基体)。
在混合方法中,真实裂隙中任一点的压力场仍旧可以被精确地求解,同时可以在避免二维描述缺点的前提下计算出通过出口边界的通量。下表对三维、二维、混合方法下水力压裂的相关计算量进行了比较。这些计算是通过配备有 Intel® Core™ i74770 处理器和 32 GB 内存的计算机使用直接求解器实现的。
| 水力压裂 | 自由度 | 内存 (GB) | 时间迭代 (s) | Q_{in}/Q_{in}^{3D} | Q_{out}/Q_{in}^{3D} |
|---|---|---|---|---|---|
| 三维 | 3,231,747 | 23.74 | 247.5 | 1 | 1.00026 |
| 二维 | 2,354,490 | 15.98 | 153.5 | 0.99948 | 0.24992 |
| 混合方法 | 2,397,891 | 16.50 | 158.0 | 0.99941 | 0.99967 |
二维及混合方法下相关计算量的比较。
下方的对数刻度绘图显示了沿 YZ-平面(包含二维裂隙表面)内的对角线延伸的压力剖面图,其水位降低为 100 psi。该探测线由位于表面右下部的出口(井筒)及另一端的贮槽块的入口来进行界定。图中插入的白线突出显示了探测线。插图中表面的颜色与 YZ-平面内探测的压力值相对应,图中的导向箭头对重要的参数点起指向作用。在所有三种情况下,图中的曲线都会重叠,表明三维、二维、混合方法这三种描述中的压力场解决方法几乎完全相同。
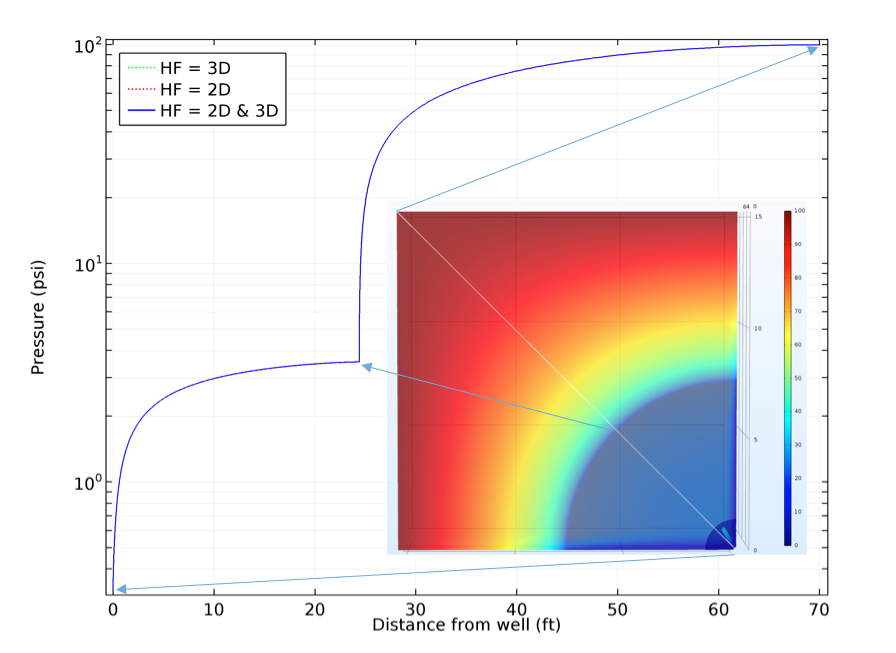
沿 YZ-平面内的面对角线延伸的压力剖面图。
混合方法使薄层裂隙建模更方便
仅对裂隙进行二维描述可能会出现通量计算问题。正如前文所述,我们提出了一种用于描述真实裂隙的混合方法,这是一种可行的解决方案。因此,这种技术可被运用于多种带有大量无规则薄层裂隙的真实系统。
关于特约作者

Ionut Prodan 是 COMSOL 认证咨询机构——Boffin Solutions 有限责任公司的负责人。在创办 Boffin Solutions 之前,Ionut 曾供职于壳牌(Shell)及马拉松石油公司(Marathon Oil)的高端技术部门。他从莱斯大学(Rice University)获得了物理学博士学位,攻读期间他从事超冷原子光缔合和计算固体化学的研究。
Intel 及 Intel Core 为 Intel Corporation 或其位于美国和/或其他国家子公司的注册商标。






评论 (6)
巍 韩
2018-01-28写的很好,请问该案例是否可以分享?谢谢!
宇航 秦
2018-01-29韩巍,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
玉龙 程
2018-10-06你好,请问一下可以分享一下您的模型吗
王 刚
2018-10-19 COMSOL 员工地下水流案例库中有典型示例,可供参考:discrete fracture。可以从以下链接下载:http://cn.comsol.com/model/discrete-fracture-691
Shine Sun
2025-05-26我看了案例库里的这个文件,他用的是插件库中随机生成离散三维裂隙网络的插件,之后进行建模,请问comsol是已经将这种混合计算的方法集成到这个插件库里去了还是在计算过程中自动适配的呢
Haoze Wang
2025-06-09 COMSOL 员工您好,此博客中所提到的混合法,是在井筒附近使用了三维裂隙、远离井筒区域使用了二维裂隙的混合求解方式,目前暂无相关案例。案例库中的模型没有涉及到井筒区域,因此直接使用了裂隙流条件对裂隙进行二维建模和求解。