由 Chien Liu 创作的所有博客

如何模拟半导体器件中的载流子动力学
通过 2 个示例了解如何模拟半导体器件中的载流子动力学:反向恢复和正向恢复 PIN 整流器模型。

如何模拟金属-硅-氧化物电容器的界面陷阱效应
想要分析 MOSCAP 中的界面捕获效果吗?了解如何使用半导体模块中的功能,使您能够向模型添加充电和载波捕获/释放效果。

模拟渐变异质结中的隧穿电流
对半导体设计感兴趣吗?了解量子隧穿效应背后的理论,并通过演示学习如何模拟渐变异质结中的量子隧穿电流。

纳米线基准模型的自洽薛定谔-泊松结果
使用砷化镓纳米线的基准模型验证了“薛定谔-泊松方程”多物理场接口,此接口适用于模拟包含载流子的量子约束系统。
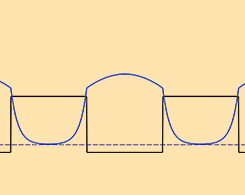
使用薛定谔方程计算超晶格的带隙
在最新版本的 COMSOL® 软件中,您可以在半导体模块中使用新的薛定谔方程 接口进行建模。今天这篇博文,让我们来看一个简单的示例模型,这个模型使用了此接口来估计超晶格结构的电子和空穴基态能级。通过构建类似的模型,器件工程师能够计算给定周期结构的带隙并调整设计参数,直到达到所需的带隙值。 编者注:此博文于 2020 年 1 月 23 日更新,反映了软件最新的功能和信息。 超晶格结构的有效带隙 由于量子限制效应,超晶格结构的有效带隙比体阱材料中的有效带隙更宽——电子和空穴大多被限制在阱中,其基态能量从带边缘偏移。下面显示了一个示例,其中黑色和灰色线表示导带和价带边缘,蓝色和绿色曲线分别表示电子和空穴波函数被基态能量偏移。 超晶格带隙模型的汇总图。 COMSOL Multiphysics® 模型 这个模型简单明了,易于理解。使用了两个 薛定谔方程 接口:一个用于电子,另一个用于空穴。在每个接口下,两个 电子势能 节点用于设置方波形带边缘,同样,两个 有效质量 节点用于设置阱区和势垒区的有效质量。模型中只需要包含一个超晶格结构的晶胞,端点应用 周期性条件 边界条件。 COMSOL 模型开发器树结构。 在两个特征值研究中分别求解电子和空穴的基态能量。使用 数组 一维数据集将结果从一个晶胞扩展到三个晶胞 ,这也是 COMSOL Multiphysics® 软件的新增功能。 关于 薛定谔方程 接口 在物理场接口的设置面板中有一些参数值得注意。 薛定谔方程接口的设置面板。 特征值尺度 一个重要的参数是特征值尺度 λscale (单位: J)。这个参数用于特征值研究,将无单位的特征值相对于特征能量进行缩放。例如,默认值 1eV 允许特征值的数值以 eV 为单位呈现特征能量的值。因此,1.924 的特征值(如下面的屏幕截图所示)对应于 1.924eV 的特征能量。 特征值研究的设置。 如果将特征值比例设置为 1meV,那么相同的特征值将对应于 1.924 meV 的特征能量(来自不同模型的结果)。 能量 另一个参数是能量E(单位:J),用于稳态研究以指定稳态薛定谔方程的总能量。 薛定谔方程接口中的符号约定 时谐因子 在物理场接口中执行的单分量薛定谔方程如下: -\hbar^2 \nabla \cdot \left(\frac{\nabla \Psi(\mathbf {r},t)}{2\, m_{eff}(\mathbf{r})}\right) + V(\mathbf{r},t)\Psi(\mathbf{r},t) = -i \hbar \frac{\partial}{\partial t}\Psi(\mathbf{r},t) 请注意,方程右侧的能量算子采用了与大多数量子力学教科书采用的符号相反的约定。这是因为 COMSOL Multiphysics 对时谐解采用了exp(+iωt) 的工程惯例来约定 ,而不是 exp(–iωt) 的物理学约定。薛定谔方程 接口采用工程约定,因此 COMSOL® 系列产品中的符号约定保持一致。在这种不寻常的符号约定下,动量算子也获得了相反的符号——因为平面波现在是 exp(–ikx + iωt),而不是 exp(+ikx – […]

如何求解两点间的最速降线
两点之间的最短路线不一定是直线。如果将用时最短作为从 A 点到达 B 点的最短路线评判标准,那么在重力作用下,高度不同的两点间的最短路线就是最速降线。在本篇博客文章中,我们将演示如何使用 COMSOL Multiphysics 的内置数学表达式和“优化模块”来求解最速降线。

如何用弱形式实现点源
了解如何在 COMSOL® 软件中用弱形式实现点源。讨论弱式公式的博客系列的第二部分。

借助 COMSOL® 仿真 App 执行弱形式
在之前的弱形式系列博客中,我们对弱形式方程进行了离散,希望得到可用于求解我们简单示例问题中未知系数的矩阵方程。按照博客“在 COMSOL Multiphysics 中执行弱形式”中的步骤操作,我们将能在 COMSOL Multiphysics® 软件中执行该方程,并能加入其他步骤来检查矩阵。我们还发现可以借助 COMSOL® App 更轻松地实现所有相关矩阵的同时展示,并能在同一个屏幕上按类排列。



