由 Walter Frei 创作的所有博客
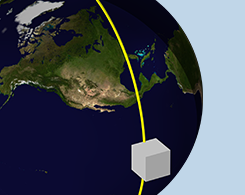
使用 COMSOL Multiphysics® 计算轨道热载荷
2022年 11月 23日
从 6.1 版本开始,传热模块包括一个新的接口,用于定义卫星轨道和方向、轨道机动和变化的行星特性。
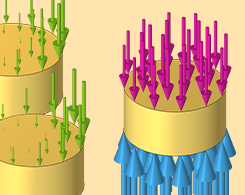
三相输电线路中的损耗
2022年 7月 26日
探索如何模拟以线性和等边排列的三根铜导线中的损耗。

求解大型 COMSOL 模型需要多少内存?
2022年 5月 6日
是否想过您可以在 COMSOL Multiphysics® 中求解多大的模型?这取决于内存需求、模型大小和有限元问题的尺寸。

在 COMSOL® 中计算和可视化卫星轨道
2022年 3月 9日
在这里,我们将介绍一个新的、来自世界各地的轨道航天器教程模型。
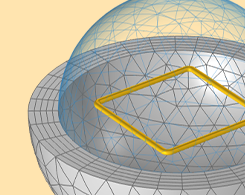
使用 COMSOL® 计算和使用部分电感
2022年 3月 3日
COMSOL Multiphysics®6.0 版带来了计算总电感、部分电感和交流电阻的新功能。
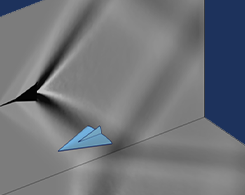
在 COMSOL Multiphysics® 中创建纹影图像
2022年 2月 17日
你知道纹影成像可能早于书籍记载吗?在这里,我们通过 CFD 建模探索这一古老的成像技术。

介绍几种计算辐射传热的方法
2022年 2月 10日
跟随我们继续讨论辐射传热建模的基础。 (第 3 部分,共 3 部分)

模拟辐射传热中的入射辐射
2022年 2月 3日
了解如何使用传热模块中的表面对表面辐射接口对表面上的入射辐射进行建模。 (第 2 部分,共 3 部分)
