
该篇博客将简要介绍弱形式,旨在为没接触过有限元分析和矢算、但对弱形式又有浓厚兴趣的用户提供一些物理及积分方面的基础知识。
弱形式简介
对于 COMSOL Multiphysics 的各类物理场,软件都会在后台使用弱公式化来建立数学模型,我们也将它称为弱形式。理解弱形式有助于我们洞察软件的内部工作原理,当模型所涉及的物理场在软件内没有对应的预置接口时,弱形式还可以帮助我们写出自己的方程。
您也许还会对我的同事 Bettina Schieche 所写的另一篇博客感兴趣:”弱形式的优点“。
一个简单示例
现考虑一个无热源的一维稳态热传递案例。我们主要关注 $1\le x\le 5$ 区间内的温度 T,它是位置 x 的函数。简单起见,我们假设导热系数均匀。那么 x 轴正方向的热通量 q 可由温度 T 的梯度给出:
(1)
热通量(域内没有热源)的守恒可简单表示为:
(2)
以上就是需要求解的主要方程。解将给出域内的温度分布。该形式的方程可见于多个学科。例如在静电学中,T 由电势替代,q 由电场替代;在弹性理论中,T 变成位移,q 变成应力。
在此,让我们先来了解为什么 COMSOL Multiphysics 可以轻松求解多物理场耦合问题:不论涉及何种物理机制,它们都会被建模处理成方程;方程确定后,就可以被 COMSOL 软件中的核心算法直接离散和求解。
一些读者可能会好奇我们为什么会选择这么一个过于简单的例子,甚至其解析解都可由非常简单的数学或物理量得到。原因有两个:
- 我们希望专注于弱形式的核心思想,不希望因复杂物理系统中的数学而分散注意力。
- 后续博客中,我们会拓展到涉及多个域的系统,以便阐述两个方程组在边界条件处的耦合。如果现在就开始研究复杂的案例,那等到拓展案例时主题将会变得非常晦涩难懂。
弱公式化
方程 (2) 包含了热通量 q 的一次导数,或者是温度 T 的二次导数,但在温度分布可能受限的实际情况下,这可能导致数值问题。例如,当边界处的相邻材料具有不同导热系数时,温度 T 的一次导数将不连续,进而使温度二阶不可导。弱形式的核心思想是将微分方程变为积分方程,进而减轻数值算法的求导负担。
如希望将微分方程 (2) 变成积分方程,第一步是在 $1\le x\le 5$ 的域上对其积分:
以上方程表示整个域中 $\partial_x q(x)$ 的平均值为零。 的确,与要求 $\partial_x q(x)$ 的值在区间 $1\le x\le 5$ 内全部为零的原始微分方程相比,这显得”太弱”。为了改善该情况,我们可令 $\partial_x q(x)$ 在一个狭小的域内均值为零,假设:
该积分只涉及 x=3.5 附近的 $\partial_x q(x)$ 的值。因此,根据以上关系,其值应约为零:$\partial_x q(3.5) \approx 0$ 。在 $1\le x\le 5$ 的域内所有位置应用这一想法,我们看到原始微分方可以被一组积分方程近似表示,如:
(3)
方程组中积分方程的数量越多,近似效果越好。如果有无限数量的此类积分方程,我们最终能恢复原始的积分方程。写出方程组中所有积分方程十分麻烦,可行性极低,但我们可以用另一种方式来实现这一想法。
主要思想是要在一个狭小范围内对 $\partial_x q(x)$ 取值。通过在方程 (3) 限定的狭小范围内积分,即可实现这一点。同样可以将被积函数乘以一个加权函数 \tilde{T}(x) 来实现同样的取样操作,这在一个狭小范围内也较容易操作,如下图所示:
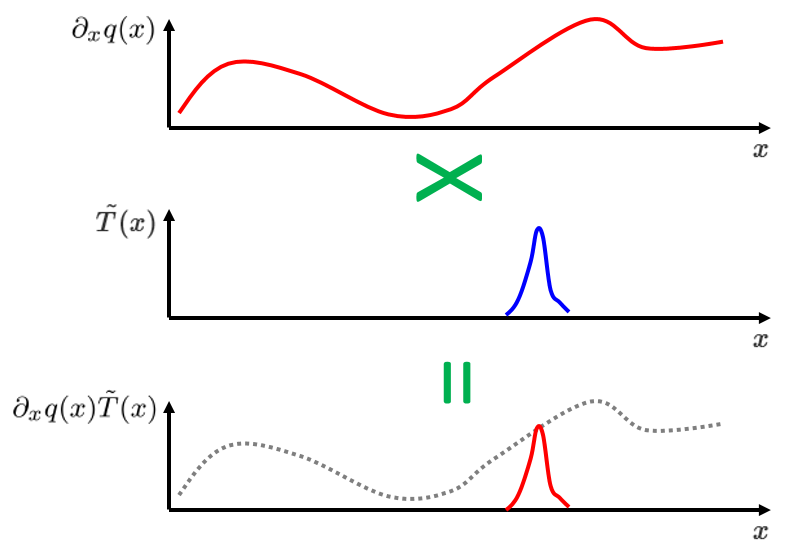
然后,我们可以使用不同的加权函数 \tilde{T}(x) 对 $\partial_x q(x)\tilde{T}(x)$ 在整个域 $1\le x\le 5$ 内积分。每一个加权函数都会把被积函数的贡献项限制在不同 x 值附近的狭小范围内,以此达到方程 (3) 中积分方程组的效果。这样我们获得了弱形式,其表达关系式
(4)
应该满足一组加权函数 \tilde{T}(x),一般称为试函数。对于每一个 x,例如 x=3.5,我们可以选择一个围绕 x=3.5 的加权函数作为试函数 \tilde{T}(x)。将该试函数代入方程 (4) 后会在 x=3.5 附近对$\partial_x q(x)$ 取值,并要求其不应远离零值:$\partial_x q(3.5) \approx 0$。
将大量窄权函数作为试函数代入方程 (4),每一个均围绕区间$1\le x\le 5$ 内的不同位置,域内各处 $\partial_x q(x)$ 的值都会被限制为零。
说明:在上图中,我们有意把 $\partial_x q(x)$ 绘制为任意曲线,而非方程的最终解,意在强调我们还未找到真实的解。在之后的求解过程中,我们将使用一系列的试函数对该任意曲线进行上推或下推,以得出最终解的形状。
降低求导阶数
注意到方程 (4) 中求导阶数和方程 (2) 中相同(毕竟同样都是 $\partial_x q(x)$ 的方程),但是可以用分部积分法来降阶:
(5)
现在,方程和温度 T 中的热通量 q 已不含导数,求导阶数由 2 次降为 1 次。不过方程中的试函数 \tilde{T}(x) 出现了一次导数怎么办?
正如在上一节中所了解到的,试函数是帮我们找出方程解的工具。因此,我们可以选择任意可微形式的试函数。
自然边界条件
方程 (5) 的前两项涉及域边缘 x=1 和 x=5 处的热通量及试函数,热通量 q 定义为沿x-轴正方向。我们可按照离开域的通量进行重写,并将它们移至等号右侧:
(6)
其中 $\Lambda$ 是向外通量,角标 1 和 2 分别表示域边界 x=1 和 x=5。\Lambda_1\equiv -q(x=1) \mbox{, } \Lambda_2\equiv +q(x=5) \mbox{, } \tilde{T}_1\equiv \tilde{T}(x=1) \mbox{, } \tilde{T}_2\equiv \tilde{T}(x=5)。
此外,我们根据热通量关系式 (1),并使用温度 T 及其试函数 \tilde{T} 写出了被积函数。方程的右侧很自然地将边界条件以热通量的形式表示出来。最简单的做法就是将 \Lambda_1 和 \Lambda_2 设为 0,得出绝缘边界条件(即没有热通量经过边界)。
这就是为什么 COMSOL Multiphysics 传热的缺省边界条件是”热绝缘”,固体力学的缺省条件是”自由(无边界力)”,流体流动中是”壁(没有流动经过边界)”。这种明确指出通量或力(求解的第一个导数)的边界条件,一般会被称作 自然边界条件 或是 诺伊曼边界条件。
固定边界条件
另一种边界条件常被称为固定边界条件或是狄利克雷边界条件,它会指明要求解的变量的值。在当前示例中,它指定了边界上一个点的温度值。该边界条件常被用于建立只有唯一解的问题。例如在流体流动中,我们需要明确指定某处的压力(不仅仅是流动);在固体力学中,我们需要明确某处的位移(不仅仅是力)。
如之前的示例所示,弱形式提供了一种很自然的方法来指定边界处的热通量。那么该如何指定边界处的固定温度呢?
技巧如下:利用自然边界条件的数学结构,同时结合试函数并限制解的思路。从概念上讲,要在边界处的某点维持固定温度,就需要用到一个外界的热通量来补偿边界内的热通量。弱公式化将问题表述为:找到在边界一点处维持固定温度所需的热通量。
例如,如果我们希望在 x=1 处将流出通量 \Lambda 指定为 2,在 x=5 处将温度 T 指定为 9,将需引入一个未知变量 \lambda_2 及对应的试函数 \tilde{\lambda}_2,并将方程 (6) 写成:
(7)
这里,等号右侧的第一项指定 x=1 处的向外通量为 2,第二项指定 x=5 处的未知通量;两项均由方程 (6) 右侧的自然边界条件项求得。
新的变量 \lambda_2 表示在边界 x=5 处的未知通量 。方程中的第三项采用了与之前讨论试函数 \tilde{T}(x) 时相同的方法,即使用试函数 \tilde{\lambda}_2 保证在 x=5 处解为T=9。
对于更高维度的考虑
到目前为止,我们一直在讨论非常简单的一维示例。在更高的维度中,例如二维平面域或是三维体域,方程将更为复杂,但基本思路相同。
弱形式将微分方程变为积分方程。分部积分对导数进行降阶从而减轻计算负担,并产生自然边界条件以明确边界处的通量。在简单的一维示例中,边界是两个端点,通量是每点处的单一值。
在二维和三维中,边界分别是闭合曲线和包围域的闭合面。方程 (6) 的右侧变成流入通量密度的线或面积分,即总流入通量。本质上,二维和三维的分部积分过程使用了 散度定理 来得到模型域内边界处通量的线或面积分。
在本篇博客中我们选择了一个简单的一维示例,旨在保证弱形式的核心思路不会被数学的复杂性所掩盖。
总结及下一篇博客
今天我们学习了使用试函数对解进行降阶的弱公式化方法。对弱形式进行分部积分利于降低求导阶数。同时也提供了一种以通量或力(求解变量的一次导数)指定边界条件的自然方法,即自然边界条件或诺伊曼边界条件。
求解实际问题时,通常需要使用我们所称的固定边界条件或是狄利克雷边界条件来指定要求解的变量,而非仅只是指定它的导数。我们看到在为固定边界条件构建附加项时,弱形式使用了与试函数及自然边界条件相同的机制。
至此,我们一直使用的是方程的原始解析形式,没有对它进行任何数值近似。在下一篇博客中,我们会在 COMSOL Multiphysics 中对弱形式方程 (7) 进行数值求解。之后,我们将会讨论数值近似值是如何在软件内部求得的,同样的问题如何以不同的方式求解,以及如何为不同类型的问题设定不同的边界条件。



评论 (13)
峰 程
2016-04-06Dear Chien,
Thanks for your article. I have some questions about it.
First, I can’t understand the derivation of Eq.(4). I think Eq.(4) should be written as
[int_1^5 {{partial _x}qleft( x right)delta left( {x – y} right)} dx = 0]
with
[1 le y le 5].
Here I used the Dirac delta function to replace the test function. It can be replaced by other “narrow” functions, but its strictness will be “weakened”.
Can you tell me a little more about the test function so I can relate it with the Dirac delta function?
Many thanks.
Sincerely,
Feng
Chien Liu
2016-04-07 COMSOL 员工Dear Feng,
It will become clear later in this blog:
https://www.comsol.com/blogs/discretizing-the-weak-form-equations/
why the Dirac delta function would not be a good choice as the test function for numerical analysis. Roughly speaking we need the basis function to have some finite width in order to reconstruct the solution function. For more in-depth discussion on this topic, you may want to take a look at the references listed in the comments of this blog:
https://www.comsol.com/blogs/implementing-the-weak-form-in-comsol-multiphysics/
Sincerely,
Chien
峰 程
2016-04-08刘老师好,
看了您后续的几篇博客感觉豁然开朗。目前还有一个小问题,公式(7)中的lamda2是怎么引入的?
谢谢。
Chien Liu
2016-04-12 COMSOL 员工Dear 峰 程,
You can think of lambda2 as the heat flux needed to keep the boundary temperature T2 at the specified value of 9. So here we are instructing the software to “adjust the value of the heat flux lambda2 at the boundary, until the boundary temperature T2 reaches the value of 9”. Does this make sense?
Sincerely,
Chien
zidong song
2017-07-19刘老师好,
请问弱形式偏微分方程模块中周期性条件为什么没有Floquet类型,如果要是自己设置的话该如何设置呢?
谢谢!
宇航 秦
2017-07-21Song Zidong, 您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
梓鹏 梁
2018-07-26刘老师好,
请问为什么方程7中右面第三引入项是lambda2对应试函数与(T2-9)的乘积?lambda2的试函数是如何保证在x=5处T=9的?
Chien Liu
2018-07-26 COMSOL 员工Dear 梓鹏, Thank you for the question. One way to think about this is to consider a problem of constrained optimization. Then the last two terms in equation 7 come from taking the variation operation on the product of the Lagrange multiplier (labmda_2) and the constraint (T_2-9). Sincerely, Chien
稳军 赵
2022-11-01方程(7)右边第二项不应该是 q(x=5)*test(T2) 吗 ?
为什么变成 λ2*test(T2) 了?
q为什么变成λ2了?
Qihang Lin
2022-11-02 COMSOL 员工请注意文中表述的边界条件希望是:在x=1处指定 “通量” 为2,在x=5处指定 “温度” 为 9,在两个位置指定的边界条件存在一个一阶求导差别。因此(7)式的第一项为与(6)式类似指定了通量-2*test(T1),而后两项应当归类为同一项进行理解,即:首先我们需要令 x=5 处的温度等于 9,所以写入了第三项-test(lamda2)*(T2-9)。而由于指定了一个温度边界条件会引起通量不一定守恒,于是按照自然边界理论此处应当加一个未知的待求通量项 -lamda2*test(T2) 使整个方程如(6)式一样守恒。希望通过以上解释能够让您顺利理解该博客的公式推导。
稳军 赵
2022-11-05感谢您的回复,我再想想
Zhengyu Shi
2023-06-12您好,请问下 “我们需要令 x=5 处的温度等于 9,所以写入了第三项-test(lamda2)*(T2-9)” 这个表达式前面的负号有什么意义吗?
明森 谭
2023-04-17老师好,请问弱形式的初值怎么设置。比如我仿真光电导天线,其中半导体模块的初值由电磁波频域模块的结果所赋予,那如果对半导体模块使用弱形式方程,请问初值该怎么设置?