
在涉及共轭传热的许多工程应用中(例如,换热器和散热器设计),传热系数的计算很重要。我们经常通过相关性和经验关系来确定传热系数,以获得固体和流体之间的信息。在本篇博客文章中,我们将讨论并演示如何使用 COMSOL Multiphysics® 软件求解平板几何的传热系数。
什么是传热系数?
下面,让我们以在加热壁或表面上流动的流体为例,说明传热系数的含义。流体中的传热主要由对流控制。类似地,当流动的流体(流经固体表面)有两种时,其主要的传热方式也是对流,例如热交换器。在这两种情况下,传热速率均由温差和一个被称为传热系数 的比例系数决定。传热系数表明了通过表面和流体之间某个域的有效的传热速率。
在数学上,传热系数 h 可以表示为壁上的热通量与壁和流体之间的温差之比。即
(1)
其中,q^{\prime \prime} 是热通量, T_w 是壁的温度,T_\infty 是流体特征温度。
流体特征温度也可以是远离壁的外部温度或管中的本体温度。
当物体被无限大体积的空气包围时,我们假设远离物体的空气温度是一个恒定的已知值。在这种情况下计算的传热系数称为外部传热系数。
根据上述假设,如果我们仔细观察近壁处(如果在y方向上定义了壁的厚度,并且 y=0 代表壁的表面/平面),那么很明显,壁面上的无滑移条件会形成一层停滞的流体薄膜。因此,通过紧邻壁面的流体传热完全是依靠热传导进行的。
传递的热量可以用以下数学公式(参考资料1)表示:
(2)
其中,k 是流体的热导率,T 是在流体中计算的导数。
(3)
\bigg)_{y=0}}{T_w {-} T_\infty}
在 COMSOL Multiphysics® 中计算传热系数
实际上,壁上的温度梯度很难测量。此外,采用一种智能且计算成本低的分析方法来理解壁上的传热至关重要。因此,我们通常首选使用非解析的方法来计算传热系数。
一种常用的方法是使用由无量纲的努塞尔数定义的对流相关性。这些相关性适用于各种情况,包括自然对流和强制对流以及内部和外部流动,并能快速得到结果。但是,此方法只能用于规则的几何形状,例如水平和垂直的壁、圆柱体和球体。
当涉及复杂形状时,我们可以通过模拟共轭传热现象来计算传热系数。
现在我们讨论两种不同的情况和方法:
- 使用以下方法计算规则几何(如水平板)中的传热系数:
- 共轭传热分析
- 对流相关性;即,不考虑流动
- 计算不规则/复杂几何形状(如波纹板)中的传热系数
注意,因为传热系数取决于速度,所以流态是重要的考虑因素。在以下两种情况中,例如鼓风机系统或电子芯片冷却设备中的快速流动,都需要考虑实际情况。这表明有必要将传热与湍流进行耦合建模。
示例1:强制对流和流过水平板的流体
以模拟流经长度为 5m 的水平平板为例,该平板受到恒定且均匀的 10 W/m2 的热通量。将板放置在平均速度为 0.5m/s,温度为 283K 的气流中。下图为描述该问题的示意图,分别包含动量边界层(例如,\delta )和热边界层(\delta_{T})的速度和温度场。
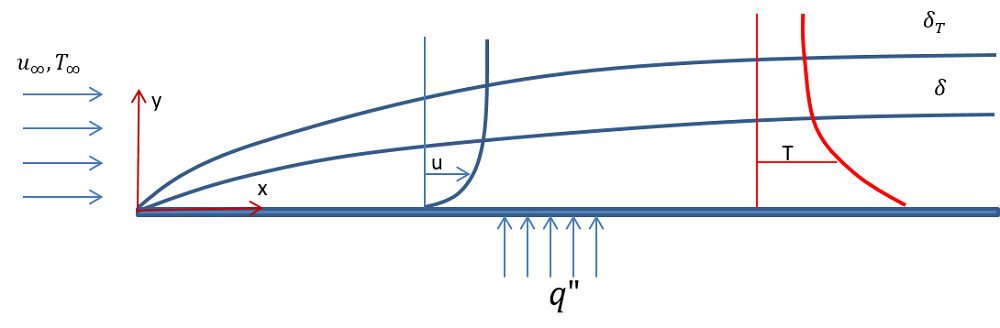
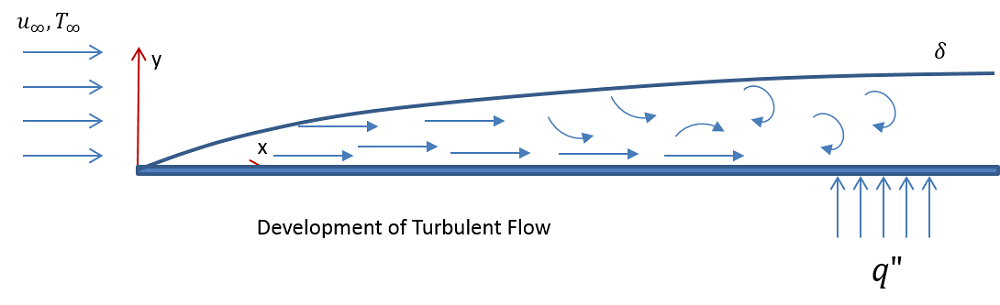
通过水平平板的层流(顶部)和湍流(底部)的示意图。
共轭传热分析
我们可以使用COMSOL Multiphysics 中的共轭传热 接口获得数值解,该接口耦合了流体流动和传热现象。在空气域中计算速度场和压力,在板和空气域中计算温度。
下图显示了板和流体内部的温度分布。在从壁到板上方 2cm 的域中可以看到在流体域内部形成的热边界层和动量边界层。
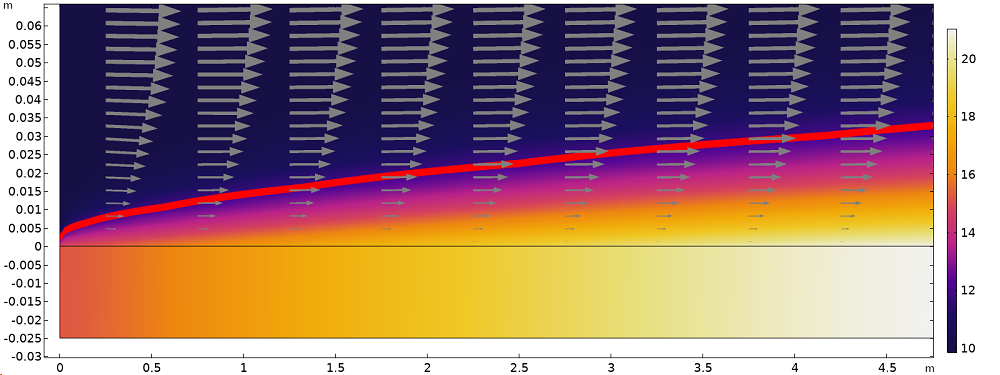
温度分布(表面图),11°C 时的等温线(红线)和速度场(箭头),说明了靠近板表面的热边界层和动量边界层(各向异性轴比例)。
根据仿真结果,可以使用相应的预定义后处理变量计算热通量。除以温差 (T_w-T_\infty) 得到传热系数(等式3)。通过共轭传热分析获得的沿板传热系数将在下一节的图中绘制。
基于努塞尔数相关性的传热系数
我们使用文献中提供的通过平板的强制对流的努塞尔数相关性(例如,参考文献1)。
在该方法中,求解的是相同的模型但无需求解流动,而是使用传热相关性。计算域被限制在固体(板)内,使用热通量 边界条件定义从热板到冷流体的热损耗。如下图所示,该边界条件包含一个使用预定义的努塞尔数相关性定义传热系数的选项。请注意,此相关性是在 COMSOL Multiphysics 中预定义的。
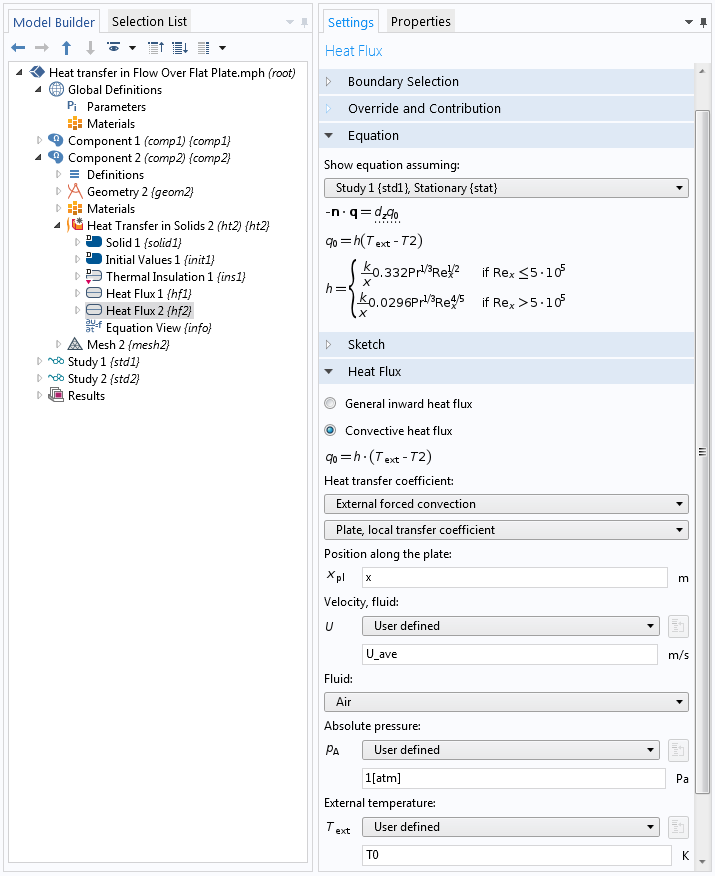
设置 热通量边界条件。
仅使用这种方法,就可以计算板中的温度分布。根据在热通量边界条件中定义的传热系数,我们可以计算板表面的热通量,q=h\cdot(T_\infty-T)。
计算传热系数
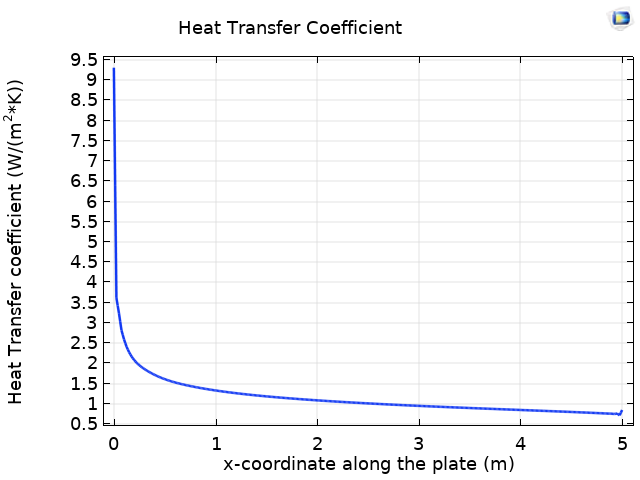
采用上述两种方法,都可以计算沿平板的传热系数。下图比较了使用两种方法计算的传热系数。
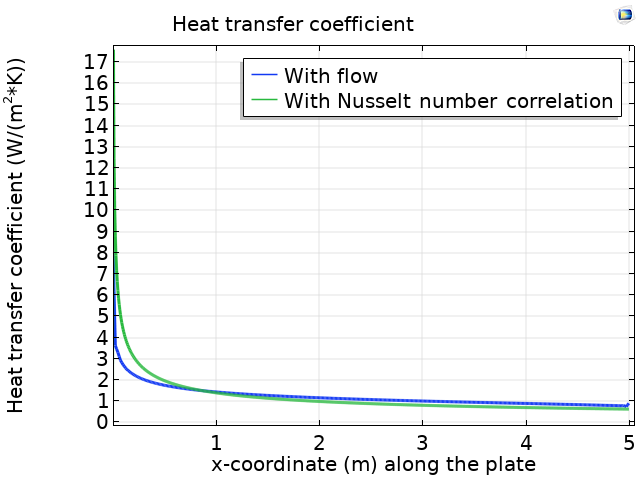
使用共轭传热仿真(蓝线)和努塞尔相关性(绿线)计算的沿平板的传热系数的比较。
我们可以看到,从努塞尔数相关性获得的值与从完全共轭传热模拟获得的值非常吻合。
在这两种情况下,单位厚度壁上的热通量分别为:
- 努塞尔数相关性:50W/m
- 共轭传热:884W/m
对于某些计算,基于努塞尔数相关性的方法能够准确的预测热通量。接下来,我们研究一种不规则形状的情况。在这种情况下,努塞尔数相关性不容易获得,唯一可行的方法是进行共轭传热仿真。
示例2:流经波纹水平板的流体
接下来,以与第一种情况条件类似,唯一的区别是上表面是波纹状的板为例。下图为描述该问题的示意图。在此模型中,仅在模型几何的一个部分考虑了板平面的波纹,其余部分为平板。
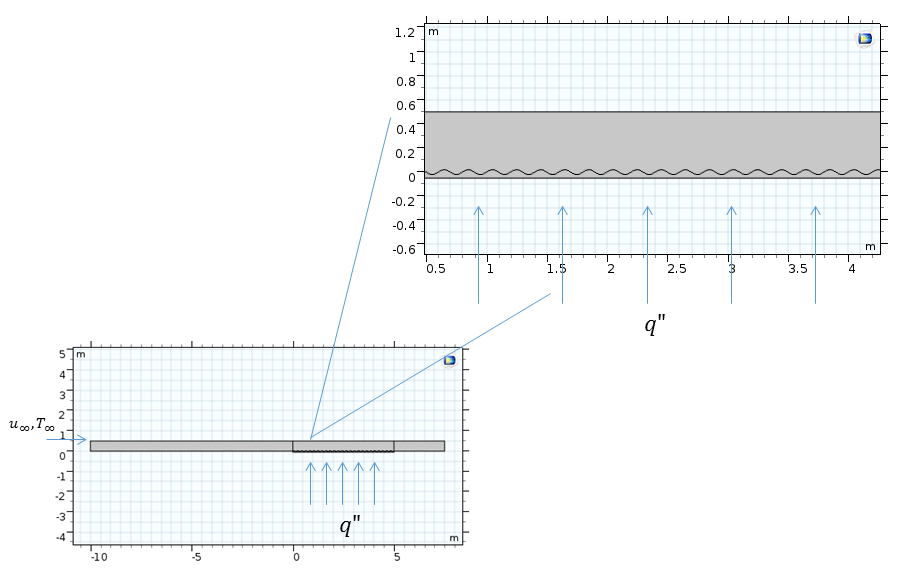
流经水平板的示意图。
图中,靠近壁的流场具有提高传热速率的回流区。在下图中,我们可以看到温度分布和速度流线。
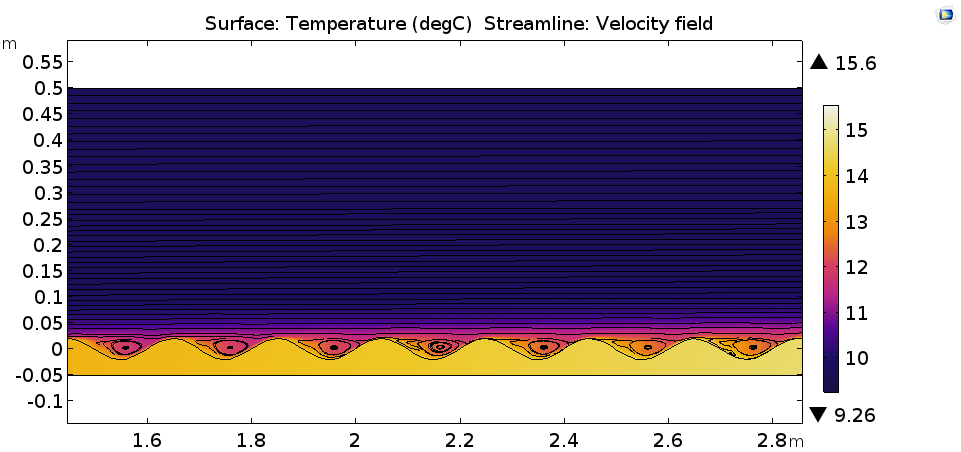
温度分布(摄氏度,表面)和速度场(流线)。
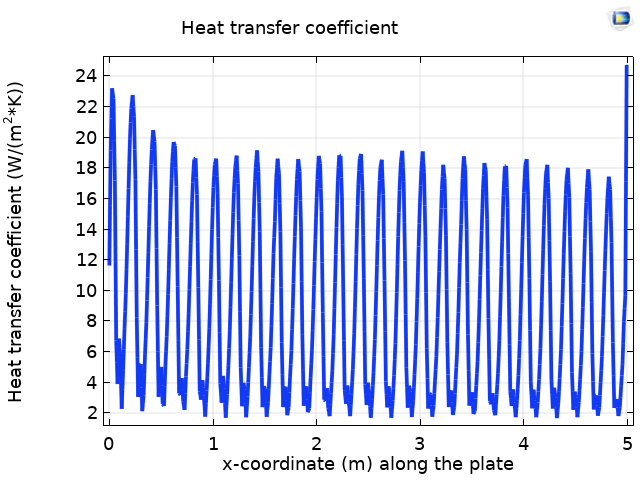
下方左图显示了沿波纹板长度的传热系数。对于波浪形板的几何形状,传热系数取决于温度场、速度场和波纹的几何参数(例如高度)。因此,优下方右图,我们可以发现与平板相比增大的传热系数。
沿波纹板(左)和沿平板(右)的传热系数。
对于包含波纹表面的复杂几何形状,共轭传热方法的计算成本可能很高,所以需要寻找替代方法。一个很好的近似方法是:我们可以假设表面无波纹来降低几何复杂度,并从波纹板的几何形状推断出传热系数,同时考虑诸如波纹高度、流速场和表面温度变化等几何参数。
为了验证结果,我们以一个简单的情况为例,其中传热系数是在波纹板几何形状的整个速度场中计算的。由该数据可获取平均传热系数,并可扩展用于平板几何模型。为了了解这种近似的有效性,我们可以研究表面的总热损耗或从包含流动的仿真中获得传热系数。
结论
在本篇博客文章中,我们介绍了使用两种方法计算传热系数的示例。有了共轭传热结果,我们就可以使用 COMSOL Multiphysics 中提供的内置热通量变量。使用带有努塞尔数相关性的热通量边界条件,我们可以模拟涉及简单形状的问题。另外,我们还讨论了如何降低几何复杂度以获得复杂几何形状的传热系数。
后续操作
单击下面的按钮,了解有关在 COMSOL® 软件中进行传热建模的特殊功能的更多信息。
尝试以下教程中讨论的方法:
参考
- A. Bejan et al., Heat Transfer Handbook, John Wiley & Sons, 2003.




评论 (2)
Lanny Liang
2023-06-30I want to kindly ask about what expression you used for evaluating HTC on convective surfaces in postprocessing?
Yi Li
2023-07-18 COMSOL 员工h = q/(Tw-T∞), where q is the heat flux, Tw is the wall temperature, and T∞ is the characteristic fluid temperature.
The specific expressions used in the postprocessing you can find in the following example:
https://cn.comsol.com/model/nonisothermal-turbulent-flow-over-a-flat-plate-56591